Hướng dẫn:

Ta có:

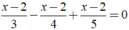
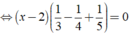
⇔ ( x - 2 )17/60 = 0 ⇔ x - 2 = 0 ⇔ x = 2.

Vậy phương trình có tập nghiệm là S = { 2 }.

(x+1).(x+2).(x+3).(x+4) - 24 = 0

(x² + 5x + 4).(x² + 5x + 6) - 24 = 0

(x² + 5x + 5-1).(x² + 5x + 5 + 1) - 24 = 0

(x² + 5x + 5)² - 1  - 24 = 0

(x² + 5x + 5 - 5).(x² + 5x + 5 + 5) = 0

x.(x+5) .(x² + 5x + 10) = 0

=> x = 0

x+ 5 = 0 => x = -5

\(x^2+5x+10>0\)

KL:..

    (x+1)(x+2)(x+3)(x+4) - 24 = 0

<=> [(x+1)(x+4)][(x+2)(x+3)] - 24 =0

<=> (x^2+4x+x+4)(x^2+3x+2x+6) - 24 = 0

<=> (x^2+5x+4)(x^2+5x+6) - 24 = 0

  Đặt x^2+5x+5 = a, ta có

       (a-1)(a+1) - 24 = 0

<=> a^2 - 1 - 24 = 0

<=> a^2 - 25 =0

<=> a = 5

hay x^2 + 5x + 5 = 5

<=> x(x+5) = 5 - 5 = 0

<=> x=0      hoặc   x+5 = 0 <=> x= -5

   Vậy tập ngh của p.tr là S = { 0; -5 }

(x + 2)(x + 3)(x + 4)(x + 5) - 24 = 02

\(\Leftrightarrow\) [(x + 2)(x + 5)][(x + 3)(x + 4)] - 24 = 0

\(\Leftrightarrow\) (x² + 7x + 10)(x² + 7x + 12) - 24 = 0

Đặt x² + 7x + 11 = a. Thay vào ta có :

(a - 1)(a + 1) - 24 = 0

\(\Leftrightarrow\) a² - 25 = 0

\(\Leftrightarrow\) (a - 5)(a + 5) = 0

\(\Leftrightarrow\left[{}\begin{matrix}a-5=0\\a+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=5\\a=-5\end{matrix}\right.\)

TH1 : a = 5

\(\Leftrightarrow\) x² + 7x + 11 = 5

\(\Leftrightarrow\) x² + 7x + 6 = 0

\(\Leftrightarrow\) (x + 1)(x + 6) = 0

\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x+6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-6\end{matrix}\right.\)

TH2 : x² + 7x + 11 = -5

\(\Leftrightarrow\) x² + 7x + 16 = 0

\(\Leftrightarrow\) (x² + 2.\(\frac{7}{2}\).x + \(\frac{49}{4}\)) + \(\frac{15}{4}\) = 0

\(\Leftrightarrow\) (x + \(\frac{7}{2}\))² + \(\frac{15}{4}\) = 0 mà \(\left(x+\frac{7}{2}\right)^2\ge0\) \(\Rightarrow\) Vô lý

Vậy S = \(\left\{-1,-6\right\}\)

\(\Leftrightarrow\left(x^2+5x+4\right)\left(x^2+5x+6\right)-24=0\)

\(Đặt\) \(t=x^2+5x+5\). PT thành

\(\left(t-1\right)\left(t+1\right)-24=0\Leftrightarrow t^2-25=0\Leftrightarrow\left(t-5\right)\left(t+5\right)=0\Rightarrow\left[{}\begin{matrix}x^2+5x+5=5\\x^2+5x+5=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x\left(x+5\right)=0\\\left(x+\frac{5}{2}\right)^2+\frac{15}{4}>0\end{matrix}\right.\)

Vậy x=0 hoặc x=-5

(x² + 7x)² - 2(x² + 7x) - 24 = 0

<=> (x² + 7x)(x² + 7x - 2) - 24 = 0 (1)

Đặt t = x² + 7x - 1 = \(=\left(x+\frac{7}{2}\right)^2-\frac{53}{4}\)

(1) trở thành (t + 1)(t - 1) - 24 = 0

<=> t² - 1 - 24 = 0

<=> t² - 25 = 0

<=> t² = 25

<=> t = 5 hoặc t = -5

+) t =\(\left(x+\frac{7}{2}\right)^2-\frac{53}{4}\) = 5

\(\Leftrightarrow\left(x+\frac{7}{2}\right)^2=\frac{73}{4}\)

\(\Leftrightarrow x=\frac{-7+\sqrt{73}}{2};x=\frac{-7-\sqrt{73}}{2}\)

+) t = \(\left(x+\frac{7}{2}\right)^2-\frac{53}{4}=-5\)

\(\Leftrightarrow\left(x+\frac{7}{2}\right)^2=\frac{33}{4}\)

\(\Leftrightarrow x=\frac{-7+\sqrt{33}}{2};x=\frac{-7-\sqrt{33}}{2}\)

Vậy ...

1. Ta có \(\left(x+2\right)\left(x+4\right)\left(x+6\right)\left(x+8\right)+16=0\)

\(\Rightarrow\)\(\left[\left(x+2\right)\left(x+8\right)\right].\left[\left(x+4\right)\left(x+6\right)\right]+16=0\)

\(\Rightarrow\left(x^2+10x+16\right)\left(x^2+10x+24\right)+16=0\)

Đặt \(x^2+10x=t\)

Pt \(\Leftrightarrow\left(t+16\right)\left(t+24\right)+16=0\Leftrightarrow t^2+40t+400=0\Leftrightarrow t=-20\)

\(\Rightarrow x^2+10x+20=0\Rightarrow\orbr{\begin{cases}x=-5+\sqrt{5}\\x=-5-\sqrt{5}\end{cases}}\)

2. Ta có \(\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)-24=0\)

\(\Rightarrow\left[\left(x+2\right)\left(x+5\right)\right].\left[\left(x+3\right)\left(x+4\right)\right]-24=0\)\(\Rightarrow\left(x^2+7x+10\right)\left(x^2+7x+12\right)-24=0\)

Đặt \(x^2+7x=t\Rightarrow\left(t+10\right)\left(t+12\right)-24=0\Rightarrow t^2+22t+96=0\)\(\Rightarrow\orbr{\begin{cases}t=-6\\t=-16\end{cases}}\)

Với \(t=-6\Rightarrow x^2+7x+6=0\Rightarrow\orbr{\begin{cases}x=-6\\x=-1\end{cases}}\)

Với \(t=-16\Rightarrow x^2+7x+16=0\left(l\right)\)

Vậy pt có 2 nghiệm là \(\orbr{\begin{cases}x=-6\\x=-1\end{cases}}\)

Quản lí Hoàng Thị Lan Hương giúp em giải bài toán vừa đăng lên đc ko ạ.??? ^^

Đặt x² + 10x + 24 = y

pt đã cho trở thành ( y + 4x ).y - 165x² = 0

<=> y² + 4xy - 165x² = 0

<=> y² - 11xy + 15xy - 165x² = 0

<=> y( y - 11x ) + 15x( y - 11x ) = 0

<=> ( y - 11x )( y + 15x ) = 0

=> ( x² + 10x + 24 - 11x )( x² + 10x + 24 + 15x ) = 0

<=> ( x² - x + 24 )( x² + 25x + 24 ) = 0

<=> ( x² - x + 24 )( x² + 24x + x + 24 ) = 0

<=> ( x² - x + 24 )[ x( x + 24 ) + ( x + 24 ) ] = 0

<=> ( x² - x + 24 )( x + 24 )( x + 1 ) = 0

Vì x² - x + 24 > 0 ∀ x

nên pt <=> ( x + 24 )( x + 1 ) = 0 <=> x = -24 hoặc x = -1

Vậy ...

Đặt t = \(x^2+14x+24\)

\(\Rightarrow\)\(t\left(t-4x\right)-165x^{^2}=0\)

\(\Leftrightarrow t^2-4xt-165x^2=0\)

\(\Leftrightarrow t^2+11xt-15xt-165x^2=0\)

\(\Leftrightarrow t\left(t+11x\right)-15x\left(t+11x\right)=0\)

\(\Leftrightarrow\left(t+11x\right)\left(t-15x\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}t+11x=0\\t-15x=0\end{cases}\Leftrightarrow\orbr{\begin{cases}t=-11x\\t=15x\end{cases}}}\)

với t= -11x

\(\Rightarrow x^2+14x+24=-11x\)

\(\Leftrightarrow x^2+25x+24=0\)

\(\Leftrightarrow x^2+x+24x+24=0\)

\(\Leftrightarrow x\left(x+1\right)+24\left(x+1\right)=0\)

\(\Leftrightarrow\left(x+1\right)\left(x+24\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x+1=0\\x+24=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-1\\x=-24\end{cases}}}\)

với t=15x

\(\Rightarrow x^2+14x+24=15x\)

\(\Leftrightarrow x^2-x+24=0\)

\(\Leftrightarrow\left(x-\frac{1}{2}\right)^2+\frac{95}{4}=0\)(Vô Lí)

vậy....