cho hình vuông ABCD cạnh a . M thuộc AB
a,Mlaf trung điểm của AB tính trị tuyệt đối của 5MA→+MB→+MC→
b,Mthuoocj đoạn AB. tìm mã của trị đối của 3MA→+MB→+MC→+MD→

Những câu hỏi liên quan
Cho tam giác ABC gọi M là trung điểm của cạnh BC trên tia đối của tia MA lấy điểm D sao cho MD = MA A CM AB=CD AC VUÔNG GÓC DC B CM MA=MB=MC C KẺ AH VUÔNG GÓC BC TẠI H CM AH<=BC/2
cho tam giác ABC, điểm D thuộc cạnh BC. Gọi M là trung điểm AB trên tia đối của tia MB ấy điểm E sao cho ME=MB. Trên tia đối của tia MC lấy điểm F sao cho MF=MC. Chứng minh
a) AE=BD
b) AF \(//\)BC
C) 3 điểm A E F thẳng hàng
Câu hỏi của Tuấn Anh Nguyễn - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo link bài làm tương tự nhé!
Đúng 0
Bình luận (0)
cho tứ giác ABCD và điểm M thuộc đường trong của tứ giác
Chứng minh : a) MA+MB+MC+MD > AB+CD
b) MA+MB+MC+MD \(\ge\dfrac{AB+BC+CD+DA}{2}\)
Hình bạn tự vẽ nhé.
a) Theo bất đẳng thức tam giác:
MA+MB> AB (1)
MC+MD>CD (2)
=> MA +MB +MC +MD >AB +CD
b) Theo BĐT tam giác:
MA+MD > AD (3)
MB +MC >BC (4)
(1)(2)(3)(4) => 2(MA +MB+MC+MD)>AB +BC +CD +AD
MA +MB +MC +MD>AB +BC +CD +AD /2
Mình không nghĩ là dấu≥ vì bất đẳng thức tam giác đâu có dấu bằng đâu nhỉ?
Đúng 1
Bình luận (2)
cho tam giác ABC M là trung điểm của AC.N là trung điểm của AB trên tia đối của tia MB lấy điểm D.trên tia đối của tia MC lấy E sao cho MB=MD,NC=NE.Chứng minh a.AD=AEb.A,E,D thẳng hàng
cho tam giác ABC có A(1 , 2) , B(-2 , 6) , C(9 , 8) . Tìm tập hợp điểm M thỏa mãn : 3 nhân giá trị tuyệt đối của ( vector MA + vector MB ) = 2 nhân giá trị tuyệt đối của ( vector MA + vector MB + vector MC )
Gọi M(x,y) là điểm cần tìm
\(\overrightarrow{MA}+\overrightarrow{MB}=(-1-2x;8-2y)\)
\(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=(8-3x;16-3y)\)
Theo giả thiết \(3|\overrightarrow{MA}+\overrightarrow{MB}|=2|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}|\), suy ra
\(3\sqrt{(-1-2x)^2+(8-2y)^2}=2\sqrt{(8-3x)^2+(16-3y)^2}\)
\(\Leftrightarrow 9(4x^2+4y^2+4x-32y+65)=4(9x^2+9y^2-48x-96y+320)\)
\(\Leftrightarrow 228x+96y-695=0\)
Vậy tập các điểm M cần tìm là đường thẳng 228x+96y-695=0
Đúng 0
Bình luận (0)
Em thật sự ko biết làm nhưng thật sự em lại biết làm!!![]()
![]()
![]()
![]()
Đúng 0
Bình luận (0)
Cho nửa đường tròn đường kính AB. Gọi M là điểm chính giữa của cung AB. Trên cung AM lấy điểm N. Trên tia đổi của tia MA lây điểm D sao cho MD = MB, trên tia đối của tia NB lấy điểm E sao cho NA = NE, trên tia đối của tia MB lấy điểm c sao cho MC = MA. Chứng minh 5 điểm A, B, C, D, E cùng thuộc một đường tròn
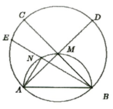
Các tam giác ∆ANE, ∆AMC và ∆BMD vuông cân
=> A E B ^ = A D B ^ = A C B ^ = 45 0
Mà AB cố định nên các điểm A, B, C, D, E cùng thuộc một đường tròn
Đúng 0
Bình luận (0)
trên tia phân giác góc A của tam giác ABC(AB>AC) lấy điểm M.Chứng Minh:
giá trị tuyệt đối MB-MC< AB-AC
Trên AB lấy D sao cho AD=AC =>AB-AC=BD(1)
Nối M và D
Xét tam giác AMC và AMD
góc CAM=MAD
AM chung AC=AD
=>Tam giác AMC=AMD
=>CM=MD(......)(2)
Xét tam giác MDB
MB-MD<DB( BĐT tam giác)(3)
Thay1;2 vào 3
Ta được MB-MC< AB-AC
Đúng 0
Bình luận (0)
Trên cạnh AB lấy điểm E sao cho AE=AC
Xét tam giác ACM và tam giác AEM có:
AM chung
góc CAM=góc EAM(AM là tia p/g của góc A)
AC=AE(cách vẽ)
=>tam giác ACM và tam giác AEM(c-g-c)
=>CM=EM(2 cạnh tương ứng)
Xét tam giác NEB có:MB-ME<EB(BĐT tam giác)
Mà MC=ME(cmt)
=>MB-MC<EB (1)
Ta có:AC=AE(cách vẽ)
Mà AB-AE=EB
=>AB-AC=EB (2)
Từ (1) và (2) =>MB-MC<AB-AC
Hay |MB-MC|<AB-AC (đpcm)
Cho tứ diện ABCD có O là trung điểm của đoạn thẳng nối trung điểm của hai cạnh đối diện và a là số thực dương không đổi. Tập hợp các điểm M trong không gian thỏa mãn hệ thức
M
A
→
+
M
B
→
+
M
C...
Đọc tiếp
Cho tứ diện ABCD có O là trung điểm của đoạn thẳng nối trung điểm của hai cạnh đối diện và a là số thực dương không đổi. Tập hợp các điểm M trong không gian thỏa mãn hệ thức M A → + M B → + M C → + M D → = a là
A. mặt cầu tâm O bán kính r = a 3 .
B. mặt cầu tâm O bán kính r = a 4 .
C. mặt cầu tâm O bán kính r = a .
D. mặt cầu tâm O bán kính r = a 2 .
Đáp án B
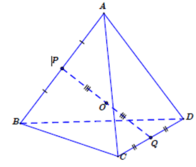
* Gọi P, Q lần lượt là trung điểm của AB, CD. Theo giả thiết O là trung điểm của PQ nên suy ra O là trọng tâm của tứ diện ABCD.
M A → + M B → + M C → + M D → = a
⇔ 4 O M → = a ⇔ O M = a 4
Vậy tập hợp các điểm M trong không gian là mặt cầu tâm O bán kính r = a 4
Đúng 0
Bình luận (0)
Cho tam giác abc vuông tại a ( AB<AC) M là trung điểm của AB. Trên tia đối của tia MC lấy điểm D sao cho : MD=MC . C/m : a) tam giác AMD = tam giác BMC b)BD vuông góc với AB c) Gọi N là trung điểm của BC , trên tia đối của tia NA lấy điểm E sao cho NE = NA chứng minh D,B,E thẳng hàng
a/ Xét t/g AMD và t/g BMC có
AM = BM (M là TĐ AB)
\(\widehat{AMD}=\widehat{BMC}\) (đối đỉnh) MD = MC (GT)
=> t/g AMD = t/g BMC (c.g.c)
b/ Xets t/g BMD và t/g AMC có
BM = AM
\(\widehat{BMD}=\widehat{AMC}\)(đối đỉnh) MD = MC (GT)
=> t/g BMD = t/g AMC (c.g.c)
=> \(\widehat{ABD}=\widehat{BAC}=90^o\)
=> BD ⊥ AB (1)
c/ Xét t/g BNE và t/g CNA có
BN = CN (N là TĐ BC)
\(\widehat{BNE}=\widehat{CNA}\) (đối đỉnh) NE = NA (GT)
=> T/g BNE = t/g CNA (c.g.c)
=> \(\widehat{EBN}=\widehat{CAB}=90^o\) (2 góc t/ứ)
=> BE ⊥ AB (2) Từ (1) và (2)
=> D , B , E thẳng hàng
Đúng 0
Bình luận (0)




















