a)log2x+1(3-x2)=2
b)log2(5-2x)=2-x
c)log2(x+1)=4-3x
Những câu hỏi liên quan
Nghiệm của phương trình log 2 x = log 2 ( x 2 − 2 x − 4 ) là
A. x = -1
B. x = 3
C. x = 4
D. x = -1 hoặc x = 4
Xét các mệnh đề sau (1) log2(x - 1)2 + 2log2(x+1) 6 2log2(x-1) + 2log2(x+1) 6 (2) log2(x2+1)
≥
1 + log2|x|;
∀
x
∈
R
(3) xlny ylnx;
∀
x
y
2
(
4
)
log
2
2
2
x
-
4
log...
Đọc tiếp
Xét các mệnh đề sau
(1) log2(x - 1)2 + 2log2(x+1) = 6
<=> 2log2(x-1) + 2log2(x+1) = 6
(2) log2(x2+1) ≥ 1 + log2|x|; ∀ x ∈ R
(3) xlny = ylnx; ∀ x > y > 2
( 4 ) log 2 2 2 x - 4 log 2 x - 4 = 0 ⇔ log 2 2 x - 4 log 2 x - 3 = 0
Số mệnh đề đúng là
A. 0
B. 1
C. 2
D. 3
Đáp án C
Dựa vào giả thiết, ta thấy rằng:
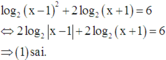
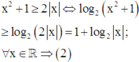
đúng.
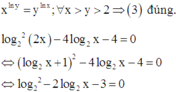
=> (4) sai. Vậy có 2 mệnh đề đúng.
Đúng 0
Bình luận (0)
4 tháng 10 2021 lúc 22:33
Tính tổng tất cả các nghiệm của phương trình: \(\dfrac{1}{2}\).log2(x+3) = log2(x+1) + x2 - x - 4 + 2\(\sqrt{x+3}\)
ĐKXĐ: \(x>-1\)
Bước quan trọng nhất là tách hàm
\(\Leftrightarrow log_2\sqrt{x+3}-2\sqrt{x+3}+\left(x+3\right)=log_2\left(x+1\right)-2\left(x+1\right)+\left(x+1\right)^2\)
Đến đây coi như xong \(\Rightarrow\sqrt{x+3}=x+1\Rightarrow x=1\)
Đúng 1
Bình luận (0)
Cho các số thực x,y dương thỏa mãn
log
2
(
x
+
2
y
)
2
log
2
x
+...
Đọc tiếp
Cho các số thực x,y dương thỏa mãn log 2 ( x + 2 y ) 2 = log 2 x + 4 log 4 y . Giá trị nhỏ nhất của biểu thức P = x 2 ( 1 + 4 y + 4 y 2 2 x + 1 bằng
A. 4.
B. 32/9.
C. 37/9.
D. 10/3
Cho hàm số
y
ln
(
2
x
-
a
)
-
2
m
ln
(
2
x
-
a
)
+...
Đọc tiếp
Cho hàm số y = ln ( 2 x - a ) - 2 m ln ( 2 x - a ) + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 ( x 2 + a 2 ) + log 2 ( x 2 + a 2 ) + log 2 ( x 2 + a 2 ) + . . . + log . . . 2 ( x 2 + a 2 ) - ( 2 n + 1 - 1 ) ( log 2 x a + 1 ) = 0
(với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thoả mãn m a x [ 1 ; e 2 ] y = 1 . Số phần tử của S là
A. 0
B. 1
C. 2
D. Vô số
Cho x, y là số thực dương thỏa mãn
log
2
x
+
log
2
y
+
1
≥
log
2
(
x
2
+
2
y
)
Tìm giá trị nhỏ nhất của P x + 2y A.
P
9
B.
P
2
2
+
3
C.
P
2
+...
Đọc tiếp
Cho x, y là số thực dương thỏa mãn log 2 x + log 2 y + 1 ≥ log 2 ( x 2 + 2 y ) Tìm giá trị nhỏ nhất của P = x + 2y
A. P = 9
B. P = 2 2 + 3
C. P = 2 + 3 2
D. P = 3 + 3
Cho hàm số f(x) log2x và g(x) log2(4-x) . Tìm tập nghiệm của bất phương trình f(x + 1) g(x + 2) A.
S
-
∞
;
1
2
B.
S
-
1
;
1
2
C. S (0; 2). D.
S...
Đọc tiếp
Cho hàm số f(x) = log2x và g(x) = log2(4-x) . Tìm tập nghiệm của bất phương trình f(x + 1) < g(x + 2)
A. S = - ∞ ; 1 2
B. S = - 1 ; 1 2
C. S = (0; 2).
D. S = - ∞ ; 2
Chọn B.
Ta có: f(x + 1) = log2(x + 1) và g(x + 2) = log2(2 - x)
Đúng 0
Bình luận (0)
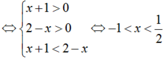
Tìm tập hợp nghiệm của phương trình log 2 + log 2 x - 1 = 1
A. {1} B. {2}
C. {1;2} D. {-1;2}
Giải phương trình log 2 ( x + 1 ) = l o g 2 ( x 2 + 2 ) - 1
A. x = 1
B. x = 0
C. x = 0, x = -4
D. x = 0, x = 1
Tổng các nghiệm của phương trình
1
+
log
2
x
+
1
3
log
2
-
x
3
+
3
x
2
+...
Đọc tiếp
Tổng các nghiệm của phương trình 1 + log 2 x + 1 3 = log 2 - x 3 + 3 x 2 + 3 x có dạng a + c b - b b a , b , c ∈ ℕ . Giá trị a + b + c là:
A. 9
B. 10
C. 11
D. 12
