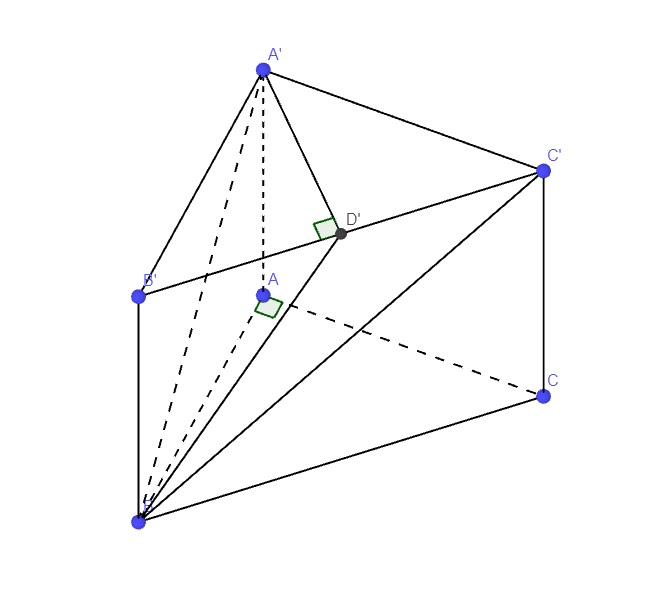
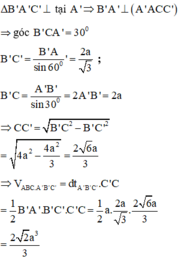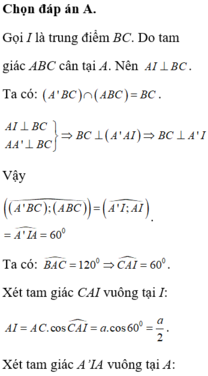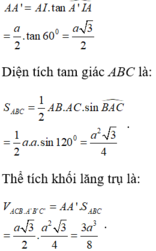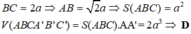cho lăng trụ đứng ABCA'B'C' có ABC là tam giác vuông cân tại A với AB=a, A'B' tạo với mặt phẳng <ABC> một góc 600 .Thể tích lăng trụ ABCA'B'C'

Những câu hỏi liên quan
Cho lăng trụ đứng ABCABC có đáy ABC là tam giác vuông tại A, ABa,
A
C
B
^
60
°
, BC tạo với mặt phẳng AACC một góc
30
°
. Thể tích của khối lăng trụ ABCABC bằng
Đọc tiếp
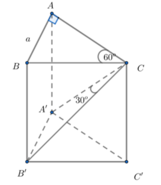
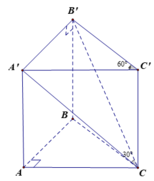
Cho lăng trụ đứng ABCA'B'C' có đáy ABC là tam giác vuông tại A, AB=a, A C B ^ = 60 ° , B'C tạo với mặt phẳng AA'CC' một góc 30 ° . Thể tích của khối lăng trụ ABCA'B'C' bằng
![]()
![]()
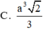
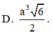
Cho lăng trụ đứng
A
B
C
A
B
C
có đáy ABC là tam giác vuông tại A,
A
B
a
,
A
C
B
60
°
,
B
C
tạo với mặt phẳng AACC một góc
30
°
. Tính thể tích V của khối lăng trụ
A...
Đọc tiếp
Cho lăng trụ đứng A B C A ' B ' C ' có đáy ABC là tam giác vuông tại A, A B = a , A C B = 60 ° , B ' C tạo với mặt phẳng AA'CC' một góc 30 ° . Tính thể tích V của khối lăng trụ A B C A ' B ' C ' .
A. V = a 3 2
B. V = a 3 3
C. V = a 3 2 3
D. V = a 3 6 2
Cho khối lăng trụ đứng ABCABC có đáy ABC là tam giác cân với ABACa, góc
B
A
C
^
120
°
. Mặt phẳng (ABC) tạo với đáy một góc bằng
60
°
. Thể tích của khối lăng trụ ABCABC là A.
3
a
3
8
B. ...
Đọc tiếp
Cho khối lăng trụ đứng ABCA'B'C' có đáy ABC là tam giác cân với AB=AC=a, góc B A C ^ = 120 ° . Mặt phẳng (A'BC) tạo với đáy một góc bằng 60 ° . Thể tích của khối lăng trụ ABCA'B'C' là
A. 3 a 3 8
B. 9 a 3 8
C. a 3 8
D. 3 a 3 4
Cho lăng trụ đứng
A
B
C
A
B
C
có đáy ABC là tam giác vuông tại A,
A
B
a
,
A
C
B
60
°
, BC tạo với mặt phẳng
A
A
C
C
một góc
30
°
. Thể tích của khối lăng trụ bằng A.
a
3...
Đọc tiếp
Cho lăng trụ đứng A B C A ' B ' C ' có đáy ABC là tam giác vuông tại A, A B = a , A C B = 60 ° , B'C tạo với mặt phẳng A A ' C C ' một góc 30 ° . Thể tích của khối lăng trụ bằng
A. a 3 2
B. a 3 3
C. a 3 2 3
D. a 3 6 2
Chọn C.
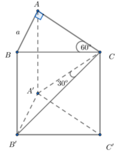
Phương pháp: Sử dụng định ly Pytago và lượng giác để tính các cạnh.

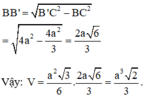
Đúng 0
Bình luận (0)
Lăng trụ đứng ABC.ABC có đáy ABC là tam giác vuông cân tại A; ABACa
5
; AB tạo với mặt đáy lăng trụ góc
60
0
. Thể tích khối lăng trụ bằng:
Đọc tiếp
Lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A; AB=AC=a 5 ; A'B tạo với mặt đáy lăng trụ góc 60 0 . Thể tích khối lăng trụ bằng:
![]()
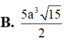
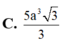
![]()
Lăng trụ đứng ABC.ABC có đáy ABC là tam giác vuông cân tại A, AB AC
a
5
, AB tạo với mặt đáy lăng trụ góc 600. Tính thể tích khối lăng trụ. A.
a
3
6
B.
5
a
3
15
2
C.
5
a...
Đọc tiếp
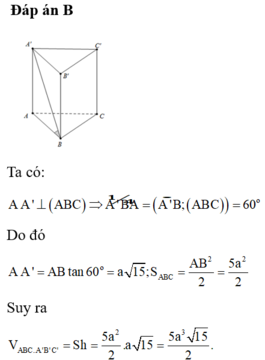
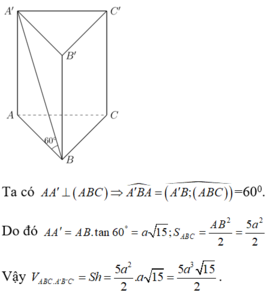
Lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, AB =AC = a 5 , A'B tạo với mặt đáy lăng trụ góc 600. Tính thể tích khối lăng trụ.
A. a 3 6
B. 5 a 3 15 2
C. 5 a 3 3 3
D. 4 a 3 6
Cho hình lăng trụ đứng ABCABC có đáy ABC là tam giác vuông cân tại A, mặt bên BCCB là hình vuông cạnh
2
α
. Thể tích của khối lăng trụ ABCABC bằng
Đọc tiếp
Cho hình lăng trụ đứng ABCA'B'C' có đáy ABC là tam giác vuông cân tại A, mặt bên BCC'B' là hình vuông cạnh 2 α . Thể tích của khối lăng trụ ABCA'B'C' bằng
![]()
![]()

![]()
giúp tớ.
cho lăng trụ ABCA'B'C' có đáy ABC là tam giác vuông cân tại B, AC=2a. hình chiếu vuông góc của A'B lên mặt phẳng (ABC) là trung điểm của AB. đường thẳng A'B tạo với mặt phẳng (ABC) một góc bằng 45 độ. chứng minh A'B vuông góc với B'C
Cho khối lăng trụ đứng ABC.ABC có đáy ABC là tam giác vuông cân tại A với ABa, AB tạo với mặt phẳng (ABC) một góc
α
. Biết thể tích lăng trụ ABC.ABClà
a
3
3
2
. Tính
α
. A.
α
70
∘
B.
α
30
∘
C. ...
Đọc tiếp
Cho khối lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A với AB=a, A'B tạo với mặt phẳng (ABC) một góc α . Biết thể tích lăng trụ ABC.A'B'C'là a 3 3 2 . Tính α .
A. α = 70 ∘
B. α = 30 ∘
C. α = 45 ∘
D. α = 60 ∘
Đáp án D

Ta có: S A B C = A B 2 2 = a 2 2 ⇒ A A ' = V S = a 3
Do A A ' ⊥ A B C ⇒ A ' B A ^ = α
⇒ tan α = A A ' A B = 3 ⇒ α = 60 ∘
Đúng 0
Bình luận (0)
Cho lăng trụ đứng ABCA'B'C' có đáy là tam giác vuông cân tại A với AB = AC = a, A'B tạo với đáy 1 góc α biết tanα = 2
a, Tính (A'B; (BCC'B'))
b, Tính (C'B; (A'B'BA))
\(A'A\perp\left(ABC\right)\) theo giả thiết \(\Rightarrow\widehat{A'BA}\) là góc giữa A'B và đáy
\(\Rightarrow tan\widehat{A'BA}=2\Rightarrow A'A=AB.tan\widehat{A'BA}=2a\)
a.
Gọi D' là trung điểm B'C' \(\Rightarrow A'D'\perp B'C'\) (đáy là tam giác vuông cân)
\(\Rightarrow A'D'\perp\left(BCC'B'\right)\Rightarrow\widehat{A'BD'}\) là góc giữa A'B và (BCC'B')
\(A'B=\sqrt{AB^2+A'A^2}=a\sqrt{5}\)
\(A'D'=\dfrac{1}{2}B'C'=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow sin\widehat{A'BD'}=\dfrac{A'D'}{A'B}=\dfrac{\sqrt{10}}{10}\Rightarrow\widehat{A'BD'}\approx18^026'\)
b.
\(\left\{{}\begin{matrix}A'C'\perp A'B'\left(gt\right)\\A'A\perp\left(A'B'C'\right)\Rightarrow A'A\perp A'C'\end{matrix}\right.\)
\(\Rightarrow A'C'\perp\left(ABB'A'\right)\Rightarrow\widehat{C'BA'}\) là góc giữa C'B và (ABB'A')
\(tan\widehat{C'BA'}=\dfrac{A'C'}{A'B}=\dfrac{a}{a\sqrt{5}}=\dfrac{1}{\sqrt{5}}\)
\(\Rightarrow\widehat{C'BA'}\approx24^06'\)
Đúng 3
Bình luận (0)