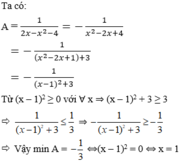tìm giá trị nhỏ nhất của biểu thức A= 3x2 - 12x+10

Những câu hỏi liên quan
Tìm giá trị lớn nhất của biểu thức:
C= -3x2+12x-7
\(C=-3x^2+12x-7=-3\left(x^2-4x+4\right)+12-7=-3\left(x-2\right)^2+5\le5\)
\(maxC=5\Leftrightarrow x=2\)
Đúng 1
Bình luận (0)
\(C=-3\left(x^2+4x+4\right)+5=-3\left(x+2\right)^2+5\le5\)
Dấu \("="\Leftrightarrow x=-2\)
Đúng 2
Bình luận (0)
a, Tìm giá trị lớn nhất của biểu thức: A=4x-x^2+3
b. Tìm giá trị nhỏ nhất của biểu thức:B=4x^2-12x+15
c,Tìm giá trị nhỏ nhất của biểu thức:C=4x^2+2y^2-4xy-4y+1
a)
\(A=4x-x^2+3=-\left(x^2-4x-3\right)=-\left(x^2-4x+4\right)+7=-\left(x-2\right)^2+7\le7\)
Daaus = xayr ra khi: x = 2
b) \(B=4x^2-12x+15=4\left(x^2-3x+9\right)-21=4\left(x-3\right)^2-21\ge-21\)
Dấu = xảy ra khi x = 3
c) \(C=4x^2+2y^2-4xy-4y+1=\left(4x^2-4xy+y^2\right)+\left(y^2-4y+4\right)-3=\left(2x-y\right)^2+\left(y-2\right)^2-3\ge-3\)
Dấu = xảy ra khi
2x = y và y = 2
=> x = 1 và y = 2
Đúng 1
Bình luận (0)
a) A = \(-x^2+4x+3=-\left(x-2\right)^2+7\le7\)
Dấu "=" <=> x = 2
b) \(4x^2-12x+15=\left(2x-3\right)^2+6\ge6\)
Dấu "=" xảy ra <=> \(x=\dfrac{3}{2}\)
c) \(4x^2+2y^2-4xy-4y+1\)
= \(\left(4x^2-4xy+y^2\right)+\left(y^2-4y+4\right)-3\)
= \(\left(2x-y\right)^2+\left(y-2\right)^2-3\ge-3\)
Dấu "=" <=> \(\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
tìm giá trị nhỏ nhất của biểu thức sau : A=\(4x^2-12x+10\)
ta có 4X2-12X+10= 4X2-2*2*3X+32+1=(2X-3)2+1
(2x-3)2>=0 => ( 2X-3)2+1>=1
Biểu thức đạt giá trị nhỏ nhất là 1
khi đó 2X-3=0 => X=3/2
Đúng 0
Bình luận (0)
Ta có: 4x^2 - 12x + 10 = 4x^2 - 6x - 6x +9 + 1= [2x(2x-3) - 3(2x-3)] + 1 = (2x-3)^2 + 1
để (2x-3)^2 + 1 bé nhất thì (2x-3)^2 bé nhất => (2x-3)^2= 0 => (2x-3)^2 + 1 = 1
Vậy giá trị bé nhất của A=.. là 1
Đúng 0
Bình luận (0)
4x^2-12x+10
=4x^2-12x+9+1
=(2x-3)^2+1
Ma: (2x-3)^2 >=1
=> (2x-3)^2+1>=1
Vay GTNN la 1
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm giá trị nhỏ nhất của biểu thức sau :
a) x²+12x+39
b) 9x²-12x
Xem chi tiết
\(a,x^2+12x+39=x^2+12x+36+3=\left(x+6\right)^2+3\ge3\forall x\)
Dấu = xảy ra \(\Leftrightarrow x+6=0\)
\(\Leftrightarrow x=-6\)
Vậy ...
\(b,9x^2-12x=9x^2-12x+4-4=\left(3x-2\right)^2-4\ge-4\forall x\)
Dấu = xảy ra \(\Leftrightarrow3x-2=0\)
\(\Leftrightarrow x=\frac{2}{3}\)
Vậy ...
Trả lời:
a, \(x^2+12x+39=x^2+2.x.6+36+3=\left(x+6\right)^2+3\ge3\forall x\)
Dấu "=" xảy ra khi x + 6 = 0 <=> x = - 6
Vậy GTNN của biểu thức bằng 3 khi x = - 6
b, \(9x^2-12x=\left(3x\right)^2-2.3x.2+4-4=\left(3x-2\right)^2-4\ge-4\forall x\)
Dấu "=" xảy ra khi 3x - 2 = 0 <=> x = 2/3
Vậy GTNN của biểu thức bằng - 4 khi x = 2/3
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
f
x
2
x
3
-
3
x
2
-
12
x
+
10
trên đoạn [-3;3] là A.
m
a
x
[
-
3
;
3
]
f...
Đọc tiếp
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x = 2 x 3 - 3 x 2 - 12 x + 10 trên đoạn [-3;3] là
A. m a x [ - 3 ; 3 ] f x = 1 ; m i n [ - 3 ; 3 ] f x = - 35
B. m a x [ - 3 ; 3 ] f x = 1 ; m i n [ - 3 ; 3 ] f x = - 10
C. m a x [ - 3 ; 3 ] f x = 17 ; m i n [ - 3 ; 3 ] f x = - 10
D. m a x [ - 3 ; 3 ] f x = 17 ; m i n [ - 3 ; 3 ] f x = - 35
Đáp án D
f x = 2 x 3 - 3 x 2 - 12 x + 10 ⇔ f ' x = 6 x 2 - 6 x - 12 ⇔ x = - 1 ; x = 2
So sánh f - 3 = - 35 , f - 1 = 17 , f 2 = - 10 , f 3 = 1
m a x [ - 3 ; 3 ] f x = 17 ; m i n [ - 3 ; 3 ] f x = - 35 .
Đúng 0
Bình luận (0)
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
f
x
2
x
3
-
3
x
2
-
12
x
+
10
trên đoạn
-
3
;
3
là A.
m
a
x
-...
Đọc tiếp
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x = 2 x 3 - 3 x 2 - 12 x + 10 trên đoạn - 3 ; 3 là
A. m a x - 3 ; 3 f x = 1 ; m i n - 3 ; 3 f x = - 35
B. m a x - 3 ; 3 f x = 17 ; m i n - 3 ; 3 f x = - 10
C. m a x - 3 ; 3 f x = 17 ; m i n - 3 ; 3 f x = - 35
D. m a x - 3 ; 3 f x = 1 ; m i n - 3 ; 3 f x = - 10
Chọn đáp án C.
Ta có hàm số liên tục trên đoạn [-3;3]
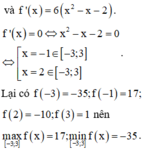
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức A = 1 2 x - x 2 - 4
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 x 3 - 3 x 2 - 12 x + 10 trên đoạn [-3;3] là
A. -18
B. -1
C. 7
D. 18
Chọn đáp án A
Phương pháp
- Tính y’ và tìm nghiệm của y’=0 trên đoạn [-3;3].
- Tính giá trị của hàm số tại hai điểm -3;3 và các điểm là nghiệm của đạo hàm ở trên.
- So sánh kết quả và kết luận.
Cách giải
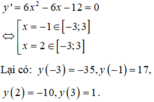
Do đó giá trị lớn nhất của hàm số trên [-3;3] là M=17 và giá trị nhỏ nhất của hàm số trên [-3;3] là m=-35
Vậy T=-18.
Đúng 0
Bình luận (0)
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 x 3 - 3 x 2 - 12 x + 10 trên đoạn - 3 ; 3 là:
A. -18
B. -1
C. 7
D. 18
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 x 3 - 3 x 2 - 12 x + 10 trên đoạn [ - 3 ; 3 ] là:
A. -1
B. 18
C. -18
D. 7