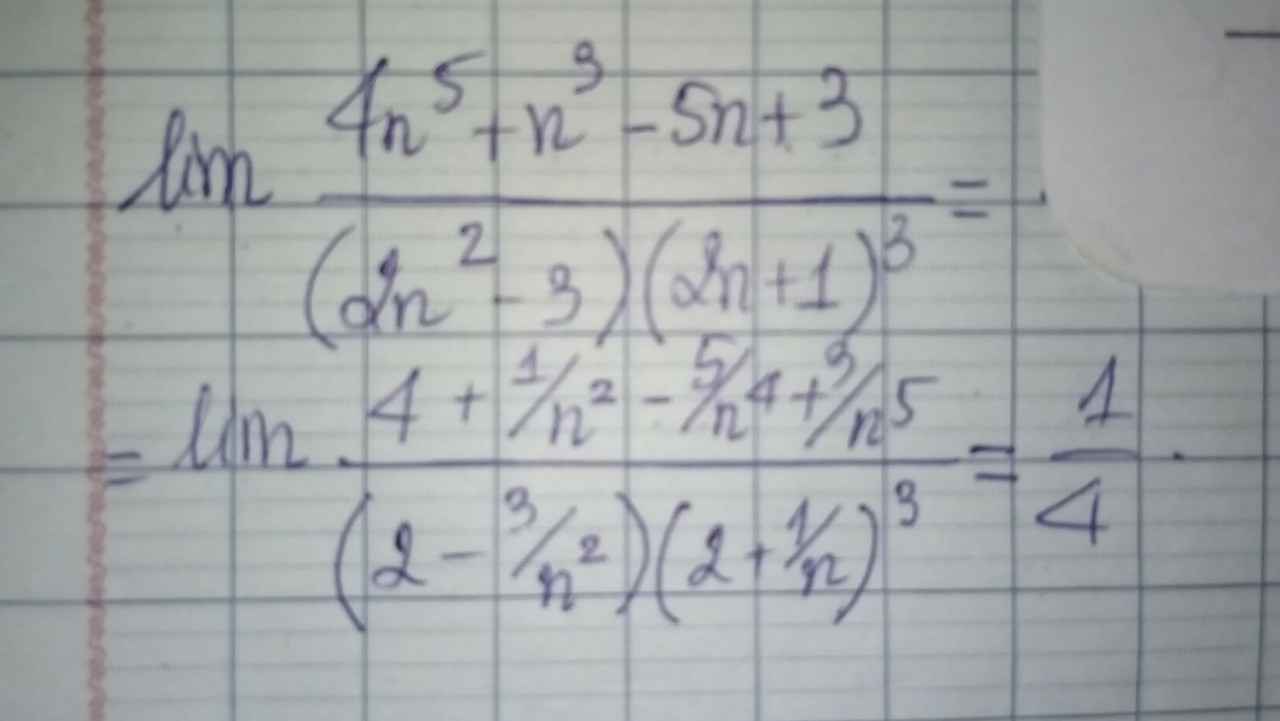\(2n+9⋮3n+1\)

\(\Rightarrow3\left(2n+9\right)⋮3n+1\)

\(\Rightarrow2\left(3n+1\right)+25⋮3n+1\)

\(\Rightarrow25⋮3n+1\)

\(\Rightarrow3n+1\in\left\{5,25,1,-5,-25,-1\right\}\)

\(n\in\left\{8,0\right\}\)

\(5n+2⋮9-2n\)

\(\Rightarrow2\left(5n+2\right)⋮9-2n\)

\(\Rightarrow-5\left(9-2n\right)-41⋮9-2n\)

\(41⋮9-2n\)

\(\Rightarrow9-2n\in\left\{41,-41,1,-1\right\}\)

\(\Rightarrow n\in\left\{-16,25,4,-5\right\}\)

\(\lim\left(\sqrt{4n^2+5n}-2n\right)=\lim\dfrac{5n}{\sqrt{4n^2+5n}+2n}=\lim\dfrac{5}{\sqrt{4+\dfrac{5}{n}}+2}=\dfrac{5}{\sqrt{4+0}+2}=\dfrac{5}{4}\)

\(\lim\left(\sqrt{2n+1}-\sqrt{n}\right)=\lim\sqrt{n}\left(\sqrt{2+\dfrac{1}{n}}-1\right)=+\infty.\left(\sqrt{2}-1\right)=+\infty\) (do \(\sqrt{2}-1>0\))

\(a,lim\left(\sqrt{4n^2+5n}-2n\right)\)

\(=limn\left(\sqrt{4+\dfrac{5}{n}}-2\right)=n.0=0\)

\(b,lim\left(\sqrt{2n+1}-\sqrt{n}\right)\)

\(=lim\sqrt{n}\left(\sqrt{2+\dfrac{1}{n}}-1\right)=\sqrt{n}\left(\sqrt{2}-1\right)=+\infty\)

Đây có đề bài bạn yêu cầu không, Hạnh?

Lời giải:
\(\lim \frac{4n^5+n^3-5n+3}{(2n^2-3)(2n+1)^3}=\lim \frac{4+\frac{1}{n^2}-\frac{5}{n^4}+\frac{3}{n^5}}{(2-\frac{3}{n^2})(2+\frac{1}{n})^3}=\frac{4}{2.2^3}=\frac{1}{4}\)

\(a=\lim\left(\dfrac{2n^3\left(5n+1\right)+\left(2n^2+3\right)\left(1-5n^2\right)}{\left(2n^2+3\right)\left(5n+1\right)}\right)\)

\(=\lim\left(\dfrac{2n^3-13n^2+3}{\left(2n^2+3\right)\left(5n+1\right)}\right)=\lim\dfrac{2-\dfrac{13}{n}+\dfrac{3}{n^3}}{\left(2+\dfrac{3}{n^2}\right)\left(5+\dfrac{1}{n}\right)}=\dfrac{2}{2.5}=\dfrac{1}{5}\)

\(b=\lim\left(\dfrac{n-2}{\sqrt{n^2+n}+\sqrt{n^2+2}}\right)=\lim\dfrac{1-\dfrac{2}{n}}{\sqrt{1+\dfrac{1}{n}}+\sqrt{1+\dfrac{2}{n}}}=\dfrac{1}{2}\)

\(c=\lim\dfrac{\sqrt{1+\dfrac{3}{n^3}-\dfrac{2}{n^4}}}{2-\dfrac{2}{n}+\dfrac{3}{n^2}}=\dfrac{1}{2}\)

\(d=\lim\dfrac{\sqrt{1-\dfrac{4}{n}}-\sqrt{4+\dfrac{1}{n^2}}}{\sqrt{3+\dfrac{1}{n^2}}-1}=\dfrac{1-2}{\sqrt{3}-1}=-\dfrac{1+\sqrt{3}}{2}\)

Lim 3.4n-2.13n/5n+6.13n

a/ \(=lim\frac{\left(-\frac{2}{3}\right)^n+1}{-2.\left(-\frac{2}{3}\right)^n+3}=\frac{1}{3}\)

b/ \(=lim\frac{\left(2-\frac{1}{n}\right)\left(1+\frac{1}{n}\right)\left(3+\frac{4}{n}\right)}{\left(\frac{5}{n}-6\right)^3}=\frac{2.1.3}{\left(-6\right)^3}=-\frac{1}{36}\)

c/ \(=lim\frac{5n+3}{\sqrt{n^2+5n+1}+\sqrt{n^2-2}}=\frac{5+\frac{3}{n}}{\sqrt{1+\frac{5}{n}+\frac{1}{n^2}}+\sqrt{1-\frac{2}{n}}}=\frac{5}{1+1}=\frac{5}{2}\)

d/ \(=lim\frac{5.\left(\frac{1}{2}\right)^n-6}{4.\left(\frac{1}{3}\right)^n+1}=\frac{-6}{1}=-6\)

e/ \(=-n^3\left(2+\frac{3}{n}-\frac{5}{n^2}+\frac{2020}{n^3}\right)=-\infty.2=-\infty\)

\(lim\left(5n-\sqrt{25n^2-3n+5}\right)=lim\dfrac{25n^2-25n^2+3n-5}{5n+\sqrt{25n^2-3n+5}}\)

\(=lim\dfrac{3n-5}{5n+\sqrt{25n^2-3n+5}}=lim\dfrac{3-\dfrac{5}{n}}{5+\sqrt{25-\dfrac{3}{n}+\dfrac{5}{n^2}}}=\dfrac{3-0}{5+\sqrt{25-0+0}}=\dfrac{3}{10}\)

\(lim\dfrac{4n^5-3n^4-2n^3+7n-9}{-5n\left(3n^2-3n+1\right)\left(5-2n^2\right)}=lim\dfrac{\dfrac{4n^5-3n^4-2n^3+7n-9}{n^5}}{\dfrac{-5n}{n}\dfrac{\left(3n^2-3n+1\right)}{n^2}\dfrac{\left(5-2n^2\right)}{n^2}}\)

\(=lim\dfrac{4-\dfrac{3}{n}-\dfrac{2}{n^2}+\dfrac{7}{n^4}-\dfrac{9}{n^5}}{-5.\left(3-\dfrac{2}{n}+\dfrac{1}{n^2}\right).\left(\dfrac{5}{n^2}-2\right)}=\dfrac{4-0-0+0-0}{-5\left(3-0+0\right).\left(0-2\right)}=\dfrac{2}{15}\)

Không hiểu câu hỏi lắm :vvv