\(\dfrac{4x+2}{4x-2}+\dfrac{3-6x}{6x-6}\left(dkxd:x\ne\dfrac{1}{2};x\ne1\right)\)

\(=\dfrac{2\left(2x+1\right)}{2\left(2x-1\right)}+\dfrac{3\left(1-2x\right)}{6\left(x-1\right)}\)

\(=\dfrac{2x+1}{2x-1}+\dfrac{1-2x}{2\left(x-1\right)}\)

\(=\dfrac{2x+1}{2x-1}+\dfrac{1-2x}{2x-2}\)

\(=\dfrac{\left(2x+1\right)\left(2x-2\right)}{\left(2x-1\right)\left(2x-2\right)}+\dfrac{\left(1-2x\right)\left(2x-1\right)}{\left(2x-1\right)\left(2x-2\right)}\)

\(=\dfrac{4x^2-2x-2}{\left(2x-1\right)\left(2x-2\right)}+\dfrac{-4x^2+4x-1}{\left(2x-1\right)\left(2x-2\right)}\)

\(=\dfrac{4x^2-2x-2-4x^2+4x-1}{\left(2x-1\right)\left(2x-2\right)}\)

\(=\dfrac{2x-3}{\left(2x-1\right)\left(2x-2\right)}\)

\(=\dfrac{2x-3}{4x^2-6x+2}\)

Bài 5 câu a ạ 

\(a,A=x^2-6x-2=\left(x-3\right)^2-11\ge-11\)

Dấu \("="\Leftrightarrow x=3\)

\(b,B=6x-9x^2+2=-\left(3x-1\right)^2+3\le3\)

Dấu \("="\Leftrightarrow x=\dfrac{1}{3}\)

A=\(x^2-6x-2<=> x^2-2.3x+9-11<=>(x-9)^2-11\)

\((x^2-9)> hoặc = 0 \rightarow (x^2-9)-11> hoặc = -11\)

A > hoặc = -11, dấu'=' xảy ra <=> A=-11

<=> x-9=0 <=> x=9

A_min= -11 <=> x=9

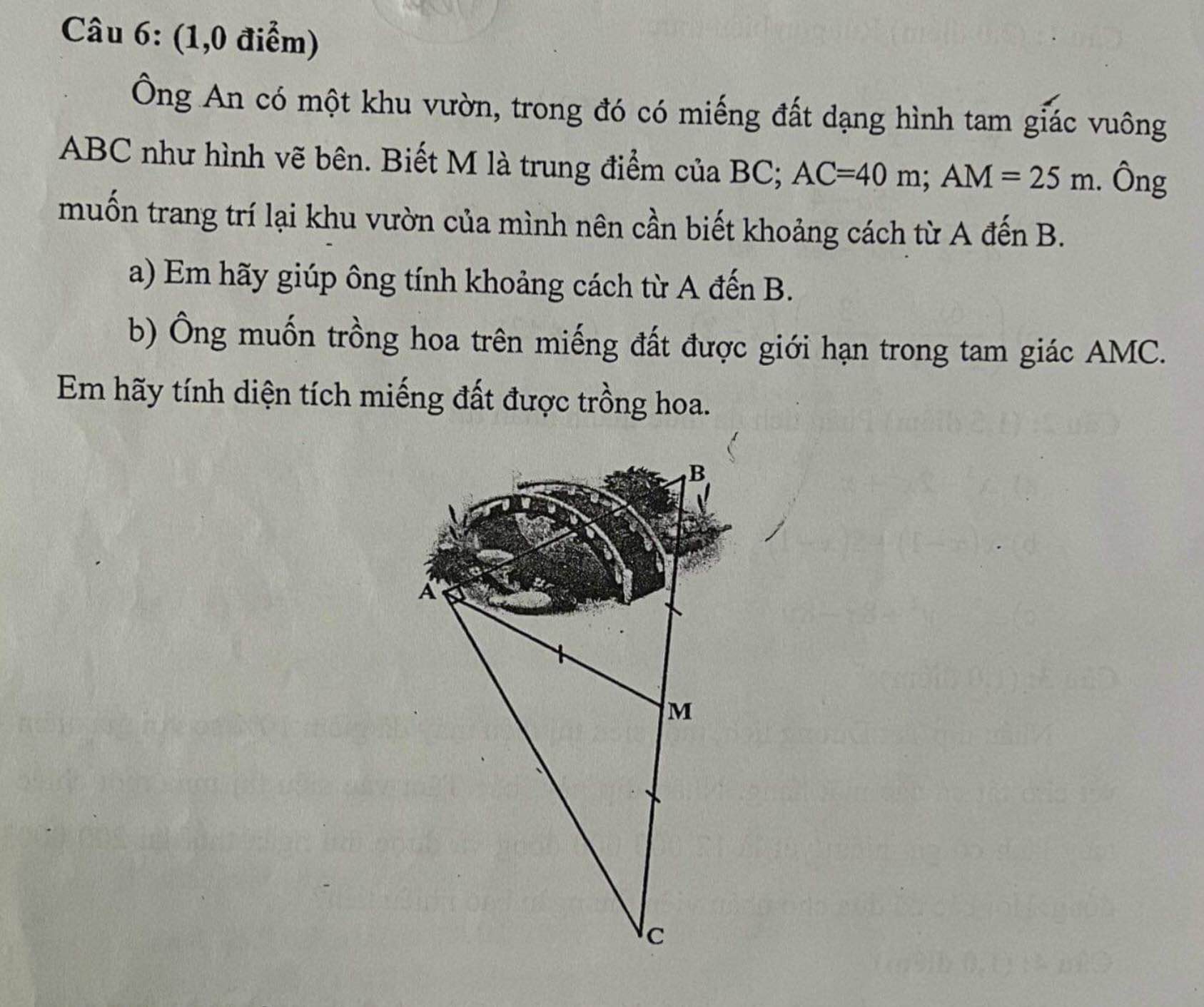
Tam giác ABC vuông tại A có AM là trung tuyến ứng với cạnh huyền

\(\Rightarrow AM=\dfrac{1}{2}BC\Rightarrow BC=2AM=50\left(m\right)\)

a. Áp dụng định lý Pitago:

\(AB=\sqrt{BC^2-AC^2}=30\left(m\right)\)

b. Kẻ \(MH\perp AC\Rightarrow MH||AB\) (cùng vuông góc AC)

Mà M là trung điểm BC \(\Rightarrow MH\) là đường trung bình tam giác ABC

\(\Rightarrow MH=\dfrac{1}{2}AB=15\left(m\right)\)

\(\Rightarrow S_{AMC}=\dfrac{1}{2}MH.AC=\dfrac{1}{2}.15.40=300\left(m^2\right)\)

em ơi chưa có bài em nhé, em chưa tải bài lên lám sao mình giúp được 

Dạ đề đây ạ   

Dạ đề đây ạ  

Câu 1: C

Câu 2: B

Câu 3: A

Câu 4: C

Câu 5: B

Câu 6: A

Câu 7: B

Câu 8: A

Câu 9: D

Câu 10: B

Câu 11: B

Câu 12: D

Câu 13: A

Câu 14: B

Câu 15: B

Câu 16: C

Câu 17: C 
Câu 18: \(\left\{{}\begin{matrix}a:D\\b:B\end{matrix}\right.\)

2. will visit/ am visiting

Tương lai đơn và tương lai gần (DHNB: tomorrow)

3. will have/ are having

Tương lai đơn và tương lai gần (DHNB: on the weekend)

4. produce 

Hiện tại đơn (DHNB: every year)

5. are wasting

Hiện tại tiếp diễn (DHNB: at the moment)

2 will visit (TLĐ: tomorrow)

3 will have (on the weekend: cuối tuần => TLĐ)

4 produce (HTĐ: every year)

5 are wasting (HTTD: at the moment)

Bài 4:

a) Vì $ABC$ cân tại $A$ nên $AB=AC$ và $\widehat{ABC}=\widehat{ACB}$

$\Rightarrow 180^0-\widehat{ABC}=180^0-\widehat{ACB}$

hay $\widehat{ABQ}=\widehat{ACR}$

Xét tam giác $ABQ$ và $ACR$ có:

$AB=AC$ (cmt)

$\widehat{ABQ}=\widehat{ACR}$ (cmt)

$BQ=CR$ (gt)

$\Rightarrow \triangle ABQ=\triangle ACR$ (c.g.c)

$\Rightarrow AQ=AR$

b) 

$H$ là trung điểm của $BC$ nên $HB=HC$

Mà $QB=CR nên $HB+QB=HC+CR$ hay $QH=HR$

Xét tam giác $AQH$ và $ARH$ có:

$AQ=AR$ (cmt)

$QH=RH$ (cmt)

$AH$ chung

$\Rightarrow \triangle AQH=\triangle ARH$ (c.c.c)

$\Rightarrow \widehat{QAH}=\widehat{RAH}$

Hình bài 4:

Bài 5:a) 

Xét tam giác vuông $AHB$ và $AHC$ có:

$AB=AC$ (do $ABC$ là tam giác cân ở A)

$\widehat{ABH}=\widehat{ACH}$ (do tam giác $ABC$ cân ở A)

$\Rightarrow \triangle AHB=\triangle AHC$ (cạnh huyền- góc nhọn)

$\Rightarrow HB=HC$ và $\widehat{BAH}=\widehat{CAH}$ (đpcm)

b) 

$HB=HC$ nên $H$ là trung điểm $BC$. Do đó $HB=BC:2=4$ (cm)

Áp dụng định lý Pitago:

$AH=\sqrt{AB^2-AH^2}=\sqrt{5^2-4^2}=3$ (cm)

c) 

Xét tam giác vuông $ADH$ và $AEH$ có:

$AH$ chung

$\widehat{DAH}=\widehat{EAH}$ (do $\widehat{BAH}=\widehat{CAH}$)

$\Rightarrow \triangle ADH=\triangle AEH$ (cạnh huyền- góc nhọn)

$\Rightarrow DH=EH$ nên tam giác $HDE$ cân tại $H$.