Lập bảng biến thiên và vẽ đồ thị hàm số : y = |-3x| - 3x
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6

Những câu hỏi liên quan
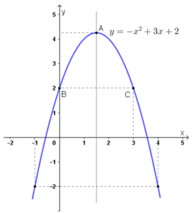
Lập bảng biến thiên và vẽ đồ thị của các hàm số: y = -x2 + 3x + 2
y = –x2 + 3x + 2 có a = –1 < 0, b = 3, c = 2:
+ Tập xác định D = R
+ Đồng biến trên 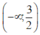 , nghịch biến trên
, nghịch biến trên 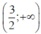
Bảng biến thiên:
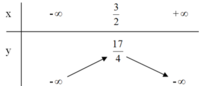
+ Đồ thị là parabol có:
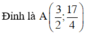
Trục đối xứng là đường thẳng x = 3/2
Giao điểm với trục tung là B(0 ; 2). Điểm đối xứng với B qua đường thẳng x = 3/2 là C(3 ; 2).
Đi qua các điểm (–1 ; –2) và (4 ; –2)
Đúng 0
Bình luận (0)
Lập bảng biến thiên và vẽ đồ thị của mỗi hàm số
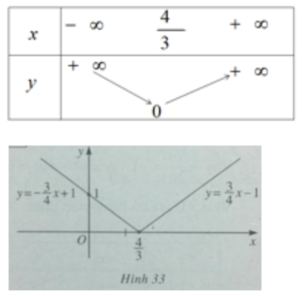
y = | - 3 x / 4 + 1 |
Bảng biến thiên và đồ thị của hàm số y = |-3x / 4 + 1| (h.33)
Đúng 0
Bình luận (0)
Cho hàm số y=f(x)= -3x^2+10x-4 a) Lập bảng biến thiên và vẽ đồ thị hàm số y= f(×) b) Từ bảng biến thiên, xác định khoảng đồng biến và nghịch biến và giá trị nhỏ nhất của hàm số trên c) Từ bảng biến thiên tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn [-1;2]
a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-10}{2\cdot\left(-3\right)}=\dfrac{10}{6}=\dfrac{5}{3}\\y=-\dfrac{10^2-4\cdot\left(-3\right)\cdot\left(-4\right)}{4\cdot\left(-3\right)}=\dfrac{13}{3}\end{matrix}\right.\)
Bảng biến thiên:
| x | -\(\infty\) 5/3 +\(\infty\) |
| y | +\(\infty\) 13/3 -\(\infty\) |

b: Hàm số đồng biến khi x<5/3; nghịch biến khi x>5/3
Giá trị nhỏ nhất là y=13/3 khi x=5/3
Đúng 2
Bình luận (0)
a. Tìm tập xác định của hàm số y = \(\frac{x+1}{2x+7}\)
b. Lập bảng biến thiên và vẽ đồ thị hàm số y = x2 + 3x + 2.
Lập bảng biến thiên và vẽ đồ thị của các hàm số :
a. \(y=x^2-2x-1\)
b. \(y=-x^2+3x+2\)
a) Tập xác định D = R
Bảng biến thiên
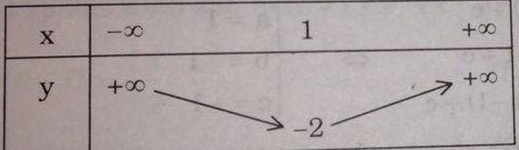
Đồ thị hàm số
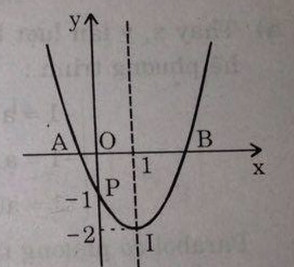
Đồ thị: parabol có đỉnh I(1, -2) với trục đối xứng x = 1
Giao điểm với trục tung là P(0,-1)
Giao điểm với trục hoành A (1-√2, 0) và B((1+√2, 0)
b)
Tập xác định D = R
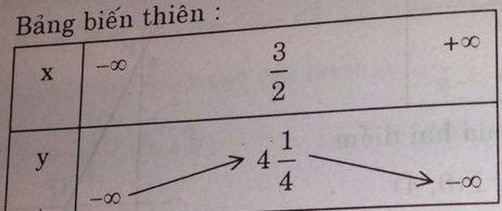
Đồ thị hàm số
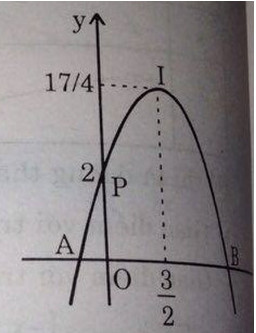
Đồ thị: parabol có đỉnh I \(\left(\dfrac{3}{2},\dfrac{17}{4}\right)\)với trục đối xứng \(x=\dfrac{3}{2}\)
Giao điểm với trục tung là P(0,2)
Giao điểm với trục hoành A \(\left(\dfrac{3-\sqrt{17}}{2},0\right)\) và B\(\left(\dfrac{3+\sqrt{17}}{2},0\right)\)
Đúng 0
Bình luận (0)
Lập bảng biến thiên và vẽ đồ thị của các hàm số :
a) \(y=-3x+2\)
b) \(y=2x^2\)
c) \(y=2x^2-3x+1\)
Lập bảng biến thiên và vẽ đồ thị của mỗi hàm số
y = x + | x |
Ta có thể viết
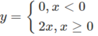
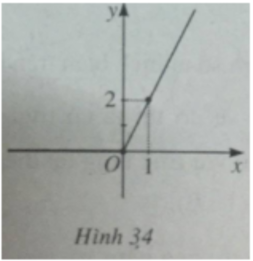
và đồ thị của hàm số y = x + |x| được vẽ trên hình 34.
Đúng 0
Bình luận (0)
Lập bảng biến thiên và vẽ đồ thị của mỗi hàm số
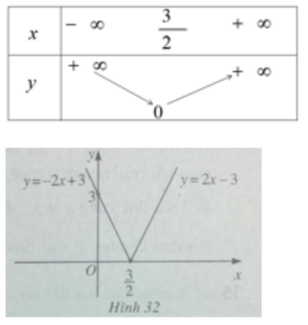
y = | 2 x - 3 |
Ta có thể viết

Từ đó có bảng biến thiên và đồ thị của hàm số
y = |2x - 3| (h.32)
Đúng 0
Bình luận (0)
Lập bảng biến thiên và vẽ đồ thị hàm số y = x 2 - 2 | x | + 1
Tập xác định của hàm số là D = R. Ngoài ra
f ( - x ) = ( - x ) 2 - 2 | - x | + 1 = x 2 - 2 x + 1
Hàm số là hàm số chẵn. Đồ thị của nó nhận trục tung làm trục đối xứng. Để xét chiều biến thiên và vẽ đồ thị của nó chỉ cần xét chiều biến thiên và vẽ đồ thị của nó trên nửa khoảng [ 0 ; + ∞ ) , rồi lấy đối xứng qua Oy. Với x ≥ 0 có f ( x ) = x 2 - 2 x + 1
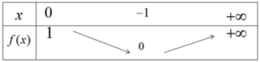
Bảng biến thiên
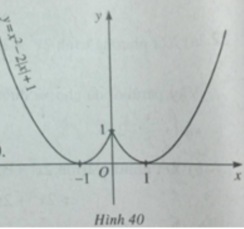
Đồ thị của hàm số đã cho được vẽ ở hình 40.
Đúng 1
Bình luận (0)
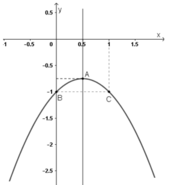
Lập bảng biến thiên và vẽ đồ thị của các hàm số: y = -x2 + x - 1
y = –x2 + x – 1
+ Tập xác định R
+ Đỉnh A(1/2 ; –3/4).
+ Trục đối xứng x = 1/2.
+ Đồ thị không giao với trục hoành.
+ Giao điểm với trục tung: B(0; –1).
Điểm đối xứng với B(0 ; –1) qua đường thẳng x = 1/2 là C(1 ; –1).
+ Bảng biến thiên:
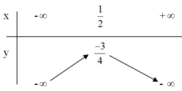
+ Đồ thị hàm số :
Đúng 0
Bình luận (0)










