STN a nhỏ nhất sao cho khi a : \(\dfrac{3}{5}\) và a : \(1\dfrac{3}{7}\) đều được kết quả là 1 STN

Những câu hỏi liên quan
STN a nhỏ nhất sao cho khi a chia cho 3/5 và\(1\frac{3}{7}\)ta đều đc kết quả là STN
Bài 1: Tìm số tự nhiên a nhỏ nhất sao cho khi chia a cho \(\dfrac{3}{5}\) và 1\(\dfrac{3}{7}\) ta đều được kết quả là các số tự nhiên.
Theo đề ta có: \(a:\dfrac{3}{5}\in N;a:\dfrac{10}{7}\in N\)
\(\Rightarrow a.\dfrac{5}{3}\in N;a.\dfrac{7}{10}\in N\)
Để \(a.\dfrac{5}{3}\in N\) và \(a.\dfrac{7}{10}\in N\)
thì \(a.5⋮3;a.7⋮10\)
mà 5 \(⋮̸\) 3;7 \(⋮̸\) 10
Nên a \(⋮\) 3 và a \(⋮\) 10 mà a nhỏ nhất
\(\Rightarrow a=BCNN\left(3,10\right)=30\)
Vậy a = 30.
Đúng 0
Bình luận (0)
\(1\dfrac{3}{7}=\dfrac{10}{7}\)
Ta có : \(\dfrac{a.5}{3}\)=N ; \(\dfrac{a.7}{10}\)=N và a nhỏ nhất
Suy ra :a(1)=3 ; a(2)=10
Vì a chia hết cho 10/7 và 3/5 suy ra a thuộc BCNN(3,10)
Suy ra : BCNN(3,10)=3.10=30
Suy ra :a = 30
Đúng 0
Bình luận (3)
tìm stn a nhỏ nhất sao cho khi chia a cho 8/9 và 12/17 thì kết quả đều được số tự nhiên
Tìm p/s dương a/b nhỏ nhất , khác 0 sao cho khi nhân p/s với số 24/5 và 16/3 đều được kquả là STN
ta có : ( gọi số cần tìm là \(\frac{a}{b}\))
*> \(\frac{a}{b}.\frac{24}{5}=\frac{24a}{5b}\)
do \(\frac{24a}{5b}\)là 1 số tự nhiên
=> 24 chia hết cho b , a chia hết cho 5 ( do chúng đôi một nguyên tố cùng nhau ) (1)
*> \(\frac{a}{b}.\frac{16}{3}=\frac{16a}{3b}\)
lập luận tương tự , ta có 16 chia hết cho b , a chia hết cho 3 (2)
Từ (1) và (2) , và do \(\frac{a}{b}\)nhỏ nhất <=> a nhỏ nhất , b lớn nhất
=> b thuộc ƯCLN ( 16 ; 24 ) ; a thuộc BCNN ( 3 ; 5 )
sau đó bạn tự tìm a và b nhé !! >-^
Đúng 0
Bình luận (0)
a,Chứng tỏ rằng A( 3+32+33+...+32000)chia hết cho 12b, tìm STN a nhỏ nhất sao cho khi chia a cho lần lượt các số 3, 5, 7 thì được số dư lần lượt là 2, 3, 4c, tìm P/s nhỏ nhất khác 0 saocho khi chia nó cho frac{35}{52}; frac{14}{39}đều được thương là 1 STN
Đọc tiếp
a,Chứng tỏ rằng A=( 3+32+33+...+32000)chia hết cho 12
b, tìm STN a nhỏ nhất sao cho khi chia a cho lần lượt các số 3, 5, 7 thì được số dư lần lượt là 2, 3, 4
c, tìm P/s nhỏ nhất khác 0 saocho khi chia nó cho \(\frac{35}{52}\); \(\frac{14}{39}\)
đều được thương là 1 STN
Câu hỏi của Kz9 - Toán lớp 6 - Học toán với OnlineMath
Em tham khảo câu b ở link này nhé
Đúng 0
Bình luận (0)
Tìm số tự nhiên a nhỏ nhất sao cho khi chia a cho \(\dfrac{6}{7}\) và chia a cho \(\dfrac{10}{11}\) ta đều được kết quả là số tự nhiên ?
Theo đề bài 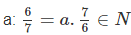
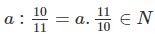
Để a nhỏ nhất thì a = BCNN(6;10) = 30
Vậy số phải tìm là 30
Đúng 0
Bình luận (0)
VTC nhập 1 số thực a từ bàn phím và tìm 1 stn n nhỏ nhất sao cho \(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{n}>a\)
ar s,a:real;
begin
readln(a);
s:=1;
n:=1;
while s <= a do
begin
n:=n+1;
s:=s+1/n;
end;
writeln('So n nho nhat de ',s,' < ',a,' la:',n);
readln;
end.
Đúng 0
Bình luận (0)
Tìm số tự nhiên a nhỏ nhất sao cho khi chia a cho 3/5 và chia a cho 1 3/7 ta đều được kết quả là một số tự nhiên. Số tự nhiên a là ...
tìm ps dương nhỏ nhất mà khi chia ps này cho các ps 7/12 và 8/21 thì được kết quả là 1 STN
gọi phân số cần tìm là a/b
ta có =) a/b chia hết cho 7/12
a/b chia hêt cho 8/21
=) a chia hết cho 7 ; 8
=) 12; 21 chia hết cho b
để a/b nhỏ nhất thì a phải nhỏ nhất , b phải lớn nhất
hay a là BCNN( 7;8)=) a = 56
hay b là UCLN(21;12 =) b = 3
vây phân so can tim la 56 / 3
Đúng 0
Bình luận (0)


















