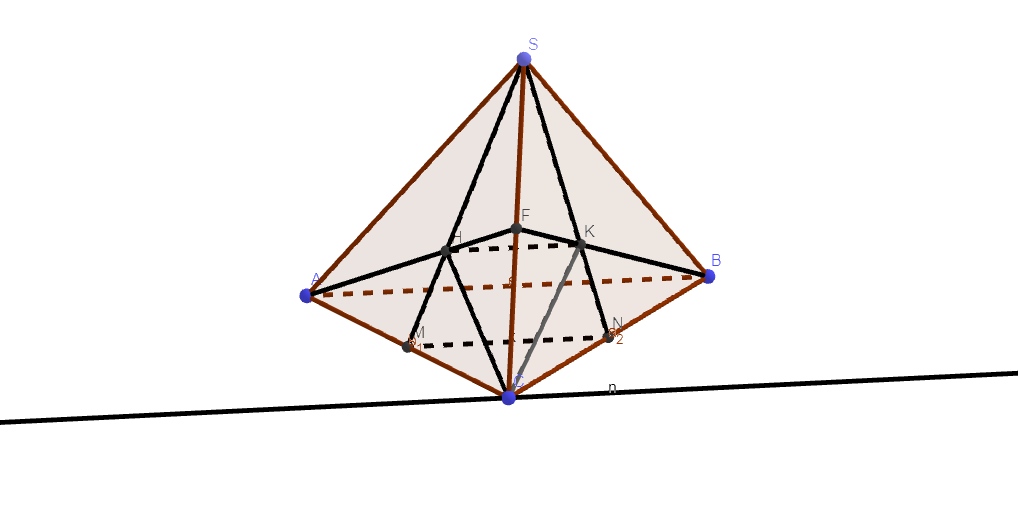
làm giúp em câu b theo phương pháp kẻ đường thẳng song song tại giao điểm của 2 mặt phẳng
Những câu hỏi liên quan
Số phát biểu đúng 1. Trong không gian qua 1 điểm không nằm trên đường thẳng cho trước, có một và chỉ một đường thẳng song song với đường thẳng đã cho 2. Nếu 3 mặt phẳng đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến ấy đồng quy 3. Nếu 2 mặt phẳng phân biệt lần lượt chứa 2 đường thẳng song song thì giao tuyến của chúng ( nếu có ) cũng song song với 2 đường thẳng đó hoặc trùng với một trong 2 đường thẳng đó 4. 2 đường thẳng phân biệt cùng song song với đường thẳng th...
Đọc tiếp
Số phát biểu đúng
1. Trong không gian qua 1 điểm không nằm trên đường thẳng cho trước, có một và chỉ một đường thẳng song song với đường thẳng đã cho
2. Nếu 3 mặt phẳng đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến ấy đồng quy
3. Nếu 2 mặt phẳng phân biệt lần lượt chứa 2 đường thẳng song song thì giao tuyến của chúng ( nếu có ) cũng song song với 2 đường thẳng đó hoặc trùng với một trong 2 đường thẳng đó
4. 2 đường thẳng phân biệt cùng song song với đường thẳng thứ 3 thì chúng song song với nhau
5. Nếu đường thẳng d không nằm trong mặt phẳng ( ) và d song song với đường thẳng d’ nằm trong ( ) thì d song song với ( )
6. Cho đường thẳng a song song với mặt phẳng . Nếu mặt phẳng chứa a và cắt theo giao tuyến b thì b song song với a
7. Nếu 2 mặt phẳng cùng song song với 1 đường thẳng thì giao tuyến của chúng ( nếu có ) cũng song song với đường thẳng đó
8. Cho 2 đường thẳng chéo nhau. Có vô số mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
A. 8
B. 7
C. 6
D. 5
Đáp án C
2. Nếu 3 mặt phẳng đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến ấy hoặc đồng quy, hoặc đôi một song song với nhau
8. Cho 2 đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia
Đúng 0
Bình luận (0)
Trong không gian, cho các mệnh đề sau:I. Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.II. Hai mặt phẳng phân biệt chứa hai đường thẳng song song cắt nhau theo giao tuyến song song với hai đường thẳng đó.III. Nếu đường thẳng a song song với đường thẳng b, đường thẳng b nằm trên mặt phẳng (P) thì a song song với (P).IV. Qua điểm A không thuộc mặt phẳng
(
α
)
, kẻ được đúng một đường thẳng song song với . Số mệnh đề đúng là A....
Đọc tiếp
Trong không gian, cho các mệnh đề sau:
I. Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.
II. Hai mặt phẳng phân biệt chứa hai đường thẳng song song cắt nhau theo giao tuyến song song với hai đường thẳng đó.
III. Nếu đường thẳng a song song với đường thẳng b, đường thẳng b nằm trên mặt phẳng (P) thì a song song với (P).
IV. Qua điểm A không thuộc mặt phẳng ( α ) , kẻ được đúng một đường thẳng song song với .
Số mệnh đề đúng là
A. 2
B. 0
C. 1
D. 3
Cho tam giác ABC. Từ A, kẻ đường thẳng song song với BC. Từ C, kẻ đường thẳng song song với AB. Hai đường thẳng này cắt nhau tại D.a, Cm ADBC và ABCDb, Gọi O là giao của AC và BD. Cm O là trung điểm của AC và BD.c, Qua O, kẻ đg thẳng bất kì cắt 2 đg thẳng AB và CD lần lượt ở M và N. Cm O là trung điểm của MN.Giúp mk mọi người ơi!!! Câu a mk làm đc rồi nha!!! Làm câu b và c giúp mk!!! Mk cảm ơn!!!
Đọc tiếp
Cho tam giác ABC. Từ A, kẻ đường thẳng song song với BC. Từ C, kẻ đường thẳng song song với AB. Hai đường thẳng này cắt nhau tại D.
a, Cm AD=BC và AB=CD
b, Gọi O là giao của AC và BD. Cm O là trung điểm của AC và BD.
c, Qua O, kẻ đg thẳng bất kì cắt 2 đg thẳng AB và CD lần lượt ở M và N. Cm O là trung điểm của MN.
Giúp mk mọi người ơi!!! Câu a mk làm đc rồi nha!!! Làm câu b và c giúp mk!!! Mk cảm ơn!!!
GIÚP MÌNH với !!!!!a) trong mặt phẳng tọa độ cho đường thẳng (d):y-x+2 lập phương trình đường thẳng (d) biết (d) đi qua điểm A(-2;1) và song song với đường thẳng (d).b)Gọi B là giao của (d) với trục tung và C là giao của (d) với trục hoành. Tính độ dài các cạnh của tam giác ABC.CÂU a) MÌNH LÀM ĐƯỢC RỒI; CHỈ CẦN NÊU ĐÁP ÁN KHÔNG PHẢI TRÌNH BÀY CÁCH LÀM. CÒN CÂU b) THÌ TRÌNH BÀY HẲN RA NHÉ!!!! THANKS :))))
Đọc tiếp
GIÚP MÌNH với !!!!!
a) trong mặt phẳng tọa độ cho đường thẳng (d):y=-x+2 lập phương trình đường thẳng (d') biết (d') đi qua điểm A(-2;1) và song song với đường thẳng (d).
b)Gọi B là giao của (d') với trục tung và C là giao của (d) với trục hoành. Tính độ dài các cạnh của tam giác ABC.
CÂU a) MÌNH LÀM ĐƯỢC RỒI; CHỈ CẦN NÊU ĐÁP ÁN KHÔNG PHẢI TRÌNH BÀY CÁCH LÀM. CÒN CÂU b) THÌ TRÌNH BÀY HẲN RA NHÉ!!!! THANKS :))))
a) (d') y =-x +b
=> 1 = -(-2) +b => b =-2
(d') y =-x -2
b) x =0 (d') => y = -2 B(0;-2)
y =0 (d) => -x+2 =0 => x = 2 => C(-2;0)
\(AB=\sqrt{\left(-2-0\right)^2+\left(1+2\right)^2}=2\sqrt{2}\)
\(AC=\sqrt{\left(-2+2\right)^2+\left(1-0\right)^2}=1\)
\(BC=\sqrt{\left(0+2\right)^2+\left(-2-0\right)^2}=2\sqrt{2}\)
Đúng 0
Bình luận (0)
Câu 1:Cho hình chóp S. ABCD có AB và CD không song song. Gọi M là một điểm thuộc miền trong của tam giác SCDa) Tìm giao điểm N của đường thẳng CD và mặt phẳng (SBM)b) Tìm giao tuyến của hai mặt phẳng (SBM) và (SAC)c) Tìm giao điểm I của đường thẳng BM và mặt phẳng (SAC)d) Tìm giao điểm P của SC và mặt pẳng (ABM), từ đó suy ra giao tuyến của hai mặt phẳng (SCD) và (ABM)Câu 2:Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Trong mặt phẳng đáy vẽ đường thẳng d đi qua A và không song song với cá...
Đọc tiếp
Câu 1:Cho hình chóp S. ABCD có AB và CD không song song. Gọi M là một điểm thuộc miền trong của tam giác SCD
a) Tìm giao điểm N của đường thẳng CD và mặt phẳng (SBM)
b) Tìm giao tuyến của hai mặt phẳng (SBM) và (SAC)
c) Tìm giao điểm I của đường thẳng BM và mặt phẳng (SAC)
d) Tìm giao điểm P của SC và mặt pẳng (ABM), từ đó suy ra giao tuyến của hai mặt phẳng (SCD) và (ABM)
Câu 2:
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Trong mặt phẳng đáy vẽ đường thẳng d đi qua A và không song song với các cạnh của hình bình hành, d cắt đoạn BC tại E. Gọi C' là một điểm nằm trên cạnh SC
a) Tìm giao điểm M của CD và mặt phẳng (C'AE)
b) Tìm thiết diện của hình chóp cắt bởi mặt phẳng (C'AE)
Cho tứ diện ABCD và điểm M nằm trong tam giác BCD.a) Dựng đường thẳng qua M song song với hai mặt phẳng (ABC) và (ABD). Giả sử đường thẳng này cắt mặt phẳng (ACD) tại B.Chứng minh rằng AB, BM và CD đồng quy tại một điểm.b) Chứng minh
M
B
B
A
d
t
∆
M...
Đọc tiếp
Cho tứ diện ABCD và điểm M nằm trong tam giác BCD.
a) Dựng đường thẳng qua M song song với hai mặt phẳng (ABC) và (ABD). Giả sử đường thẳng này cắt mặt phẳng (ACD) tại B'.
Chứng minh rằng AB', BM và CD đồng quy tại một điểm.
b) Chứng minh M B ' B A = d t ∆ M C D d t ∆ B C D
c) Đường thẳng song song với hai mặt phẳng (ACB) và (ACD) kẻ từ M cắt (ABD) tại C' và đường thẳng song song với hai mặt phẳng (ADC) và (ADB) kẻ từ M cắt (ABC) tại D'. Chứng minh rằng M B ' B A + M C ' C A + M D ' D A = 1
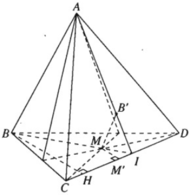
a) MB' qua M và song song với (ABC) và (ABD) ⇒ MB′ song song với giao tuyến AB của hai mặt phẳng này. Ta có: MB′ // AB nên MB' và AB xác định một mặt phẳng. Giả sử MB cắt AB' tại I.
Ta có: I ∈ BM ⇒ I ∈ (BCD)
I ∈ AB′ ⇒ I ∈ (ACD)
Nên I ∈ (BCD) ∩ (ACD) = CD
Có: I ∈ CD
Vậy ba đường thẳng AB', BM và CD đồng quy tại I.
b) MB′ // AB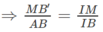 
Kẻ MM′ ⊥ CD và BH ⊥ CD
Ta có: MM′ // BH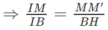 
Mặt khác:
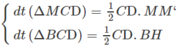
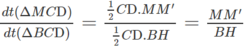
Do đó: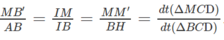 
Vậy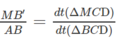 
c) Tương tự ta có: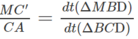 
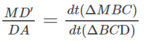
Vậy:
Đúng 0
Bình luận (0)
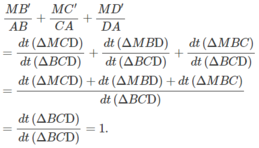
Nêu phương pháp chứng minh :
- Đường thẳng song song với đường thẳng
- Đường thẳng song song với mặt phẳng
- Mặt phẳng song song với mặt phẳng
Muốn chứng minh đường thẳng a // (P), ta chứng minh đường thẳng a song song với đường thẳng b mà đường thẳng b song song với mặt phẳng (P) (a và (P) không có điểm chung)
Đúng 0
Bình luận (0)
Giải mục 1 trang 101, 102 SGK Toán 11 tập 1 - Cánh Diều
14 tháng 7 2023 lúc 16:25
Cho đường thẳng a song song với mặt phẳng (P). Cho mặt phẳng (Q) chứa a và cắt (P) theo giao tuyển b. (Hình 51)
a) Giả sử a cắt b tại M. Đường thẳng a có cắt mặt phẳng (P) tại M hay không?
b) Nêu vị trí tương đối của hai đường thẳng a và b. Vì sao?
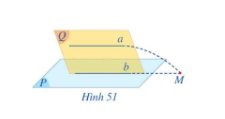
a) Ta có a ∩ b = {M} nên M ∈ b
Mà b ⊂ (P), do đó M ∈ (P).
Lại có M ∈ a.
Vậy đường thẳng a cắt mặt phẳng (P) tại M.
b) Theo câu a, nếu a cắt b tại M thì a cắt (P) tại M, điều này mâu thuẫn với giả thiết đường thẳng a song song với mặt phẳng (P).
Do đó a và b không cắt nhau và cùng nằm trong mặt phẳng (Q).
Suy ra a // b.
Vậy hai đường thẳng a và b song song với nhau.
Đúng 0
Bình luận (0)
Câu 1:Cho hình chóp S. ABCD có AB và CD không song song. Gọi M là một điểm thuộc miền trong của tam giác SCDa) Tìm giao điểm N của đường thẳng CD và mặt phẳng (SBM)b) Tìm giao tuyến của hai mặt phẳng (SBM) và (SAC)c) Tìm giao điểm I của đường thẳng BM và mặt phẳng (SAC)d) Tìm giao điểm P của SC và mặt pẳng (ABM), từ đó suy ra giao tuyến của hai mặt phẳng (SCD) và (ABM)Câu 2:Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Trong mặt phẳng đáy vẽ đường thẳng d đi qua A và không song song với cá...
Đọc tiếp
Câu 1:Cho hình chóp S. ABCD có AB và CD không song song. Gọi M là một điểm thuộc miền trong của tam giác SCD
a) Tìm giao điểm N của đường thẳng CD và mặt phẳng (SBM)
b) Tìm giao tuyến của hai mặt phẳng (SBM) và (SAC)
c) Tìm giao điểm I của đường thẳng BM và mặt phẳng (SAC)
d) Tìm giao điểm P của SC và mặt pẳng (ABM), từ đó suy ra giao tuyến của hai mặt phẳng (SCD) và (ABM)
Câu 2:
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Trong mặt phẳng đáy vẽ đường thẳng d đi qua A và không song song với các cạnh của hình bình hành, d cắt đoạn BC tại E. Gọi C' là một điểm nằm trên cạnh SC
a) Tìm giao điểm M của CD và mặt phẳng (C'AE)
b) Tìm thiết diện của hình chóp cắt bởi mặt phẳng (C'AE)
Câu 3:
Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của các cạnh AB và CD trên cạnh AD lấy điểm P không trùng với trung điểm của AD
a) Gọi E là giao điểm của đường thẳng MP và đường thẳng BD. Tìm giao tuyến của hai mặt phẳng (PMN) và (BCD)
b) Tìm giao điểm của mặt phẳng (PMN) và BC
Câu 4:
Cho bốn điểm A, B, C và D không đồng phẳng. Gọi I,K lần lượt là trung điểm của hai đoạn thẳng AD và BC
a) Tìm giao tuyến của hai mặt phẳng (IBC) và (KAD)
b) Gọi M và N là hai điểm lần lượt lấy trên hai đoạn thẳng AB và AC. Tìm giao tuyến của hai mặt phẳng (IBC) và (DMN)
Câu 5:
Cho tứ giác ABCD nằm trong mặt phẳng (α) có hai cạnh AB và CD không song song. Gọi S là điểm nằm ngoài mặt phẳng (α) và M là trung điểm đoạn SC.
a) Tìm giao điểm N của đường thẳng SD và mặt phẳng (MAB)
b) Gọi O là giao điểm của AC và BD. Chứng minh rằng ba đường thẳng SO, AM, BN đồng quy
10 giây suy nghĩ cấm tìm trên mạng
hồi sáng tớ đố bài này rùi dễ có trên mạng mà cấm tìm đó
Một câu hỏi quá dài , quá nhiều lại quá khó hiểu . Bạn chia thành từng bài đi cho giảm mệt!
Đúng 0
Bình luận (0)
Mặc dù chưa tìm đc cách giải nhưng mk thấy vui vì bn là người đam mê học toán, học toán hết mk và trung thực. Bn sẽ thành công. Chúc bn học giỏi.
Xem thêm câu trả lời