Cho hình vẽ :
CTR : AB // GH
chứng tỏ AB//EF trong mỗi hình sau
hình a
hình b
hình a, ta thấy
\(\angle\left(A\right)+\angle\left(DCA\right)=120+60=180^0\)
mà 2 góc này ở vị trí trong cùng phía
\(=>AB//CD\left(1\right)\)
có \(\angle\left(DCE\right)+\angle\left(E\right)=40+140=180^O\)
mà 2 góc này ở vị trí trong cùng phía
\(=>CD//EF\left(2\right)\)
(1)(2)\(=>AB//EF\)
hình b,
\(=\angle\left(BAD\right)=\angle\left(ADC\right)=30^0\)
mà 2 góc này ở vị trí so le trong \(=>AB//CD\left(1\right)\)
có \(\angle\left(CDE\right)=\angle\left(DEF\right)=40^o\)
mà 2 góc này ở vị trí so le trong \(=>CD//EF\left(2\right)\)
(1)(2)\(=>AB//EF\)
cho hình vẽ . chứng minh AB song song với CD B A E C D 100 độ 120 độ 140 độ
Hình vẽ bên, cho biết: AB // CD // EF // GH; AC = CE = EG;
BD = DF = FH; AB = x(cm); CD = 12cm; EF = y(cm); GH = 16cm.
Thế thì giá trị của x và y là:
Giải:
Hình thang CDHG có: CE = GE , DF = HF ( gt )
=> EF là đường TB của hình thang.
=> EF = \(\dfrac{CD+GH}{2}\) = \(\dfrac{12+16}{2}\) = 14 cm ( hay y = 14 cm )
Hình thang ABFE có: AC = CE, BD = DF ( gt )
=> CD là đường TB của hình thang trên.
=> CD = \(\dfrac{AB+EF}{2}\)
mà CD = 12 cm, EF = 14 cm ( cmt )
=> AB = 12.2 - 14 = 10 cm ( hay x = 10 cm )
Vậy x = 10 cm, y = 14 cm
TL
a) 5x + 20 = 110
<=> x = 90 : 5 = 18
b) x + 18 = - 13
<=> x = - 31
c) 120 - x = 50
<=> x = 70
d) 10 - x = -29
<=> x = 39
e) - x + 31 = 61
<=> x = -30
f) -85 - x = --70
<=> x = 15
Khi nào rảnh vào kênh H-EDITOR xem vid nha!!! Thanks!
Bài toán 3 : Tìm UCLN. a) ƯCLN ( 10 ; 28) e) ƯCLN (24 ; 84 ; 180) b) ƯCLN (24 ; 36) g) ƯCLN (56 ; 140) c) ƯCLN (16 ; 80 ; 176) h) ƯCLC (12 ; 14 ; 8 ; 20) d) ƯCLN (6 ; 8 ; 18) k) ƯCLN ( 7 ; 9 ; 12 ; 21)
Bài toán 4 : Tìm ƯC. a) ƯC(16 ; 24) e) ƯC(18 ; 77) b) ƯC(60 ; 90) g) ƯC(18 ; 90) c) ƯC(24 ; 84) h) ƯC(18 ; 30 ; 42) d) ƯC(16 ; 60) k) ƯC(26 ; 39 ; 48)
Bài toán 5 : Tìm BCNN của. a) BCNN( 8 ; 10 ; 20) f) BCNN(56 ; 70 ; 126) b) BCNN(16 ; 24) g) BCNN(28 ; 20 ; 30) c) BCNN(60 ; 140) h) BCNN(34 ; 32 ; 20) d) BCNN(8 ; 9 ; 11) k) BCNN(42 ; 70 ; 52) e) BCNN(24 ; 40 ; 162) l) BCNN( 9 ; 10 ; 11)
Bài toán 6 : Tìm bội chung (BC) của. a) BC(13 ; 15) e) BC(30 ; 105) b) BC(10 ; 12 ; 15) g) BC( 84 ; 108) c) BC(7 ; 9 ; 11) h) BC(98 ; 72 ; 42) d) BC(24 ; 40 ; 28) k) BC(68 ; 208 ; 100)
Please
GIúp Mình với
bạn nên chia nhỏ đề bài ra
cái này dễ mak bn ơi,bn đăng
từng bài một mn sẽ giải chứ
bn đăng như này chưa chắc
đã cs ng giải cho bn
nhìn cái này chắc loạn thị luôn ak
Câu 1: Cho tứ giác EFGHcó góc E=70 độ, F=80 độ .Tính G,H biết G-H=20 độ
câu 2: Cho hình thang ABCD (AB//CD) có góc A-B=40 độ, góc A=2 lần góc C. Tính các góc của hình thang ?
bài 2: 1, chứng minh a//b
2 chứng minh EF//GH
bài 3
a, vì sao a//b
b tính số đo các góc ở đỉnh C
Có \(\widehat{A_1}=\widehat{B_1}\)\(\Rightarrow\)a//b (Vì \(\widehat{A_1};\widehat{B_1}\) là hai góc so le trong)
Có \(\widehat{A_2}=180^0-\widehat{A_1}=180^0-120^0=60^0\)
\(\Rightarrow\widehat{A_2}=\widehat{B_1}\) mà hai góc ở vị trí đông vị \(\Rightarrow\) EF//GH
a) Ta có: \(\widehat{aAB}=b\widehat{BA}\left(=60^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên a//b(Dấu hiệu nhận biết hai đường thẳng song song)
Tìm BCNN:
a, BCNN ( 8, 10, 20 )
b, BCNN (16, 24 )
c, BCNN ( 60, 140 )
d, BCNN ( 8, 9, 11 )
e, BCNN ( 24, 40, 162 )
f, BCNN ( 56, 70, 162 )
g, BCNN (28, 30 20 )
h, BCNN ( 34, 32, 20 )
k, BCNN ( 42, 70, 52 )
I, BCNN ( 9, 10, 11 )
Ta có:8=23
10=2.5
24=24.5
BCNN(...)=23.5=24.5=40
b)Ta có:
16=24
24=23.3
BCNN(...)=24.3=48
c)Ta có:
60=22.3.5
140=22.5.7
BCNN(...)=22.3.5.7=420
Mấy bài sau bn cứ lm như thế này nhé^^
Bài toán 5: Tìm BCNN của.
a) BCNN( 8 ; 10 ; 20) f) BCNN(56 ; 70 ; 126)
b) BCNN(16 ; 24) g) BCNN(28 ; 20 ; 30)
c) BCNN(60 ; 140) h) BCNN(34 ; 32 ; 20)
d) BCNN(8 ; 9 ; 11) k) BCNN(42 ; 70 ; 52)
e) BCNN(24 ; 40 ; 162) l) BCNN( 9 ; 10 ; 11)
a) 8 = 2³
10 = 2.5
20 = 2².5
BCNN(8; 10; 20) = 2³.5 = 40
b) 16 = 2⁴
24 = 2³.3
BCNN(16; 24) = 2⁴.3 = 48
c) 60 = 2².3.5
140 = 2².5.7
BCNN(60; 140) = 2².3.5.7 = 420
d) 8 = 2³
9 = 3²
11 = 11
BCNN(8; 9; 11) = 2³.3².11 = 792
e) 24 = 2³.3
40 = 2³.5
162 = 2.3⁴
BCNN(24; 40; 162) = 2³.3⁴.5 = 3240
f) 56 = 2³.7
70 = 2.5.7
126 = 2.3².7
BCNN(56; 70; 126) = 2³.3².5.7 = 2520
g) 28 = 2².7
20 = 2².5
30 = 2.3.5
BCNN(28; 20; 30) = 2².3.5.7 = 420
h) 34 = 2.17
32 = 2⁵
20 = 2².5
BCNN(34; 32; 20) = 2⁵.5.17 = 2720
k) 42 = 2.3.7
70 = 2.5.7
20 = 2².5
BCNN(42; 70; 20) = 2².3.5.7 = 420
l) 9 = 3²
10 = 2.5
11 = 11
BCNN(9; 10; 11) = 2.3².5.11 = 990
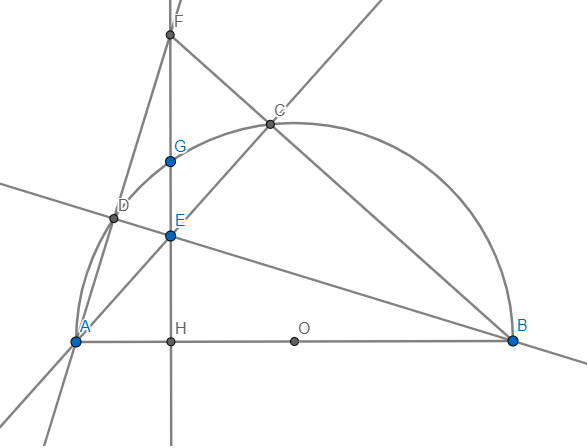
Cho nửa đường tròn (O),đường kính AB.Trên nửa đường tròn (O) lấy điểm G tùy ý (G khác A và B).Vẽ GH vuông góc với AB (H thuộc AB);trên đoạn thẳng HG lấy một điểm E (E khác H và G).Các tia AE và BE cắt nửa đường tròn (O) lần lượt tại C và D.Gọi F là giao điểm của hai tia BC và AD.Chứng minh rằng :
a)Tứ giác ECFD nội tiếp được trong một đường tròn
b)Bốn điểm H,E,G,F thẳng hàng
a) Vì AB là đường kính \(\Rightarrow\angle ADB=\angle ACB=90\)
\(\Rightarrow\angle FDE+\angle FCE=90+90=180\Rightarrow ECFD\) nội tiếp
b) GH cắt AD tại F'.F'B cắt AE tại C'
Ta có: \(\left\{{}\begin{matrix}F'H\bot AB\\BD\bot AF'\end{matrix}\right.\Rightarrow E\) là trực tâm \(\Delta F'AB\Rightarrow AE\bot F'B\Rightarrow AC'\bot F'B\)
mà AB là đường kính \(\Rightarrow C'\in\left(O\right)\Rightarrow C\equiv C'\Rightarrow F'\equiv F\Rightarrow\) đpcm