1. If you are calm, you won't make a wrong decision.
2. These wonderful poems were written by a great poet.
3.Because of rained heavily, Jane didn't go fishing yesterday.
4.Vietnamese people use Khue Van pavilion as a symbol of Hanoi.
5. His idea is not the same as me.
6. Those modern paintings are not as expensive as these Dong Ho paintings.
7. What food do you like?
8.These machines are used by chefs to mix the ingredients.
9. It i've most seen such a boring movie.
10. There are not many eggs in the fridge.
11.They started living there 2 years ago.
12. I have never drunk cocktail before.
13.This exercise is not as difficult as the last one.
14. I find playing computer games boring.
15. The new building has the same height as the old one.
16. She didn't have enough eggs to make an omelette.
17. In spite of promising that wouldn't be late, he didn't arrive until 9 o'clock.
18. 

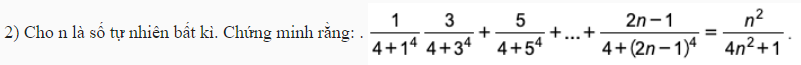
Chắc đề đúng là \(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...\)

- Với \(n=1\) đẳng thức đúng

- Giả sử đẳng thức cũng đúng với \(n=k>1\) hay:

\(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...+\dfrac{2k-1}{4+\left(2k-1\right)^4}=\dfrac{k^2}{4k^2+1}\)

- Ta cần chứng minh nó cũng đúng với \(n=k+1\) hay:

\(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...+\dfrac{2k-1}{4+\left(2k-1\right)^4}+\dfrac{2k+1}{4+\left(2k+1\right)^4}=\dfrac{\left(k+1\right)^2}{4\left(k+1\right)^2+1}\)

Thật vậy, ta có:

\(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...+\dfrac{2k-1}{4+\left(2k-1\right)^4}+\dfrac{2k+1}{4+\left(2k+1\right)^4}=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{4+\left(2k+1\right)^4}\)

\(=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{\left(2k+1\right)^4+4\left(2k+1\right)^2+4-4\left(2k+1\right)^2}=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{\left(4k^2+4k+3\right)^2-\left(4k+2\right)^2}\)

\(=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{\left(4k^2+1\right)\left(4k^2+8k+5\right)}=\dfrac{k^2\left(4k^2+8k+5\right)+2k+1}{\left(4k^2+1\right)\left(4k^2+8k+5\right)}\)

\(=\dfrac{\left(k+1\right)^2\left(4k^2+1\right)}{\left(4k^2+1\right)\left(4k^2+8k+5\right)}=\dfrac{\left(k+1\right)^2}{4k^2+8k+5}=\dfrac{\left(k+1\right)^2}{4\left(k+1\right)^2+1}\) (đpcm)

a, thay x=25 vào A ta có:

\(A=\dfrac{\sqrt{x}}{\sqrt{x}-1}=\dfrac{\sqrt{25}}{\sqrt{25}-1}=\dfrac{5}{5-1}=\dfrac{5}{4}\)

b, \(P=\dfrac{\sqrt{x}}{\sqrt{x}-1}\left(\dfrac{3x+3}{x\sqrt{x}-1}-\dfrac{2}{\sqrt{x}-1}\right)\)

\(\Rightarrow P=\dfrac{\sqrt{x}}{\sqrt{x}-1}\left(\dfrac{3x+3}{\sqrt{x^3}-1}-\dfrac{2\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right)\)

\(\Rightarrow P=\dfrac{\sqrt{x}}{\sqrt{x}-1}\left(\dfrac{3x+3}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{2x+2\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right)\)

\(\Rightarrow P=\dfrac{\sqrt{x}}{\sqrt{x}-1}.\dfrac{3x+3-2x-2\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)

\(\Rightarrow P=\dfrac{\sqrt{x}\left(x-2\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)^2\left(x+\sqrt{x}+1\right)}\)

\(\Rightarrow P=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)^2\left(x+\sqrt{x}+1\right)}\)

\(\Rightarrow P=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)

\(=2\sqrt{3}-10\sqrt{3}-\sqrt{3}+\dfrac{5\sqrt{3}}{2}=\dfrac{5\sqrt{3}}{2}-9\sqrt{3}=\dfrac{5\sqrt{3}-18\sqrt{3}}{2}=\dfrac{-13\sqrt{3}}{2}\)

\(=\dfrac{1}{2}.4\sqrt{3}-2.5\sqrt{3}-\sqrt{3}+5.\dfrac{\sqrt{3}}{2}\)

\(=2\sqrt{3}-10\sqrt{3}-\sqrt{3}+\dfrac{5\sqrt{3}}{2}\)

\(=-9\sqrt{3}+\dfrac{5\sqrt{3}}{2}=\dfrac{-18\sqrt{3}+5\sqrt{3}}{2}=-\dfrac{13\sqrt{3}}{2}\)

Giải hpt:

Đặt: \(\left[{}\begin{matrix}\sqrt{x-1}=a\\y+1=b\end{matrix}\right.\)

Ta có: \(\left\{{}\begin{matrix}3a-2b=-1\\5a-9b=-13\end{matrix}\right.< =>\left\{{}\begin{matrix}15a-10b=-5\\15a-27b=-39\end{matrix}\right.< =>\left\{{}\begin{matrix}b=2\\15a-27\cdot2=-39\end{matrix}\right.< =>\left\{{}\begin{matrix}b=2\\a=1\end{matrix}\right.\)

Thay: \(\left[{}\begin{matrix}\sqrt{x-1}=1\\y+1=2\end{matrix}\right.< =>\left[{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)

h=1,4+tan39o.400 ≈325(m)

\(A=\sqrt{2a\left(b+1\right)}+\sqrt{2b\left(c+1\right)}+\sqrt{2c\left(a+1\right)}\)

\(A=\dfrac{1}{\sqrt{2}}\sqrt{4a\left(b+1\right)}+\dfrac{1}{\sqrt{2}}\sqrt{4b\left(c+1\right)}+\dfrac{1}{\sqrt{2}}\sqrt{4c\left(a+1\right)}\)

\(A\le\dfrac{1}{2\sqrt{2}}\left(4a+b+1\right)+\dfrac{1}{2\sqrt{2}}\left(4b+c+1\right)+\dfrac{1}{2\sqrt{2}}\left(4c+a+1\right)\)

\(A\le\dfrac{1}{2\sqrt{2}}\left[5\left(a+b+c\right)+3\right]=2\sqrt{2}\)

\(A_{max}=2\sqrt{2}\) khi \(a=b=c=\dfrac{1}{3}\)

Câu 11: B

Câu 12: D

Câu 13: B

Câu 14: A

Câu 15: D