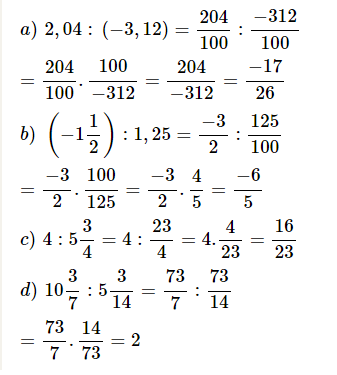Ta có :

\(\frac{2}{7}A=\frac{4}{9}\left(\frac{3}{10}B\right)\)

\(\frac{2}{7}A=\frac{2}{15}B\)

\(\frac{A}{B}=\frac{\frac{2}{15}}{\frac{2}{7}}=\frac{7}{15}\)

Vậy ...

vậy j bạn

2A/7 = (3B/10).4/9

A/B = 7/15

CÒN bài violympic nào k, mk làm tiếp cho

minh con nhieu bai violympic lam

Cách làm lớp 7: Theo bài ra ta có:

    \(\frac{\frac{2}{7}A}{\frac{3}{10}B}=\frac{4}{9}\) \(\Rightarrow\frac{A}{B}=\frac{4}{9}\times\frac{3}{10}:\frac{2}{7}=\frac{7}{15}\)

Cách làm ở bậc tiểu học: Các mẫu số : 7, 9, 10 . Ta tìm số chia hết cho tất cả các mẫu số này (để chắc chắn khi lấy phần bảy, phần chín và phần mười không dư), số đó là: 7x9x10=630.

Vậy nếu coi số B là 630 phần bằng nhau => 3/10 của B là \(\frac{3}{10}\times630=189\) phần

2/7 của A bằng: 4/9 của 189 phần và bằng \(\frac{4}{9}\times189=84\) phần

=> A bằn 7/2 của 84 phần và bằng: \(\frac{7}{2}\times84=294\) phần.

Vậy tỉ số \(\frac{A}{B}=\frac{294}{630}=\frac{294:42}{630:42}=\frac{7}{15}\)

2A/7 =(3B/10).4/9

A/B=7/15

\(A=\dfrac{4}{7.31}+\dfrac{6}{7.41}+\dfrac{9}{10.41}+\dfrac{7}{10.57}\Rightarrow\dfrac{A}{5}=\dfrac{4}{35.31}+\dfrac{6}{35.41}+\dfrac{9}{50.41}+\dfrac{7}{50.57}\)

\(\dfrac{A}{5}=\dfrac{1}{31}-\dfrac{1}{35}+\dfrac{1}{35}-\dfrac{1}{41}+\dfrac{1}{41}-\dfrac{1}{50}+\dfrac{1}{50}-\dfrac{1}{57}\)

\(\dfrac{A}{5}=\dfrac{1}{31}-\dfrac{1}{57}=\dfrac{26}{31.57}\Rightarrow A=\dfrac{130}{31.57}\)

\(\dfrac{B}{2}=\dfrac{7}{38.31}+\dfrac{5}{38.41}+\dfrac{3}{46.43}+\dfrac{11}{46.57}\Rightarrow\dfrac{B}{2}=\dfrac{1}{31}-\dfrac{1}{57}=\dfrac{26}{31.57}\)

\(\Rightarrow B=\dfrac{52}{31.57}\)

\(\dfrac{A}{B}=\dfrac{130}{31.51}:\dfrac{52}{31.57}=\dfrac{5}{2}\)

Ta có : `A:5=4/35.31+6/35.41++9/50.41+7/50.57`

`A/5 = 1/31 - 1/35 +1/35-1/41+1/41-1/50+1/50-1/57`

`A/5 =1/31-1/57` `(1)`

Lại có : `B:2=7/38.31 +5/38.43+3/46.43+11/46.57`

`B/2 =1/31-1/38+1/38-1/43+1/43-1/46+1/46-1/57`

`B/2 =1/31-1/57` `(2)`

Từ `(1)` và `(2)` `=>A/5 =B/2`

                         `=>A/B=5/2`

a) Ta có: \(A=\dfrac{4}{7\cdot31}+\dfrac{6}{7\cdot41}+\dfrac{9}{10\cdot41}+\dfrac{7}{10\cdot57}\)

\(=\dfrac{20}{31\cdot35}+\dfrac{30}{35\cdot41}+\dfrac{45}{41\cdot50}+\dfrac{35}{50\cdot57}\)

\(=5\left(\dfrac{4}{31\cdot35}+\dfrac{6}{35\cdot41}+\dfrac{9}{41\cdot50}+\dfrac{7}{50\cdot57}\right)\)

\(=5\left(\dfrac{1}{31}-\dfrac{1}{35}+\dfrac{1}{35}-\dfrac{1}{41}+\dfrac{1}{41}-\dfrac{1}{50}+\dfrac{1}{50}-\dfrac{1}{57}\right)\)

\(=5\left(\dfrac{1}{31}-\dfrac{1}{57}\right)\)

Ta có: \(B=\dfrac{7}{19\cdot31}+\dfrac{5}{19\cdot43}+\dfrac{3}{23\cdot43}+\dfrac{11}{23\cdot57}\)

\(=\dfrac{14}{31\cdot38}+\dfrac{10}{38\cdot43}+\dfrac{6}{43\cdot46}+\dfrac{22}{46\cdot57}\)

\(=2\left(\dfrac{7}{31\cdot38}+\dfrac{5}{38\cdot43}+\dfrac{3}{43\cdot46}+\dfrac{11}{46\cdot57}\right)\)

\(=2\left(\dfrac{1}{31}-\dfrac{1}{38}+\dfrac{1}{38}-\dfrac{1}{43}+\dfrac{1}{43}-\dfrac{1}{46}+\dfrac{1}{46}-\dfrac{1}{57}\right)\)

\(=2\left(\dfrac{1}{31}-\dfrac{1}{57}\right)\)

Suy ra: \(\dfrac{A}{B}=\dfrac{5\left(\dfrac{1}{31}-\dfrac{1}{57}\right)}{2\left(\dfrac{1}{31}-\dfrac{1}{57}\right)}=\dfrac{5}{2}\)

a. x²=16.4

    x²=64

vì x<0 => x= -8

b: Tỉ số giữa 48 giờ và 3,2 giờ là:

48:3,2=15:1

c: \(\dfrac{-36}{7}\cdot\dfrac{2}{3}=\dfrac{-72}{21}=\dfrac{-24}{7}\)

tỉ số của a / b là (92 - 1/9 - 2/ 10 - 3/11 - ... - 92/100) trên 1/45 + 1/50 + ... + 1/500 :)) hay ngắn tắc hơn là A/B cho nhanh :)))))))))))))))

\(A=\left(1+1+...+1\right)-\left(\dfrac{1}{9}+\dfrac{2}{10}+...+\dfrac{92}{100}\right)\)𝓒𝓸́ 92 𝓼𝓸̂́ 1

\(A=\left(1-\dfrac{1}{9}\right)+\left(1-\dfrac{2}{10}\right)+...+\left(1-\dfrac{92}{100}\right)\)

\(A=\dfrac{8}{9}+\dfrac{8}{10}+...+\dfrac{8}{100}\)

\(A=8.\left(\dfrac{1}{9}+\dfrac{1}{10}+...+\dfrac{1}{100}\right)\)

\(B=\dfrac{1}{45}+\dfrac{1}{50}+...+\dfrac{1}{500}\)

\(B=\dfrac{1}{5}.\left(\dfrac{1}{9}+\dfrac{1}{10}+...+\dfrac{1}{100}\right)\)

\(\Rightarrow\dfrac{A}{B}=\dfrac{8.\left(\dfrac{1}{9}+\dfrac{1}{10}+...+\dfrac{1}{100}\right)}{\dfrac{1}{5}.\left(\dfrac{1}{9}+\dfrac{1}{10}+...+\dfrac{1}{100}\right)}\\ \Rightarrow\dfrac{A}{B}=\dfrac{8}{\dfrac{1}{5}}=40\)

𝓥𝓪̣̂𝔂 𝓽𝓲̉ 𝓼𝓸̂́ 𝓬𝓾̉𝓪 𝓐 𝓿𝓪̀ 𝓑 𝓵𝓪̀ 40

a) \(2.04:\left(-3.12\right)=\dfrac{204}{-312}=\dfrac{-17}{26}\)

b) \(\left(-1\dfrac{1}{2}\right):1.25=\dfrac{-3}{2}:\dfrac{5}{4}=\dfrac{-3}{2}\cdot\dfrac{4}{5}=\dfrac{-12}{10}=\dfrac{-6}{5}\)

c) \(4:5\dfrac{3}{4}=4:\dfrac{23}{4}=4\cdot\dfrac{4}{23}=\dfrac{16}{23}\)

d) \(10\dfrac{3}{7}:5\dfrac{3}{14}=\dfrac{73}{7}:\dfrac{73}{14}=\dfrac{2}{1}\)