Cho hbh ABCD. gọi E là điểm đối xứng vs D qua A, gọi F là điểm đối xứng vs D qua C. CMR điểm E đ/xứng vs D qua B (2 cách)
Những câu hỏi liên quan
Cho hình bình hành ABCD .Gọi E là giao điểm đối xứng vs D qua điểm A. gọi F là điểm đối xứng với D qua điểm C.Chứng minh điểm E đối xứng vs điểm F qua B
Cho hình bình hành ABCD . Gọi E là điểm đối xứng với D qua điểm A , gọi F là điểm đối xứng với D qua điểm C . Chứng minh rằng điểm E đối xứng với điểm F qua B ( giải bằng cách 2 đường chéo bằng nhau . Em đang cần gấp mn giúp e vs ạ!!! )
Vào TKHĐ là thấy hình :)
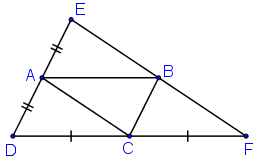
Ta có: ABCD là hình bình hành nên AB //= CD, AD//=BC.
+ E đối xứng với D qua A
⇒ AE = AD
Mà BC = AD
⇒ BC = AE.
Lại có BC // AE (vì BC // AD ≡ AE)
⇒ AEBC là hình bình hành
⇒ EB //= AC (1).
+ F đối xứng với D qua C
⇒ CF = CD
Mà AB = CD
⇒ AB = CF
Mà AB // CF (vì AB // CD ≡ CF)
⇒ ABFC là hình bình hành
⇒ AC //= BF (2)
Từ (1) và (2) suy ra E, B, F thẳng hàng và BE = BF
⇒ B là trung điểm EF
⇒ E đối xứng với F qua B
Cho hình bình hành ABCD. Gọi điểm E đối xứng vs D qua A, gọi điểm F là điểm đối xứng vs D qua C. Chứng minh rằng E đối xứng vs F quá B
Bài giải:
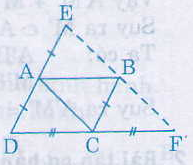
AE // BC (vì AD // BC)
AE = BC (cùng bằng AD)
nên ACBE là hình bình hành.
Suy ra: BE // AC, BE = AC (1)
Tương tự BF // AC, BF = AC (2)
Từ (1) và (2) suy ra E, B, F thẳng hàng và BE = BF. Nên B là trung điểm của EF, vậy E đối xứng với F qua B.
Đúng 0
Bình luận (0)
AE//BC (vì AD//BC)
AE=BC (cùng bằng AD)
nên ACBE là hình bình hành theo dấu hiệu nhận biết hình bình hành.
Suy ra:BE//AC,BE=AC (1)
Tương tự BF//AC,BF=AC (2)
BE và BF cùng song song với AC và cùng đi qua điểm B nên theo tiên đề Ơ -clit BE trùng BF, hay B,E,F thẳng hàng.
Từ (1) và (2) BE=BFdo đó B là trung điểm của EF
Vậy E đối xứng với F qua B
Đúng 0
Bình luận (0)
AE//BCAE//BC (vì AD//BCAD//BC)
AE=BCAE=BC (cùng bằng ADAD)
nên ACBEACBE là hình bình hành theo dấu hiệu nhận biết hình bình hành.
Suy ra: BE//AC,BE=ACBE//AC,BE=AC (1)
Tương tự BF//AC,BF=ACBF//AC,BF=AC (2)
BEBE và BFBF cùng song song với ACAC và cùng đi qua điểm BB nên theo tiên đề Ơ -clit BEBEtrùng BFBF, hay B,E,FB,E,F thẳng hàng.
Từ (1) và (2) BE=BFBE=BF do đó BB là trung điểm của EFEF.
Vậy EE đối xứng với FF qua BB.
Đúng 0
Bình luận (0)
Cho Hình bình hành ABCD. Gọi điểm E là điểm đối xứng với D qua điểm A, gọi F là điểm đối xứng với D qua điểm C. CMR điểm E đối xứng với F qua điểm B.
Giải :
AE = AD; AD = BC nên AE = BC(1)
DC = AB; DC = CF nên AB = CF (2)
GÓC EAB = BCF (Đồng vị) (3)
Từ (1); (2); (3) -> tgiac EAB = BCF (cgc) -> EB = BF (*)
Mặt khác: GÓC EBA = EFD (đồng vị); ABC = ADC (gt); CBF = AEB (đồng vị)
Cộng vế với vế: EBA + ABC + CBF = EFD + ADC + AEB
Mà EFD + ADC + AEB = 180 độ -> EBA + ABC + CBF = 180 độ (**)
Từ (*); (**) suy ra điểm E đối xứng với điểm F qua điểm B.
Đúng 0
Bình luận (0)
Cho tam giac ABC vuông tại A, đường cao AH. Gọi D là điểm đối xứng vs H qua AE ,gọi E là điểm đối xứng vs H qua AC.
a,cmr D đối xứng vs E qua A
B, Tam giác DHE là tam giac gì? Vì sao?
c, Tứ giác BDEC LÀ HÌNH GÌ? vì sao
d. Cmr BC=BD+CE
cho tứ giác abcd gọi m n p q lần lượt là trung điểm của ab bc cd da gọi e là điểm bất kỳ nằm ngoài tứ giác,f là điểm đối xứng vs e qua m g là điểm đối xứng vs f qua q ,h là điểm đối xứng vs g qua p chứng minh rằng e là điểm đối xứng vs h qua n
bạn ơi giờ bạn có đáp án chưa cho mình xin ké ạ
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua điểm A, gọi F là điểm đối xứng với D qua C. Chứng minh rằng E đối xứng với điểm F qua điểm B.
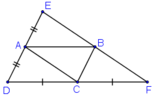
Ta có: ABCD là hình bình hành nên AB //= CD, AD//=BC.
+ E đối xứng với D qua A
⇒ AE = AD
Mà BC = AD
⇒ BC = AE.
Lại có BC // AE (vì BC // AD ≡ AE)
⇒ AEBC là hình bình hành
⇒ EB //= AC (1).
+ F đối xứng với D qua C
⇒ CF = CD
Mà AB = CD
⇒ AB = CF
Mà AB // CF (vì AB // CD ≡ CF)
⇒ ABFC là hình bình hành
⇒ AC //= BF (2)
Từ (1) và (2) suy ra E, B, F thẳng hàng và BE = BF
⇒ B là trung điểm EF
⇒ E đối xứng với F qua B
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua điểm A, gọi F là điểm đối
xứng với D qua C. Chứng minh rằng E đối xứng với điểm F qua điểm B.
Giải :
Ta có: ABCD là hình bình hành nên AB //= CD, AD//=BC.
+ E đối xứng với D qua A
⇒ AE = AD
Mà BC = AD
⇒ BC = AE.
Lại có BC // AE (vì BC // AD ≡ AE)
⇒ AEBC là hình bình hành
⇒ EB //= AC (1).
+ F đối xứng với D qua C
⇒ CF = CD
Mà AB = CD
⇒ AB = CF
Mà AB // CF (vì AB // CD ≡ CF)
⇒ ABFC là hình bình hành
⇒ AC //= BF (2)
Từ (1) và (2) suy ra E, B, F thẳng hàng và BE = BF
⇒ B là trung điểm EF
⇒ E đối xứng với F qua B
Cho tam giác vuông tại A , đường cao AH. Gọi D là điểm đối xứng vs H qua AB, E là điểm đối xứng vs H qua AC
a ,cmr D đối xứng vs E qua A
b, tam giác HDEC là tam giác gì? Vì sao?
c, tứ giác BDFE là hình gì? Chứng minh
d,cmr BC= BD+CE