Phân tích các đa thức thành nhân tử ( tách 1 hạng tử thành nhiều hạng tử)
a,x^3-19x-30
b.x^2-6x+8
 phân tích đa thức sau thành nhân tử(tách 1 hạng tử thành nhiều hạng tử)
phân tích đa thức sau thành nhân tử(tách 1 hạng tử thành nhiều hạng tử)
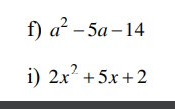 phân tích đa thức sau thành nhân tử(tách 1 hạng tử
phân tích đa thức sau thành nhân tử(tách 1 hạng tử
thành nhiều hạng tử
f, \(a^2-5a+14\) không phân tích được thành nhân tử.
i, \(2x^2+5x+2=2x^2+4x+x+2=2x\left(x+2\right)+\left(x+2\right)=\left(x+2\right)\left(2x+1\right)\)
Phân tích các đa thức sau thành nhân tử (tách một hạng tử thành nhiều hạng tử)
f) x^2-5x-14
i) x^2-7x+10
h) x^2-7x+12
g) x^2+6x+5
f)\(x^2-5x-14=x^2-7x+2x-14=x\left(x-7\right)+2\left(x-7\right)=\left(x-7\right)\left(x+2\right)\)
i)\(x^2-7x+10=x^2-2x-5x+10=x\left(x-2\right)-5\left(x-2\right)=\left(x-5\right)\left(x-2\right)\)
h)\(x^2-7x+12=x^2-3x-4x+12=x\left(x-3\right)-4\left(x-3\right)=\left(x-4\right)\left(x-3\right)\)
g)\(x^2+6x+5=x^2+x+5x+5=x\left(x+1\right)+5\left(x+1\right)=\left(x+1\right)\left(x+5\right)\)
f)\(x^2-5x-14=x^2-7x+2x-14\)
\(=\left(x+2\right)\left(x-7\right)\)
i)\(x^2-7x+10=x^2-5x-2x+10\)
\(=\left(x-2\right)\left(x-5\right)\)
h)\(x^2-7x+12=x^2-4x-3x+12\)
\(=\left(x-3\right)\left(x-4\right)\)
g)\(x^2+6x+5=x^2+x+5x+5\)
\(=\left(x+5\right)\left(x+1\right)\)
f) \(x^2-5x-14\)
\(=x^2-7x+2x-14\)
\(=\left(x^2-7x\right)+\left(2x-14\right)\)
\(=x\left(x-7\right)+2\left(x-7\right)\)
\(=\left(x+2\right)\left(x-7\right)\)
i) \(x^2-7x+10\)
\(=x^2-5x-2x+10\)
\(=\left(x^2-5x\right)-\left(2x-10\right)\)
\(=x\left(x-5\right)-2\left(x-5\right)\)
\(=\left(x-2\right)\left(x-5\right)\)
h) \(x^2-7x+12\)
\(=x^2-3x-4x+12\)
\(=\left(x^2-3x\right)-\left(4x-12\right)\)
\(=x\left(x-3\right)-4\left(x-3\right)\)
\(=\left(x-4\right)\left(x-3\right)\)
g) \(x^2+6x+5\)
\(=x^2+x+5x+5\)
\(=\left(x^2+x\right)+\left(5x+5\right)\)
\(=x\left(x+1\right)+5\left(x+1\right)\)
\(=\left(x+5\right)\left(x+1\right)\)
phân tích đa thức thành nhân tử sử dụng phương pháp tách 1 hạng tử thành nhiều hạng tử:a^4 + a^2 +1
a4 + a2 +1
= (a2)2 + 2a2 +1 -a2
= (a2 +1)2 -a2
= (a2 +1 -a)(a2 +1 +a)
Phân tích đa thức thành nhân tử bằng cách tách 1 hạng tử thành nhiều hạng tử:
3x2 + 10x + 3
\(3x^2+10x+3\)
\(=3x^2+x+9x+3\)
\(=x\left(3x+1\right)+3\left(3x+1\right)\)
\(=\left(3x+1\right)\left(x+3\right)\)
\(3x^2+10x+3=3x^2+9x+x+3=3x\left(x+3\right)+\left(x+3\right)\)
\(=\left(3x+1\right)\left(x+3\right)\)
chúc bn học tốt
3x2 + 10x +3
= 3x2 +x +9x +3 (tách 10x ra thành x+9x vì nó nhân với nhau ra 9 cộng vào ra 10)
=(3x2+x)+(9x+3)
=x(3x+1) + 3(3x+1)
=(x+3)(3x+1)
HỌC TỐT NHA BẠN !
Phân tích đa thức thành nhân tử bằng cách tách 1 hạng tử thành nhiều hạng tử :
x^2 - x - xy - 2y^2 + 2y
\(x^2-x-xy-2y^2+2y\)
\(=x^2-x-2xy+xy-2y^2+2y\)
\(=\left(-2y^2-2xy+2y\right)+\left(xy+x^2-x\right)\)
\(=2y\left(-y-x+1\right)-x\left(-y-x+1\right)\)
\(=\left(2y-x\right)\left(-y-x+1\right)\)
Phân tích đa thức thành nhân tử (tách 1 hạng tử thành nhiều hạng tử)
a) a4 + a2 + 11
b) a4 + a2 - 22
c) x4 + 4x2 - 5
Lời giải:
a. Không phân tích được thành nhân tử
b. \(a^4+a^2-22=(a^2+\frac{1}{2})^2-\frac{89}{4}=(a^2+\frac{1-\sqrt{89}}{2})(a^2+\frac{1+\sqrt{89}}{2})\)
(thông thường nhân tử là số hữu tỉ, phân tích kiểu này như cố để thành nhân tử cũng không hợp lý lắm, bạn coi lại đề)
c.
$x^4+4x^2-5=(x^4-x^2)+(5x^2-5)$
$=x^2(x^2-1)+5(x^2-1)=(x^2-1)(x^2+5)=(x-1)(x+1)(x^2+5)$
Nếu sửa như bạn nói thì làm như sau:
a.
$a^4+a^2+1=(a^2+2a^2+1)-a^2=(a^2+1)^2-a^2=(a^2+1-a)(a^2+1+a)$
b.
$a^4+a^2-2=(a^4-1)+(a^2-1)=(a^2-1)(a^2+1)+(a^2-1)$
$=(a^2-1)(a^2+1+1)=(a-1)(a+1)(a^2+2)$
Phân tích đa thức thành nhân tử bằng cách tách 1 hạng tử thành nhiều hạng tử:
x2 -10x+100
x2-10x+16=x2-8x-2x+16=(x2-8x)-(2x-16)=x(x-8)-2(x-8)=(x-8)(x-2)
Đa thức này không phân tích được đâu bạn
Cho xin mẹo: cách phân tích đa thức thành nhân tử bằng phương pháp tách 1 hạng tử thành nhiều hạng tử đối với các đa thức có bậc ba trở lên
phương pháp này mình gọi là phương pháp nhẩm nghiệm:
- Nếu tổng tất cả các hệ số bằng o thì đa thức có 1 nghiệm là x=1 hay chứa thừa số là x-1
- Nếu tổng tất cả các hệ số bậc chẵn bằng tổng các hệ số bậc lẻ thì đa thức có một nghiệm là x=-1 hay chứa thừa số là x+1