Cho tam giác ABC vuông tại A ,đường cao AH Chứng minh (AB+BC+CA)(AB-BC+CA)\(\ge4AH^2\)

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, AB = 8cm, AC = 6cm, AD là tia phân giác góc A, D ∈ BC. a) Tính DB/DC? b) Kẻ đường cao AH (H ∈ BC). Chứng minh rằng: AH/CH=AB/CA
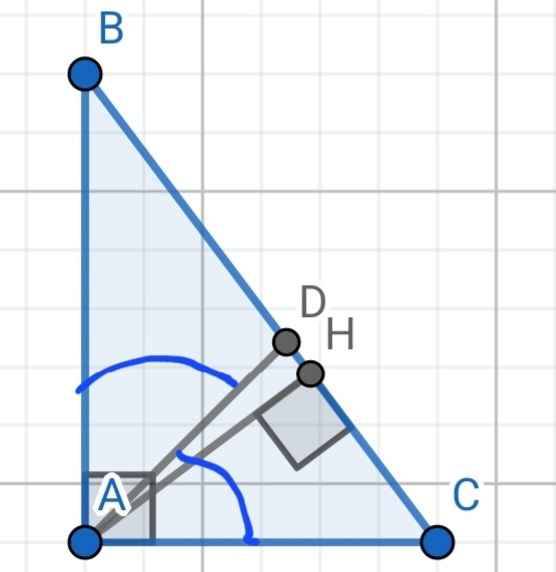
a) Do AD là phân giác của ∠A
⇒ DB/DC = 8/6 = 4/3
b) Xét hai tam giác vuông: ∆AHB và ∆CHA có:
∠HAB = ∠HCA (cùng phụ ∠B)
⇒ ∆AHB ∽ ∆CHA (g-g)
⇒ AH/CH = AB/CA
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, AB = 8cm, AC = 6cm, AD là tia phân giác góc A, D ∈ BC. a) Tính DB/DC? b) Kẻ đường cao AH (H ∈ BC). Chứng minh rằng: AH/CH=AB/CA
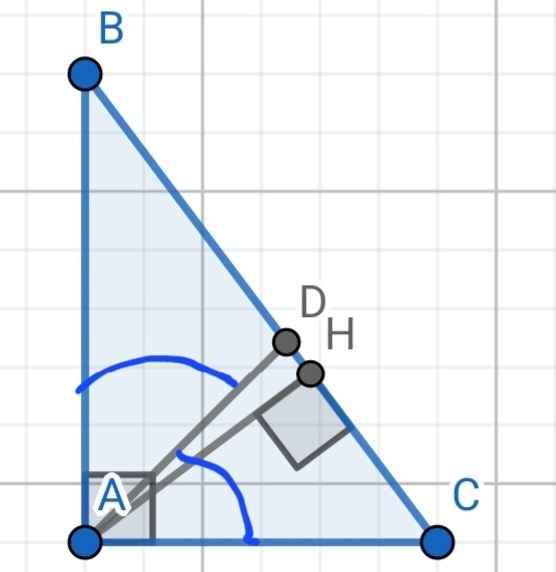
a) Do AD là phân giác của ∠A
⇒ DB/DC = 8/6 = 4/3
b) Xét hai tam giác vuông: ∆AHB và ∆CHA có:
∠HAB = ∠HCA (cùng phụ ∠B)
⇒ ∆AHB ∽ ∆CHA (g-g)
⇒ AH/CH = AB/CA
Đúng 1
Bình luận (0)
a: DB/DC=AB/AC=4/3
b: Sửa đề: AH/CA=AB/BC
\(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot AB\cdot AC\)
=>AH*BC=AB*AC
=>AH/AC=AB/CB
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A . đường cao AH . trên BC lấy M sao cho CM= CA . đường thẳng qua M song song CA cắt AB tại I .
a )tứ giác ACMI là hình gì . vì sao
b ) chứng minh rằng : 2AH + BC >AB +B
Cho tam giác ABC vuông tại A(AB<AC), vẽ đường cao AH (H thuộc BC)
a) Chứng minh tam giác ACH đồng dạng với tam giác BCA
b) Trên AC lấy điểm E sao cho AB=AE. Vẽ ED vuông góc bới BC (D thuộc BC). Chứng minh CE×CA=CD×CB
c) Chứng minh AH=HD
d) Chứng minh AD×AB=AE×BD + AB×DE
2 Cho tam giác ABC vuông ở A, AH là đường cao, M là 1 điểm trên BC sao cho CM=CA. Đường thẳng đi qua M song song với CA cắt AB tại I
a) Tứ giác ACMI là hình gì
b) Chứng minh rằng AM là phân giác của góc BAH và AI =AH
c) Chứng minh rằng AB+AC<AH+BC
2 Cho tam giác ABC vuông ở A,AH là đường cao, M là 1 điểm trên BC sao cho CM=CA. Đường thẳng đi qua M song song với CA cắt AB tại I
a) Tứ giác ACMI là hình gì
b) Chứng minh rằng AM là phân giác của góc BAH và AI=AH
c) Chứng minh rằng AB+AC<AH+BC
a) Theo đề bài ta có :
\(MI//CA\) ( GT)
=> ACMI là hình thang ( định nghĩa)
Xét hình thang ACMI ta có :
\(\widehat{A}=90^o\)
=> ACMI là hình thang vuông
Đúng 0
Bình luận (0)
1. Cho tam giác ABC vuông tại A, biết AH 16, BH 9. Tính AB.2. Cho tam giác ABC vuông tại A, AB 6cm, AC 8cm. Tính độ dài HB.3. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB 12, BC 15. Tính HC.4. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB 6, HC 9. Tính độ dài AC.5. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB 12cm, BC 16cm. Tính AH6. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB 8cm, HC 12 cm. Tính AC.
Đọc tiếp
1. Cho tam giác ABC vuông tại A, biết AH = 16, BH = 9. Tính AB.
2. Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Tính độ dài HB.
3. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 12, BC = 15. Tính HC.
4. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 6, HC = 9. Tính độ dài AC.
5. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 12cm, BC = 16cm. Tính AH
6. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 8cm, HC = 12 cm. Tính AC.
\(1,HC=\dfrac{AH^2}{BH}=\dfrac{256}{9}\\ \Rightarrow AB=\sqrt{BH\cdot BC}=\sqrt{\left(\dfrac{256}{9}+9\right)9}=\sqrt{337}\\ 2,BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\\ \Rightarrow BH=\dfrac{AB^2}{BC}=6,4\left(cm\right)\\ 3,AC=\sqrt{BC^2-AB^2}=9\\ \Rightarrow CH=\dfrac{AC^2}{BC}=5,4\\ 4,AC=\sqrt{BC\cdot CH}=\sqrt{9\left(6+9\right)}=3\sqrt{15}\\ 5,AC=\sqrt{BC^2-AB^2}=4\sqrt{7}\left(cm\right)\\ \Rightarrow AH=\dfrac{AB\cdot AC}{BC}=3\sqrt{7}\left(cm\right)\\ 6,AC=\sqrt{BC\cdot CH}=\sqrt{12\left(12+8\right)}=4\sqrt{15}\left(cm\right)\)
Đúng 1
Bình luận (3)
Câu 3. Cho ∆ABC vuông tại A (AB < AC). Về phía ngoài ∆ABC vẽ hai tam
giác ABD và tam giác ACE vuông cân ở A.
Chứng minh BC = DE.
Chứng minh BD // CE.
Kẻ đường cao AH của ∆ABC cắt DE tại M. Vẽ đường thẳng qua A và vuông
góc MC cắt BC tại N. Chứng minh rằng CA NM.
Cho tam giác ABC vuông tại A(AB<AC). Về phía ngoài tam giác ABC vẽ Tam giác ABD và Tam giác ACE cân tại A
a) Chứng minh BC=DE
b) Chứng minh BD//CE
c) Kẻ đường cao AH Của tam giác ABC cắt DE Tại M. Vẽ đường thẳng qua A và vuông góc với MC Cắt BC tại N. Chứng minh rằng CA vuông góc với NM
















