Ai chỉ giúp em chắc nghiệm với
Em cảm ơn nhiều

Những câu hỏi liên quan
Ai chỉ giúp em bài 2 ,3 với
Em cảm ơn nhiều😘
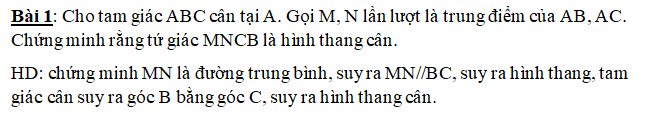
ai chỉ chi tiết giúp em vs , đc thì vẽ hình luôn nha. em cảm ơn nhiều
Xét ΔBAC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMNC là hình thang cân
Đúng 0
Bình luận (0)
ai giúp em câu hình với em cảm ơn nhiều :((

Ai giúp em giải với ạ em cảm ơn nhiều
Vì phân tử khối của A=160 đvC và có 3 nguyên tử O
=> mFe=160-3.16=102 (đvC)
=> có 2 nguyên tử Fe trong A
Ta có:PTK của B bằng 1,45 PTK của A
=> PTK của B là 160.1,45=232 (đvC)
Mà số nguyên tử Fe trong B bằng số nguyên tử O trong A
=> mO=232-3.56=64
=> có 4 nguyên tử O trong B
Đúng 2
Bình luận (1)
ai giúp em với ạ, em cảm ơn nhiều ạ;-;
Đọc tiếp
ai giúp em với ạ, em cảm ơn nhiều ạ;-;
Ai giúp em câu này với em cảm ơn nhiều.
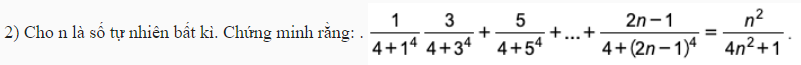
Chắc đề đúng là \(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...\)
- Với \(n=1\) đẳng thức đúng
- Giả sử đẳng thức cũng đúng với \(n=k>1\) hay:
\(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...+\dfrac{2k-1}{4+\left(2k-1\right)^4}=\dfrac{k^2}{4k^2+1}\)
- Ta cần chứng minh nó cũng đúng với \(n=k+1\) hay:
\(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...+\dfrac{2k-1}{4+\left(2k-1\right)^4}+\dfrac{2k+1}{4+\left(2k+1\right)^4}=\dfrac{\left(k+1\right)^2}{4\left(k+1\right)^2+1}\)
Thật vậy, ta có:
\(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...+\dfrac{2k-1}{4+\left(2k-1\right)^4}+\dfrac{2k+1}{4+\left(2k+1\right)^4}=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{4+\left(2k+1\right)^4}\)
\(=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{\left(2k+1\right)^4+4\left(2k+1\right)^2+4-4\left(2k+1\right)^2}=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{\left(4k^2+4k+3\right)^2-\left(4k+2\right)^2}\)
\(=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{\left(4k^2+1\right)\left(4k^2+8k+5\right)}=\dfrac{k^2\left(4k^2+8k+5\right)+2k+1}{\left(4k^2+1\right)\left(4k^2+8k+5\right)}\)
\(=\dfrac{\left(k+1\right)^2\left(4k^2+1\right)}{\left(4k^2+1\right)\left(4k^2+8k+5\right)}=\dfrac{\left(k+1\right)^2}{4k^2+8k+5}=\dfrac{\left(k+1\right)^2}{4\left(k+1\right)^2+1}\) (đpcm)
Đúng 0
Bình luận (0)
Ai giúp em với ạ, em cảm ơn rất nhiều 3
Đọc tiếp
Ai giúp em với ạ, em cảm ơn rất nhiều <3
\(\Leftrightarrow\left\{{}\begin{matrix}3x_1+x_2=-2\\x_1+x_2=2m-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x_1=-2m\\x_1+x_2=2m-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-m\\x_2=2m-2+m=3m-2\end{matrix}\right.\)
\(x_1\cdot x_2=m^2-3m\)
\(\Leftrightarrow-3m^2+2m-m^2+3m=0\)
\(\Leftrightarrow-4m^2+5m=0\)
\(\Leftrightarrow m\left(4m-5\right)=0\)
=>m=0 hoặc m=5/4
Đúng 0
Bình luận (0)
Ai giúp em câu 5,6,7 với ạ , em cảm ơn nhiều ![]()
Bài 6:
ĐK: \(9a< \dfrac{4}{a}\Leftrightarrow a^2< \dfrac{4}{9}\Leftrightarrow-\dfrac{2}{3}< a< \dfrac{2}{3}\)
Đúng 1
Bình luận (0)
Bài 7:
ĐK: \(a=\dfrac{4}{a}\Leftrightarrow a^2=4\Leftrightarrow\left[{}\begin{matrix}a=2\\a=-2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Ai giúp em câu này với em cảm ơn nhiều ạ!
Đọc tiếp
Ai giúp em câu này với em cảm ơn nhiều ạ!
a, thay x=25 vào A ta có:
\(A=\dfrac{\sqrt{x}}{\sqrt{x}-1}=\dfrac{\sqrt{25}}{\sqrt{25}-1}=\dfrac{5}{5-1}=\dfrac{5}{4}\)
b, \(P=\dfrac{\sqrt{x}}{\sqrt{x}-1}\left(\dfrac{3x+3}{x\sqrt{x}-1}-\dfrac{2}{\sqrt{x}-1}\right)\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{\sqrt{x}-1}\left(\dfrac{3x+3}{\sqrt{x^3}-1}-\dfrac{2\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right)\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{\sqrt{x}-1}\left(\dfrac{3x+3}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{2x+2\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right)\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{\sqrt{x}-1}.\dfrac{3x+3-2x-2\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(\Rightarrow P=\dfrac{\sqrt{x}\left(x-2\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)^2\left(x+\sqrt{x}+1\right)}\)
\(\Rightarrow P=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)^2\left(x+\sqrt{x}+1\right)}\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)
Đúng 6
Bình luận (1)












