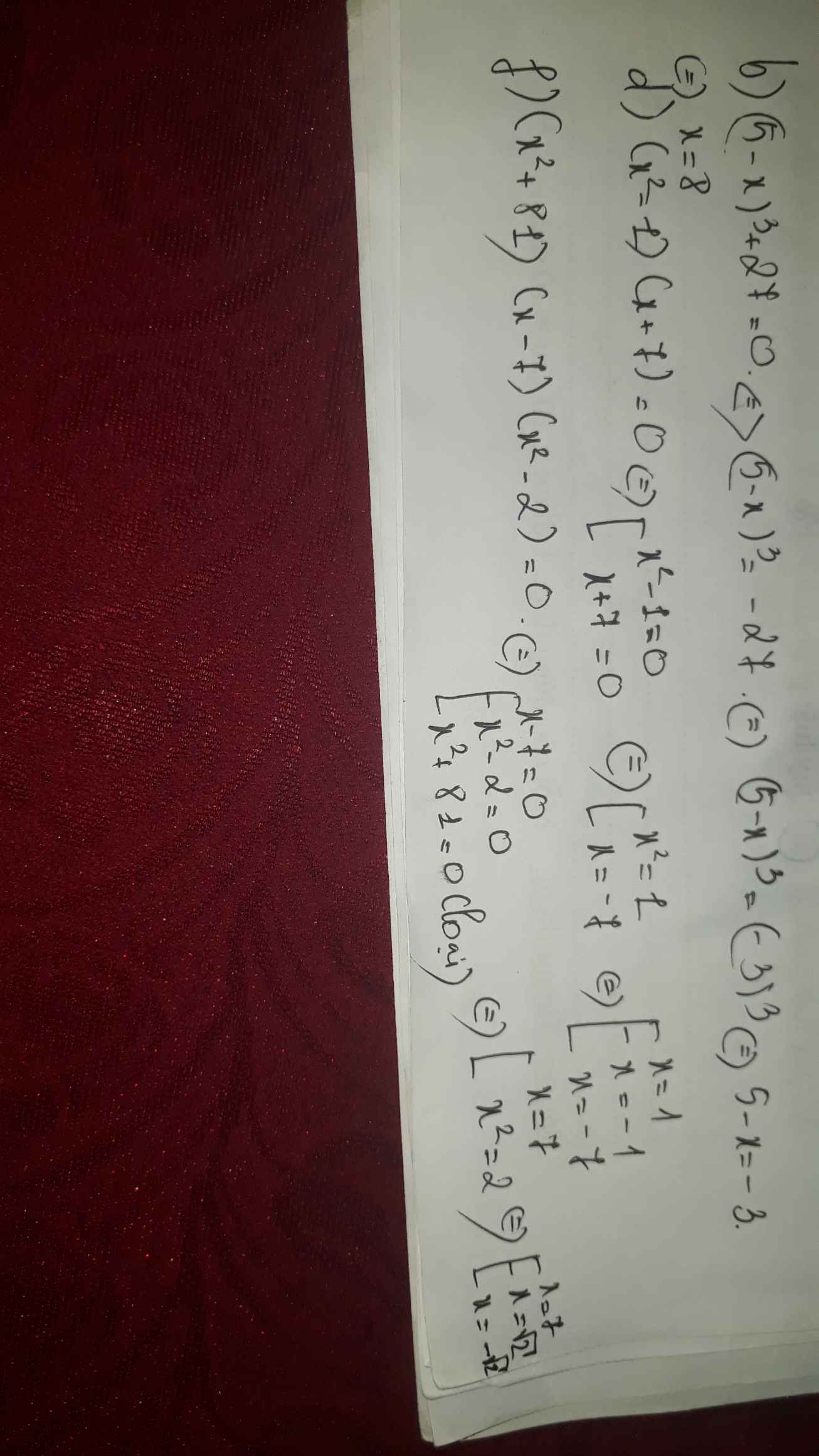Dễ thấy (\(\frac{3}{4}\)-81); (\(\frac{3^2}{5}\)-81); (\(\frac{3^3}{6}\)-81);... (\(\frac{3^{2007}}{2010}\)-81) có dạng (\(\frac{3^x}{3+x}\)-81) và x\(\varepsilon\){1;2;3;...2007}.

Nếu x=6 thì \(\frac{3^x}{3+x}\)-81=\(\frac{3^6}{3+6}\)-81=0

=>  (\(\frac{3}{4}\)-81) (\(\frac{3}{4}\)-81)(\(\frac{3^3}{6}\)-81)...​(\(\frac{3^6}{3+6}\)-81)...(\(\frac{3^{2007}}{2010}\)-81)=0

Mà |x-30|-6001=(\(\frac{3}{4}\)-81) (\(\frac{3}{4}\)-81)(\(\frac{3^3}{6}\)-81)...​(\(\frac{3^6}{3+6}\)-81)...(\(\frac{3^{2007}}{2010}\)-81)

=>|x-30|-6001=0

=>|x-30|=6001

=>x-30=6001 hoặc x-30=-6001

=>x=6031 hoặc x=-5971

-------------------The end----------------

\(\text{|x - 30| - 6001 = }\left(\frac{3}{4}-81\right)\left(\frac{3^2}{5}-81\right)\left(\frac{3^3}{6}-81\right)...\left(\frac{3^{2007}}{2010}-81\right)\)

\(\Rightarrow\text{ |x - 30| - 6001 = }\left(\frac{3}{4}-81\right)\left(\frac{3^2}{5}-81\right)\left(\frac{3^3}{6}-81\right)...\left(\frac{3^6}{9}-3^4\right)...\left(\frac{3^{2007}}{2010}-81\right)\)

\(\Rightarrow\left|x-30\right|- 6001 = \left(\frac{3}{4}-81\right)\left(\frac{3^2}{5}-81\right)\left(\frac{3^3}{6}-81\right)...\left(3^4-3^4\right)...\left(\frac{3^{2007}}{2010}-81\right)\)

\(\Rightarrow|x - 30| - 6001 = \left(\frac{3}{4}-81\right)\left(\frac{3^2}{5}-81\right)\left(\frac{3^3}{6}-81\right)...0...\left(\frac{3^{2007}}{2010}-81\right)\)

\(\Rightarrow\text{|x - 30| - 6001 = }0\)

\(\Rightarrow\left|x-30\right|=6001\) 

\(\Rightarrow x-30=6001\)hoặc \(x-30=-6001\)

\(\Rightarrow x=6031\)hoặc\(x=-5971\)

Vậy: x= 6031 hoặc x= -5971

(Nói thật thì mình mới lớp 7, đây có phải của lớp 8 không?)

a)x ∈ ∅

b) x=3

\(a,\Rightarrow2^3< 2^x\le2^4\Rightarrow x=4\\ b,\Rightarrow3^3< 3^{12}:3^x< 3^5\\ \Rightarrow3^3< 3^{12-x}< 3^5\\ \Rightarrow12-x=4\Rightarrow x=8\)

a, Ta có :  \(f\left(x\right)-g\left(x\right)=h\left(x\right)\)hay 

\(4x^2+3x+1-3x^2+2x-1=h\left(x\right)\)

\(\Rightarrow h\left(x\right)=x^2+5x\)

b, Đặt \(h\left(x\right)=x^2+5x=0\Leftrightarrow x\left(x+5\right)=0\Leftrightarrow\orbr{\begin{cases}x=0\\x=-5\end{cases}}\)

Vậy nghiệm của đa thức h(x) là x = -5 ; x = 0 

Đặt \(k\left(x\right)=7x^2-35x+42=0\)

\(\Leftrightarrow7\left(x^2+5x+6\right)=0\)

\(\Leftrightarrow7\left(x^2+2x+3x+6\right)=0\Leftrightarrow7\left(x+2\right)\left(x+3\right)=0\Leftrightarrow\orbr{\begin{cases}x=-2\\x=-3\end{cases}}\)

Vậy nghiệm của đa thức k(x) là x = -3 ; x = -2

xin lỗi mọi người 1 tý nha cái phần c) ý ạ đề thì vậy như thế nhưng có cái ở phần biểu thức ở dưới ý là 

\(\left(\frac{3^2}{6}-81\right)^3\) chuyển thành \(\left(\frac{3^3}{6}81\right)^3\)

bị sai mỗi thế thôi ạ mọi người giúp em với ạ

là \(\left(\frac{3^3}{6}-81\right)^3\)ạ

a)   2x - 17 = 3⁵ : 3²

      2x - 17 = 3^{5 - 2}

       2x - 17 = 3³ 

                      = 27

      2x        = 27 +17

       2x       = 44

         x        = 44 :2 

     vậy x = 22

b,  ( 19 - x ) .2 - 20 = 2³

                               = 8

     ( 19 - x ) .2         = 8 + 20 

     ( 19 - x ) .2         = 28

       19 - x               = 28 :2

       19 - x               = 14

              x               = 19 - 14

        vậy x              = 5

a)2x-17=243:9

2x-17=27

2x=27+17

2x=44

vậy x=44

b)(19-x).2-20=8

(19-x).2=20+8=28

19-x=28:2

19-x=14

x=19-14

x=5

vậy x=5

c)Bạn tách 3^2 thành 3^1.3^2 nhá . Tương tự tách các phần rồi rút gọn là xong .mik nhắn trên máy tính nó khó ko nhanh được ý ạ bạn thông ca,r

CHUC BAN HOC TOT

\(\left(x-2\right)^2=81\)\(\Rightarrow\orbr{\begin{cases}x-2=9\\x-2=-9\end{cases}\Rightarrow\orbr{\begin{cases}x=11\\x=-7\end{cases}}}\)

Ta có: (x-2)² =81

  <=>  (x-2)² =9²

   <=> x-2    =9

    <=> x      =9+2

    <=> x      = 11

Ta có:\(\left(x-2\right)^2=81\)

          \(\left(x-2\right)^2=9^2=\left(-9\right)^2\)

               Cái này nên dùng dấu ngoặc nhọn

            \(\Rightarrow\hept{\begin{cases}x-2=9\\x-2=-9\end{cases}\Rightarrow}\hept{\begin{cases}x=11\\x=-7\end{cases}}\)

Vậy x=11;-7

b) Ta có: \(\left(5-x\right)^3+27=0\)

\(\Leftrightarrow\left(5-x\right)^3=-27\)

\(\Leftrightarrow5-x=-3\)

hay x=8

d) Ta có: \(\left(x^2-1\right)\left(x+7\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x+7\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\\x=-7\end{matrix}\right.\)

f) Ta có: \(\left(x^2+81\right)\left(x-7\right)\left(x^2-2\right)=0\)

\(\Leftrightarrow\left(x-7\right)\left(x+\sqrt{2}\right)\left(x-\sqrt{2}\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=7\\x=\sqrt{2}\\x=-\sqrt{2}\end{matrix}\right.\)

Do \(\left|x-\dfrac{2}{3}\right|\ge0;\forall x\)

Mà \(-\dfrac{26}{\sqrt{81}}< 0\)

\(\Rightarrow\) Không tồn tại x để \(\left|x-\dfrac{2}{3}\right|< -\dfrac{26}{\sqrt{81}}\)

Hay ko tồn tại số nguyên x thỏa mãn đề bài

Bài 2: 

x=13 nên x+1=14

\(f\left(x\right)=x^{14}-x^{13}\left(x+1\right)+x^{12}\left(x+1\right)-...+x^2\left(x+1\right)-x\left(x+1\right)+14\)

\(=x^{14}-x^{14}-x^{13}+x^{13}-...+x^3+x^2-x^2-x+14\)

=14-x=1

x=13 nên x+1=14

f(x)=x14−x13(x+1)+x12(x+1)−...+x2(x+1)−x(x+1)+14f(x)=x14−x13(x+1)+x12(x+1)−...+x2(x+1)−x(x+1)+14

=x14−x14−x13+x13−...+x3+x2−x2−x+14=x14−x14−x13+x13−...+x3+x2−x2−x+14

=14-x=1