Tham Khảo:

https://olm.vn/hoi-dap/detail/86010246553.html

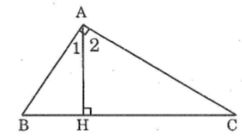
Có thể tìm góc B bằng hai cách:

Cách 1

Ta có: ∠(A1 ) + ∠(A2 ) = ∠(BAC) = 90o(1)

Vì ΔAHB vuông tại H nên:

∠B + ∠(A1) = 90o(tính chất tam giác vuông) (2)

Từ (1) và (2) suy ra ∠B = ∠(A2 )

Cách 2

Vì ΔABC vuông tại A nên:

∠B +∠C = 90o (theo tính chất tam giác vuông) (1)

Vì ΔAHC vuông tại H nên:

∠(A2 ) + ∠C = 90o (tính chất tam giác vuông) (2)

Từ (1) và (2) suy ra: ∠B = ∠(A2)

Có thể tìm góc B bằng hai cách:

Cách 1

Ta có: ∠(A1 ) + ∠(A2 ) = ∠(BAC) = 90o(1)

Vì ΔAHB vuông tại H nên:

∠B + ∠(A1) = 90o(tính chất tam giác vuông) (2)

Từ (1) và (2) suy ra ∠B = ∠(A2 )

Cách 2

Vì ΔABC vuông tại A nên:

∠B +∠C = 90o (theo tính chất tam giác vuông) (1)

Vì ΔAHC vuông tại H nên:

∠(A2 ) + ∠C = 90o (tính chất tam giác vuông) (2)

Từ (1) và (2) suy ra: ∠B = ∠(A2)

đề kiểm tra 1 tiết toán hình nè bà con

ai xem rồi thì tick zùm mình nha

Tam giác ABC vuông tại A  góc B + góc C = 90 độ

Tam giác AHB vuông tại H  góc B + góc BAH = 90 độ

Suy ra góc C = góc BAH (cùng phụ góc B)

đó là a

a,

Tam giác ABC vuông tại A nên

Tam giác AHC vuông tại H nên

b,

Chứng minh tương tự phần a ta có:

Ta có:

góc BAH + góc HAC= 90độ (tam giác ABC vuông tại H)

Mà góc BAH + góc ABH =90độ (tam giác ABH vuông tại H)

=>góc ABH= góc HAC

Vậy góc B = góc HAC

cái tam giác mik vẽ là tam giác vuông cân nên góc B = góc C

nếu là tam giác thường thì khi đó:
kẻ đường thẳng sog song với AB đí qua H cắt AC tại K ( theo hibhf vẽ)

khi đó theo tính chất 2 đường thẳng song song sẽ có HK // BA

mà BA vuông góc tại AC( tam giác ABC vuông tại A)

=> HK vuông góc với AC

theo tính chất đồng vị  => góc B = góc CHK

Hình tự vẽ

Xét tam giác ABC có \(\widehat{A}=90^o=>\widehat{B}+\widehat{C}=90^o\)

Xét tam giác HAC có \(\widehat{AHC}=90^o=>\widehat{C}+\widehat{HAC}=90^o\)

Từ 2 điều trên => \(\widehat{B}=\widehat{HAC}\)

a) Sửa đề: Trên HC lấy E sao cho HE=HB và c/m ΔBHA=ΔEHA

Xét ΔBHA vuông tại H và ΔEHA vuông tại H có 

AH chung

BH=EH(gt)

Do đó: ΔBHA=ΔEHA(hai cạnh góc vuông)

a) Sửa đề: Trên HC lấy E sao cho HE=HB 

tam giác BHA=tam giác EHA(c.g.c)

tam giác BDA=tam giác BDE(ch-gn)

suy ra góc A=góc E=90 độ và AD=ED

suy ra DE vuông góc với BC 

Áp dung định lí pitago vào tam giác DEC có góc E=90 độ

DC^2=DE^2+CE^2

suy ra DC > DE

mà DE = DA 

suy ra DC>DA

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có

AB=AC
AH chung

Do đó: ΔAHB=ΔAHC

b: Xét ΔAHM vuông tại M và ΔAHN vuông tại N có

AH chung

\(\widehat{MAH}=\widehat{NAH}\)

Do đó: ΔAHM=ΔAHN

Suy ra: AM=AN

hay ΔAMN cân tại A

c: Ta có: AM=AN

HM=HN

Do đó: AH là đường trung trực của MN

hay AH⊥MN

Xét ΔAHB vuông tại H và ΔAHC vuông tại H có

cạnh AH chung

AB=AC(vì tam giác ABC cân tại A)

=> ΔAHB=ΔAHC(c.h-c.g.v)

 Xét ΔAHM vuông tại M và ΔAHN vuông tại N có

\(\widehat{HAM}=\widehat{HAN}\)

cạnh AH chung

==> ΔAHM=ΔAHN(c.h-g.n)

==> AM=AN

=> ΔAMN cân tại A ( dấu hiệu)

c)Ta có:HM=HN   ;  AM=AN

===>AH là đường trung trực của MN

=>\(\text{AH⊥MN}\)

a) Xét tứ giác EAFH có 

\(\widehat{AFH}=90^0\)

\(\widehat{FAE}=90^0\)

\(\widehat{AEH}=90^0\)

Do đó: EAFH là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)

b) Ta có: \(\widehat{IAC}=90^0-\widehat{AFE}\)

\(\widehat{ICA}=90^0-\widehat{B}\)

mà \(\widehat{AFE}=\widehat{B}\left(=\widehat{HAC}\right)\)

nên \(\widehat{IAC}=\widehat{ICA}\)

mà \(\widehat{IBA}=90^0-\widehat{ICA}\)

và \(\widehat{IAB}=90^0-\widehat{IAC}\)

nên \(\widehat{IAB}=\widehat{IBA}\)

Xét ΔIAB có \(\widehat{IAB}=\widehat{IBA}\)(cmt)

nên ΔIAB cân tại I(Định lí đảo của tam giác cân)

Xét ΔIAC có \(\widehat{IAC}=\widehat{ICA}\)(cmt)

nên ΔIAC cân tại I(Định lí đảo của tam giác cân)

Ta có: IA=IB(ΔIAB cân tại I)

IA=IC(ΔIAC cân tại I)

Do đó: IB=IC

mà I nằm giữa B và C

nên I là trung điểm của BC(Đpcm)