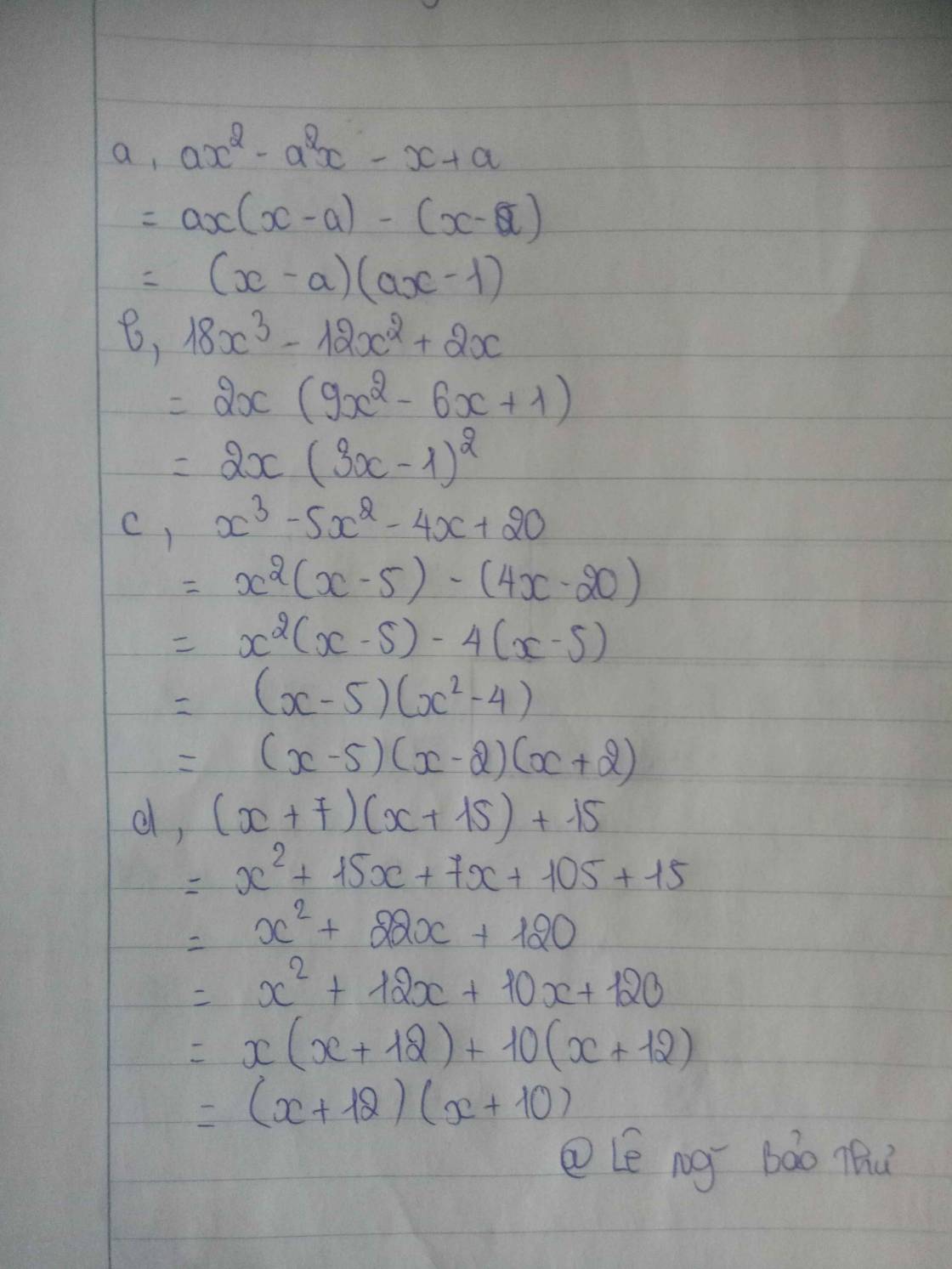=(x^2+8x)^2+23(x^2+8x)+135

Cái này ko phân tích được nha bạn

\(\left(x^2+8x+8\right)\left(x^2+8x+15\right)+15\\ \Leftrightarrow\left(x^4+8x^3+15x^2+8x^3+64x^2+120x+8x^2+64x+120\right)+15\\ \Leftrightarrow x^4+16x^3+87x^2+184x+135\)

Gọi `A=(x^2+8x+8)(x^2+8x+15)+15`

Đặt `t=x^2+8x+11,5`

`=>A=(t-3,5)(t+3,5)+15=t^2-3,5^2+15=t^2-2,75=(t-sqrt(2,75))(t+sqrt(2,75))=(x^2+8x+11,5-(sqrt11)/2)(x^2+8x+11,5+(sqrt11)/2)=(x^2+8x+(23-\sqrt11)/2)(x^2+8x+(23+\sqrt11)/2)`

c) Đặt \(A=\left(x^2+3x+1\right)\left(x^2+3x+2\right)-6\)

Đặt \(x^2+3x+1,5=a\)

\(\Rightarrow A=\left(a-0,5\right)\left(a+0,5\right)-6\)

\(\Rightarrow A=a^2-0,25-6\)

\(\Rightarrow A=a^2-\frac{25}{4}\)

\(\Rightarrow A=\left(a-\frac{5}{2}\right)\left(a+\frac{5}{2}\right)\)

Thay \(a=x^2+3x+0,5\)vào A ta có :

\(A=\left(x^2+3x+0,5-\frac{5}{2}\right)\left(x^2+3x+0,5+\frac{5}{2}\right)\)

\(A=\left(x^2+3x-2\right)\left(x^2+3x+3\right)\)

c, Đặt \(x^2+3x+2=a\)

Ta có : \(\left(a-1\right)a-6=a^2-a-6=\left(a^2-3a\right)+\left(2a-6\right)\)

                                                                       \(=a\left(a-3\right)+2\left(a-3\right)\)

                                                                       \(=\left(a+2\right)\left(a-3\right)\)

                                                                        \(=\left(x^2+3x+4\right)\left(x^2+3x-1\right)\)

Câu d làm tương tự .

Gợi ý : (x+3)(x+5) = x² + 8x + 15 

đặt bằng a rồi giải tiếp

d) Đặt \(B=\left(x^2+8x+7\right)\left(x+3\right)\left(x+5\right)+15\)

\(B=\left(x^2+8x+7\right)\left(x^2+5x+3x+15\right)+15\)

\(B=\left(x^2+8x+7\right)\left(x^2+8x+15\right)+15\)

Đặt \(a=x^2+8x+11\)

\(\Rightarrow B=\left(a-4\right)\left(a+4\right)+15\)

\(\Rightarrow B=a^2-16+15\)

\(\Rightarrow B=a^2-1\)

\(\Rightarrow B=\left(a-1\right)\left(a+1\right)\)

Thay \(a=x^2+8x+11\)vào B ta có :

\(B=\left(x^2+8x+11-1\right)\left(x^2+8x+11+1\right)\)

\(B=\left(x^2+8x+10\right)\left(x^2+8x+12\right)\)

(x+1)(x+3)(x+5)(x+8)+15

=[(x+1)(x+7)][(x+3)(x+5)]+15

=(x²+8x+7)(x²+8x+15)+15

Đặt t=x²+8x+7

=>x²+8x+15=t+8

=>(x² +8x+7)(x²+8x+15)+15

=t(t+8)+15

=t²+8t+15

=t²+3t+5t+15

=t(t+3)+5(t+3)

=(t+3)(t+5)

=(x²+8x+10)(x²+8x+12)

Đặt \(A=\left(x+1\right)\left(x+3\right)\left(x+5\right)\left(x+7\right)+15\)

\(\Rightarrow A=\left(x+1\right)\left(x+7\right)\left(x+3\right)\left(x+5\right)+15\)

        \(=\left(x^2+8x+7\right)\left(x^2+8x+15\right)+15\)

Đặt \(x^2+8x+11=t\)

\(\Rightarrow A=\left(t-4\right)\left(t+4\right)+15=t^2-16+15=t^2-1=\left(t+1\right)\left(t-1\right)\)

\(=\left(x^2+8x+11+1\right)\left(x^2+8x+11-1\right)=\left(x^2+8x+12\right)\left(x^2+8x+10\right)\)

\(=\left(x^2+2x+6x+12\right)\left(x^2+8x+10\right)\)\(=\left[x\left(x+2\right)+6\left(x+2\right)\right]\left(x^2+8x+10\right)\)

\(=\left(x+2\right)\left(x+6\right)\left(x^2+8x+10\right)\)

b)(x²+x+1)(x²+x+2)-12

Đặt t=x²+x+1

t(t+1)-12=t²+t-12

=(t-3)(t+4)=(x²+x+1-3)(x²+x+1+4)

=(x²+x-2)(x²+x+5)

=(x-1)(x+2)(x²+x+5)

c)(x²+8x+7)(x²+8x+15)+15

Đặt t=x²+8x+7 

t(t+8)+15=t²+8t+15

=(t+3)(t+5)

=(x²+8x+7+3)(x²+8x+7+15)

=(x²+8x+10)(x²+8x+22)

d)(x+2)(x+3)(x+4)(x+5)-24

=(x²+7x+10)(x²+7x+12)-24

Đặt t=x²+7x+10

t(t+2)-24=(t-4)(t+6)

=(x²+7x+10-4)(x²+7x+10+6)

=(x²+7x+6)(x²+7x+16)

=(x+1)(x+6)(x²+7x+16)

a/ Đặt x² + 4x + 8 = a

Thì đa thức ban đầu thành

a² + 3ax + 2x² = (a² + 2ax + x²) + (ax + x²)

= (a + x)² + x(a + x) = (a + x)(a + 2x)

b/ Đặt x² + x + 1 = a thì đa thức ban đầu thành

a(a + 1) - 12 = a² + a - 12 = (a² - 3a) + (4a - 12) 

= (a - 3)(a + 4)

Đặt \(x^2-8x+4=t\)

Ta có:\(A=\left(t-2\right)\left(t+2\right)-5=t^2-4-5=t^2-9=\left(t-3\right)\left(t+3\right)\)

Hay \(A=\left(x^2-8x+1\right)\left(x^2-8x+7\right)\)

\(A=\left(x^2-8x+1\right)\left(x-7\right)\left(x-1\right)\)

Cái này nếu phân tích thành nhân tử tiếp thì phức tạp lắm,bạn để như thế này thì gọn hơn

Nếu phân tích ra thì được như thế này:

\(x^2-8x+1=-\left(x+\sqrt{10}+4\right)\left(x+\sqrt{10}-4\right)\)

Đặt a=x²+3x+5 

ta có \(8a^2+7a-15\)

\(=8a^2-8a+15a-15=8a\left(a-1\right)+15\left(a-1\right)\)

\(=\left(8a+15\right)\left(a-1\right)\)

Trả lại biến

\(\left(8x^2+24x+40+15\right)\left(x^2+3x+5-1\right)\)

\(=\left(8x^2+24x+55\right)\left(x^2+3x+4\right)\)

Lời giải:

a. 

$(xy)^2-xy-2=(x^2y^2+xy)-(2xy+2)$

$=xy(xy+1)-2(xy+1)=(xy+1)(xy-2)$

b. Bạn xem lại đoạn $-16x^2$ là dấu - hay + vậy?

vài câu khó quá 

a)\(a\left(b^3-c^3\right)+b\left(c^3-a^3\right)+c\left(a^3-b^3\right)\)

\(=a\left(b^3-c^3\right)-b\text{[}\left(b^3-c^3\right)+\left(a^3-b^3\right)\text{]}+c\left(a^3-b^3\right)\)

\(=a\left(b^3-c^3\right)-b\left(b^3-c^3\right)-b\left(a^3-b^3\right)+c\left(a^3-b^3\right)\)

\(=\left(a-b\right)\left(b^3-c^3\right)-\left(b-c\right)\left(a^3-b^3\right)\)

\(=\left(a-b\right)\left(b-c\right)\left(b^2+bc+c^2\right)-\left(b-c\right)\left(a-b\right)\left(a^2+ab+b^2\right)\)

\(=\left(a-b\right)\left(b-c\right)\left(bc+c^2-a^2-ab\right)\)

\(=\left(a-b\right)\left(b-c\right)\left(c-a\right)\left(a+b+c\right)\)

\(a.\) \(ax^2-a^2x-x+a\)

\(=\left(ax^2-a^2x\right)-\left(x-a\right)\)

\(=ax\left(x-a\right)-\left(x-a\right)\)

\(=\left(ax-1\right)\left(x-a\right)\)

\(b.\) \(18x^3-12x^2+2x\)

\(=2x\left(9x^2-6x+1\right)\)

\(=2x\left(3x-1\right)^2\)

\(c.\) \(x^3-5x^2-4x+20\)

\(=\left(x^3-5x^2\right)-\left(4x-20\right)\)

\(=x^2\left(x-5\right)-4\left(x-5\right)\)

\(=\left(x^2-4\right)\left(x-5\right)\)

\(=\left(x-2\right)\left(x+2\right)\left(x-5\right)\)

\(d.\) \(\left(x+7\right)\left(x+15\right)+15\)

\(=x^2+15x+7x+105+15\)

\(=x^2+22x+120\)

\(=\left(x+10\right)\left(x+12\right)\)