E= x4+bx3cx2+dx+e với a+d=b+e=c
Chứng minh: E=(x2+x+1)[ax2+(b-a).x+c-d]
Phân tích
a,(x2 + x + 2)3 - (x+1)3 = x6 +1 b,(x2 + 10x + 8)2 - (8x + 4)(x2 + 8x+7)
c, A= x4 + 2x3 + 3x2 + 2x+4 d,B= x4 + 4x3 + +8x2 + 8x + 4
e, C= x4 - 2x3 + 5x2 - 4x + 4
Tìm m : x6 - x4 + x2 + m : x2 - 1 = B(x)(dư 0)
A) -2 B) -1 C) 0 D) 1 E)2
Lời giải:
$x^6-x^4+x^2+m=x^4(x^2-1)+(x^2-1)+m+1$
$=(x^2-1)(x^4+1)+m+1$. Như vậy, đa thức này chia cho $x^2-1$ dư $m+1$
Vì $x^6-x^4+x^2+m$ chia hết cho $x^2-1$ nên $m+1=0$
$\Leftrightarrow m=-1$
Đáp án B.
Cho hàm số y = f(x) = ax4 + bx3 + cx2 + dx + e (a≠0) có đồ thị (C) cắt trục hoành tại bốn điểm phân biệt là A(x1; 0), B(x2 ; 0), C(x3 ; 0), D(x4;0), với x1, x2, x3, x4 theo thứ tự lập thành cấp số cộng và hai tiếp tuyến của (C) tại A, B vuông góc với nhau. Tính giá trị của biếu thức S = (f ' (x3) + f ' (x4))2020
Do \(f\left(x\right)=ax^4+bx^3+cx^2+dx+e\) có 4 nghiệm pb \(x_1;x_2;x_3;x_4\)
\(\Rightarrow f\left(x\right)=a\left(x-x_1\right)\left(x-x_2\right)\left(x-x_3\right)\left(x-x_4\right)\)
Ta có:
\(f'\left(x\right)=a\left[\left(x-x_1\right)\left(x-x_2\right)\left(x-x_3\right)+\left(x-x_2\right)\left(x-x_3\right)\left(x-x_4\right)+\left(x-x_1\right)\left(x-x_3\right)\left(x-x_4\right)+\left(x-x_1\right)\left(x-x_2\right)\left(x-x_4\right)\right]\)
\(\Rightarrow\left\{{}\begin{matrix}f'\left(x_1\right)=a\left(x_1-x_2\right)\left(x_1-x_3\right)\left(x_1-x_4\right)\\f'\left(x_2\right)=a\left(x_2-x_1\right)\left(x_2-x_3\right)\left(x_2-x_4\right)\\f'\left(x_3\right)=a\left(x_3-x_1\right)\left(x_3-x_2\right)\left(x_3-x_4\right)\\f'\left(x_4\right)=a\left(x_4-x_1\right)\left(x_4-x_2\right)\left(x_4-x_3\right)\end{matrix}\right.\)
Mà tiếp tuyến tại A và B vuông góc \(\Leftrightarrow f'\left(x_1\right).f'\left(x_2\right)=-1\) (1)
Do \(x_1;x_2;x_3;x_4\) lập thành 1 CSC, giả sử công sai của CSC là \(d\)
\(\Rightarrow\left\{{}\begin{matrix}x_2=x_1+d\\x_3=x_1+2d\\x_4=x_1+3d\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}f'\left(x_1\right)=a.\left(-d\right).\left(-2d\right).\left(-3d\right)=-6ad^3\\f'\left(x_2\right)=a.d.\left(-d\right).\left(-2d\right)=2ad^3\\f'\left(x_3\right)=a.2d.d.\left(-d\right)=-2ad^3\\f'\left(x_4\right)=a.3d.2d.d=6ad^3\end{matrix}\right.\)
Thế vào (1): \(-12a^2d^6=-1\Leftrightarrow12a^2d^6=1\)
\(\Rightarrow f'\left(x_3\right)+f'\left(x_4\right)=4ad^3\)
\(\Rightarrow S=\left(4ad^3\right)^{2020}=\left(16a^2d^6\right)^{1010}=\left(\dfrac{4}{3}.12a^2d^6\right)^{1010}=\left(\dfrac{4}{3}\right)^{1010}\)
Bài gì mà dễ sợ :(
Đầu tiên xác định cụ thể pt (P) ra:
(P) qua điểm \(\left(0;-3\right)\Rightarrow c=-3\)
Từ độ độ đỉnh: \(\left\{{}\begin{matrix}-\dfrac{b}{2a}=2\\\dfrac{4ac-b^2}{4a}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-4a\\-12a-16a^2=4a\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-1\\b=4\end{matrix}\right.\)
\(\Rightarrow y=-x^2+4x-3\)
\(\Rightarrow y'=-2x+4\)
Gọi giao điểm của \(d_1;d_2\) là A và giao điểm của \(d_1;d_2\) với Ox lần lượt là B và C \(\Rightarrow\Delta ABC\) vuông cân tại A (\(y'=-2x+4\) nên (P) không thể tồn tại 1 tiếp tuyến vuông góc trục hoành dạng \(x=k\) do đó 2 tiếp tuyến ko bao giờ vuông góc với Ox)
\(\Rightarrow AB\) tạo với trục hoành 1 góc 45 độ
\(\Rightarrow\) Hệ số góc của đường thẳng \(d_1\) là \(k=tan45^0=1\)
\(\Rightarrow y'=-2x+4=1\Rightarrow x=\dfrac{3}{2}\)
\(\Rightarrow y=\dfrac{3}{4}\)
Phương trình \(d_1\): \(y=1\left(x-\dfrac{3}{2}\right)+\dfrac{3}{4}\Leftrightarrow y=x-\dfrac{3}{4}\)
Bài 1: Tìm đa thức M biết : M-3xyz+5x2-7xy+9=6x2+xyz+2xy+3-y2
Bài 2: Chứng minh đa thức sau vô nghiệm :
a)ax2+2x+3 b)x2+4x+6
Bài 3: Cho đa thức P(x)= ax4+bx3+cx2+dx+e, biết P(1)=P(-1) , P(2)=P(-2).
Chứng minh P(x)=P(-x) với mọi x
( giúp mình nha cảm ơn mọi người aa<3 )
Bài 2:
a: Sửa đề: \(x^2+2x+3\)
Đặt \(x^2+2x+3=0\)
\(\Delta=2^2-4\cdot1\cdot3=4-12=-8< 0\)
Do đó: Phương trình vô nghiệm
b: Đặt \(x^2+4x+6=0\)
\(\Leftrightarrow x^2+4x+4+2=0\)
\(\Leftrightarrow\left(x+2\right)^2+2=0\)(vô lý)
Giải hộ e bài này với ai 👍
Câu 1 : a, 4x2 -3x-1=0 / d, 4x4-5x2+1=0
b, x2 - (1+căn 5)x + căn 5= 0 / e,x2 +3=|4x| / f, 2x + 5cănx +3 =0 / g, (x2 +x +1 ).(x2+x+2)=2 / h, x4-5x2+4=0
c, x4 + x2 -20=0 / k, x phần x2-1 -- 1 phần 2(x+1) = 1phan 2
1. Cho đa thức f(x)ϵZ[x]f(x)ϵZ[x]
f(x)=ax4+bx3+cx2+dx+ef(x)=ax4+bx3+cx2+dx+e với a, b, c, d, e là các số lẻ.
Cm đa thức không có nghiệm hữu tỉ
2. Cho P(x) có bậc 3; P(x)ϵZ[x]P(x)ϵZ[x] và P(x) chia hết cho 7 với mọi x ϵZϵZ
CmR các hệ số của P(x) chia hết cho 7.
3. Cho đa thức P(x) bậc 4 có hệ số cao nhất là 1 thỏa mãn P(1)=10; P(2)=20; P(3)=30.
Tính P(12)+P(−8)10P(12)+P(−8)10
4. Tìm đa thức P(x) dạng x5+x4−9x3+ax2+bx+cx5+x4−9x3+ax2+bx+c biết P(x) chia hết cho (x-2)(x+2)(x+3)
5. Tìm đa thức bậc 3 có hệ số cao nhất là 1 sao cho P(1)=1; P(2)=2; P(3)=3
6. Cho đa thức P(x) có bậc 6 có P(x)=P(-1); P(2)=P(-2); P(3)=P(-3). CmR: P(x)=P(-x) với mọi x
7. Cho đa thức P(x)=−x5+x2+1P(x)=−x5+x2+1 có 5 nghiệm. Đặt Q(x)=x2−2.Q(x)=x2−2.
Tính A=Q(x1).Q(x2).Q(x3).Q(x4).Q(x5)A=Q(x1).Q(x2).Q(x3).Q(x4).Q(x5) (x1,x2,x3,x4,x5x1,x2,x3,x4,x5 là các nghiệm của P(x))
Cho f ( x ) = x 3 + a x 2 + b x + c và g ( x ) = f ( d x + e ) với a , b , c , d , e ∈ ℝ có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số y=f(x) Diện tích hình phẳng giới hạn bởi hai đường congy=f(x) và y=g(x) gần nhất với kết quả nào dưới đây?
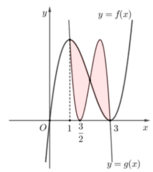
A. 4,5
B. 4,25
C. 3,63
D. 3,67
Xác định giá trị a, b, c để hàm số F ( x ) = ( a x 2 + b x + c ) e - x là một nguyên hàm của f ( x ) = ( x 2 - 3 x + 2 ) e - x
A. a = -1; b = 1; c = -1
B. a = -1; b = -5; c = -7
C. a = 1; b = -3; c = 2
D. a = 1; b = -1; c = 1
cho đa thức f(x) = ax4 + bx3 + cx2 + dx + e với a,b,c,d,e ∈ Z và a ≠ 0. Biết rằng f(x) ⋮ 7 với mọi giá trị x nguyên. Chứng minh rằng các hệ số của đa thức trên đều chia hết cho 7
f(0) ⋮ 7 => e ⋮ 7
=> g(x) = ax4 + bx3 + cx2 + dx ⋮ 7 ∀ x nguyên
g(1) = a + b + c + d ⋮ 7
g(-1) = a - b + c - d ⋮ 7
=> \(\left\{{}\begin{matrix}\left(a+b+c+d\right)+\left(a-b+c-d\right)⋮7\\\left(a+b+c+d\right)-\left(a-b+c-d\right)⋮7\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}2\left(a+c\right)⋮7\\2\left(b+d\right)⋮7\end{matrix}\right.\)
Mà 2 không chia hết cho 7 => \(\left\{{}\begin{matrix}a+c⋮7\\b+d⋮7\end{matrix}\right.\) (1)
g(2) = 16a + 8b + 4c + 2d ⋮ 7
g(-2) = 16a - 8b + 4c - 2d ⋮ 7
=> \(\left\{{}\begin{matrix}\left(16a+8b+4c+2d\right)+\left(16a-8b+4c-2d\right)⋮7\\\left(16a+8b+4c+2d\right)-\left(16a-8b+4c-2d\right)⋮7\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}8\left(4a+c\right)⋮7\\4\left(4b+d\right)⋮7\end{matrix}\right.\)
Mà 8 và 4 không chia hết cho 7
=> \(\left\{{}\begin{matrix}4a+c⋮7\\4b+d⋮7\end{matrix}\right.\) (2)
Từ (1) và (2)
=> \(\left\{{}\begin{matrix}\left(4a+c\right)-\left(a+c\right)⋮7\\\left(4b+d\right)-\left(b+d\right)⋮7\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}3a⋮7\\3b⋮7\end{matrix}\right.\)
Mà 3 không chia hết cho 7 => \(\left\{{}\begin{matrix}a⋮7\\b⋮7\end{matrix}\right.\)
Lại có: \(\left\{{}\begin{matrix}a+c⋮7\\b+d⋮7\end{matrix}\right.\) => \(\left\{{}\begin{matrix}c⋮7\\d⋮7\end{matrix}\right.\)
Vậy bài toán đã được chứng minh