Đk:\(-4\le x\le1.\)

Đặt \(\sqrt{1-x}=a,\sqrt{4+x}=b.\)

\(\Rightarrow\hept{\begin{cases}a+b=3\\a^2+b^2=5\end{cases}\Leftrightarrow\hept{\begin{cases}\left(a+b\right)^2=9\\a^2+b^2=5\end{cases}\Rightarrow}ab=2\Rightarrow\left(a-b\right)^2=1.\Rightarrow\orbr{\begin{cases}a-b=1\\a-b=-1\end{cases}\Rightarrow}\orbr{\begin{cases}a=2,b=1\\a=1,b=2\end{cases}}.}\)

Từ đó suy ra x=-3,x=0

ĐKXĐ: \(x\ge1\)

\(\Leftrightarrow x-\sqrt{x^2-1}+x+\sqrt{x^2-1}+2\sqrt{x^2-\left(x^2-1\right)}=4\)

\(\Leftrightarrow2x+2=4\)

\(\Leftrightarrow x=1\)

Bạn tự xét ĐKXĐ nhé ^^

Ta có : \(\sqrt{3x^2-5x+1}-\sqrt{x^2-2}=\sqrt{3\left(x^2-x-1\right)}-\sqrt{x^2-3x+4}\)

\(\Leftrightarrow\left(\sqrt{3x^2-5x+1}-\sqrt{3}\right)-\left(\sqrt{x^2-2}-\sqrt{2}\right)-\left[\sqrt{3\left(x^2-x-1\right)}-\sqrt{3}\right]+\left(\sqrt{x^2-3x+4}-\sqrt{2}\right)=0\)

\(\Leftrightarrow\frac{3x^2-5x+1-3}{\sqrt{3x^2-5x+1}+\sqrt{3}}-\frac{x^2-2-2}{\sqrt{x^2-2}+\sqrt{2}}-\frac{3x^2-3x-3-3}{\sqrt{3\left(x^2-x-1\right)}+\sqrt{3}}+\frac{x^2-3x+4-2}{\sqrt{x^2-3x+4}+\sqrt{2}}=0\)

\(\Leftrightarrow\frac{\left(x-2\right)\left(3x+1\right)}{\sqrt{3x^2-5x+1}+\sqrt{3}}-\frac{\left(x-2\right)\left(x+2\right)}{\sqrt{x^2-2}+\sqrt{2}}-\frac{3\left(x-2\right)\left(x+1\right)}{\sqrt{3\left(x^2-x-1\right)}+\sqrt{3}}+\frac{\left(x-2\right)\left(x-1\right)}{\sqrt{x^2-3x+4}+\sqrt{2}}=0\)

\(\Leftrightarrow\left(x-2\right)\left(\frac{3x+1}{\sqrt{3x^2-5x+1}+\sqrt{3}}-\frac{x+2}{\sqrt{x^2-2}+\sqrt{2}}-\frac{3x+3}{\sqrt{3\left(x^2-x-1\right)}+\sqrt{3}}+\frac{x-1}{\sqrt{x^2-3x+4}+\sqrt{2}}\right)=0\)Tới đây bạn tự làm tiếp ^^

Dài quá ^^

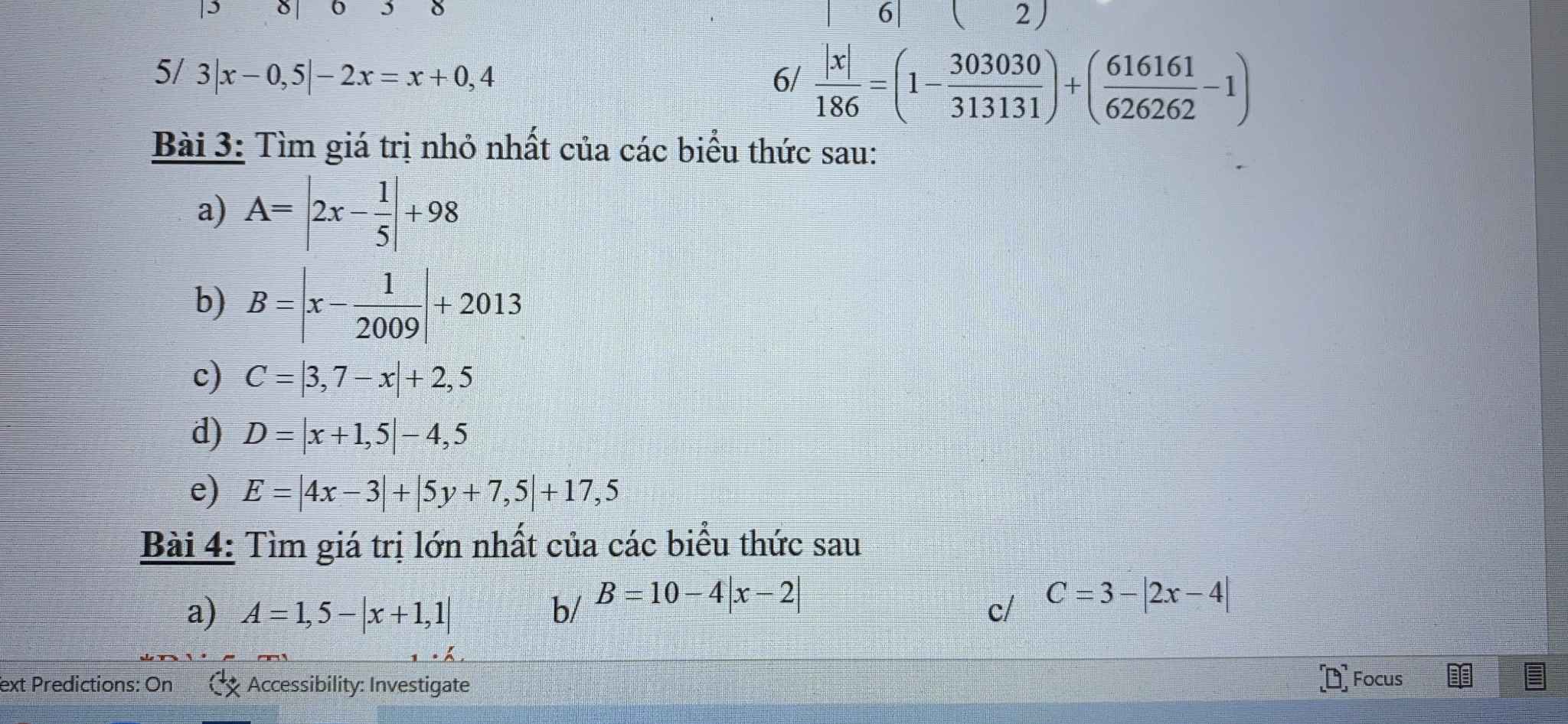
Bài 4:

a: Ta có: \(-\left|x+1.1\right|\le0\forall x\)

\(\Leftrightarrow-\left|x+1.1\right|+1.5\le1.5\forall x\)

Dấu '=' xảy ra khi x=-1,1

b: Ta có: \(-4\left|x-2\right|\le0\forall x\)

\(\Leftrightarrow-4\left|x-2\right|+10\le10\forall x\)

Dấu '=' xảy ra khi x=2

các bn giúp mink nha

Trả lời: 

\(\left(x+1\right)+\left(x+2\right)+\left(x+3\right)+...+\left(x+9\right)+\left(x+10\right)=240\)

\(\Leftrightarrow\left(x+x+x+...+x+x\right)+\left(1+2+3+...+9+10\right)=240\)

\(\Leftrightarrow10x+\left(10+1\right)\times\left[\left(10-1\right)\div1+1\right]\div2=240\)

\(\Leftrightarrow10x+11\times10\div2=240\)

\(\Leftrightarrow10x+55=240\)

\(\Leftrightarrow10x=185\)

\(\Leftrightarrow x=18,5\)

Vậy \(x=18,5\)

( x+1 )+( x+2 )+...+( x+10 ) = 240

= x+1 + x+2 + x+3 +...+ x+9 + x+10 = 240

= ( x+x+x+...+x ) + ( 1+2+3+...+9+10 ) = 240

= 10.x + 55 = 240

   10.x = 240-55

   10.x = 185

     x  = 185 : 10

    x  = 18,5

mn giúp mink 

mn giúp mink nha

=>(-4) x y -5= -9

=>(-4) x y= -4

=> y=1

a, A= \(\frac{\sqrt{x}+1}{\left(\sqrt{x}+2\right)^2}:\left(\frac{\left(\sqrt{x}\right)^2}{\sqrt{x}\left(\sqrt{x}+2\right)}+\frac{x}{\sqrt{x}+2}\right)\)

A=\(\frac{\sqrt{x}+1}{\left(\sqrt{x}+2\right)^2}:\left(\frac{\sqrt{x}}{\left(\sqrt{x}+2\right)}+\frac{x}{\sqrt{x}+2}\right)\)

A=\(\frac{\sqrt{x}+1}{\left(\sqrt{x}+2\right)^2}:\left(\frac{\sqrt{x}+x}{\left(\sqrt{x}+2\right)}\right)\)

A=\(\frac{1}{x+2\sqrt{x}}\)

b, A >= \(\frac{1}{3\sqrt{x}}\)

=> \(\frac{1}{x+2\sqrt{x}}\) >= \(\frac{1}{3\sqrt{x}}\)

=> x <= -1 , x >= 4 (x khác 0)

\(\left\{{}\begin{matrix}2\left(\dfrac{x^3}{y^2}+\dfrac{y^3}{x^2}\right)=\sqrt[4]{8\left(x^4+y^4\right)}+2\sqrt{xy}\left(1\right)\\16x^5-20x^3+5\sqrt{xy}=\sqrt{\dfrac{y+1}{2}}\left(2\right)\end{matrix}\right.\).

ĐKXĐ: \(xy>0;y\ge-\dfrac{1}{2}\).

Nhận thấy nếu x < 0 thì y < 0. Suy ra VT của (1) âm, còn VP của (1) dương (vô lí)

Do đó x > 0 nên y > 0.

Với a, b > 0 ta có bất đẳng thức \(\left(a+b\right)^4\le8\left(a^4+b^4\right)\).

Thật vậy, áp dụng bất đẳng thức Cauchy - Schwarz ta có:

\(\left(a+b\right)^4\le\left[2\left(a^2+b^2\right)\right]^2=4\left(a^2+b^2\right)^2\le8\left(a^4+b^4\right)\).

Dấu "=" xảy ra khi và chỉ khi a = b.

Áp dụng bất đẳng thức trên ta có:

\(\left(\sqrt[4]{8\left(x^4+y^4\right)}+2\sqrt{xy}\right)^4\le8\left[8\left(x^4+y^4\right)+16x^2y^2\right]=64\left(x^2+y^2\right)^2\)

\(\Rightarrow\left(\sqrt[4]{8\left(x^4+y^4\right)}+2\sqrt{xy}\right)^2\le8\left(x^2+y^2\right)\). (3)

Lại có \(4\left(\dfrac{x^3}{y^2}+\dfrac{y^3}{x^2}\right)^2=4\left(\dfrac{x^6}{y^4}+2xy+\dfrac{y^6}{x^4}\right)\). (4) 

Áp dụng bất đẳng thức AM - GM ta có \(\dfrac{x^6}{y^4}+xy+xy+xy+xy\ge5x^2;\dfrac{y^6}{x^4}+xy+xy+xy+xy\ge5y^2;3\left(x^2+y^2\right)\ge6xy\).

Cộng vế với vế của các bđt trên lại rồi tút gọn ta được \(\dfrac{x^6}{y^4}+2xy+\dfrac{y^6}{x^4}\ge2\left(x^2+y^2\right)\). (5)

Từ (3), (4), (5) suy ra \(4\left(\dfrac{x^3}{y^2}+\dfrac{y^3}{x^2}\right)^2\ge\left(\sqrt[4]{8\left(x^4+y^4\right)}+2\sqrt{xy}\right)^2\Rightarrow2\left(\dfrac{x^3}{y^2}+\dfrac{y^3}{x^2}\right)\ge\sqrt[4]{8\left(x^4+y^4\right)}+2\sqrt{xy}\).

Do đó đẳng thức ở (1) xảy ra nên ta phải có x = y.

Thay x = y vào (2) ta được:

\(16x^5-20x^3+5x=\sqrt{\dfrac{x+1}{2}}\). (ĐK: \(x>0\))

PT này có một nghiệm là x = 1 mà sau đó không biết giải ntn :v