Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

\(\frac{A}{1}=\frac{B}{2}=\frac{C}{3}=\frac{D}{4}=\frac{A+B+C+D}{1+2+3+4}=\frac{360^0}{10}=36^0\)

\(\frac{A}{1}=36^0\Rightarrow A=36^0\times1=36^0\)

\(\frac{B}{2}=36^0\Rightarrow B=36^0\times2=72^0\)

\(\frac{C}{3}=36^0\Rightarrow C=36^0\times3=108^0\)

\(\frac{D}{4}=36^0\Rightarrow D=36^0\times4=144^0\)

Vậy \(A=36^0;B=72^0;C=108^0;D=144^0\)

xét tứ giác ABCD, có: góc A + B + C + D=360*

ta có: A/1 = B/2 = C/3 = D/4

xét tc dãy ts = nhau, có:

A+B+C+D/1+2+3+4 = 360/10 = 36

=> A=36

=> B=36.2=72

=> C=36.3=108

=>D=36.4=144

Xét tứ giác ABCD ta có :

^A + ^B + ^C + ^D = 360⁰(định lí tổng các góc trong một tứ giác)

Mà ^A : ^B : ^C : ^D = 1 : 2 : 3 : 4 => \(\frac{\widehat{A}}{1}=\frac{\widehat{B}}{2}=\frac{\widehat{C}}{3}=\frac{\widehat{D}}{4}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có :

\(\frac{\widehat{A}}{1}=\frac{\widehat{B}}{2}=\frac{\widehat{C}}{3}=\frac{\widehat{D}}{4}=\frac{\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}}{1+2+3+4}=\frac{360^0}{10}=36^0\)

Từ đó suy ra ^A = 36⁰ . 1 = 36⁰ , ^B = 36⁰ . 2 = 72⁰ , ^C = 36⁰ . 3 = 108⁰ , ^D = 36⁰ . 4 = 144⁰

Đến đây tự kết luận

Xét tứ giác ABCD có : 

^A + ^B + ^C + ^D = 360⁰ 

^A ; ^B ; ^C ; ^D tỉ lệ với 1 ; 2 ; 3 ; 4

=> ^A/1 = ^B/2 = ^C/3 = ^D/4 và ^A + ^B + ^C + ^D = 360⁰ 

Áp dụng tính chất dãy tỉ số bằng nhau ta có :

^A/1 = ^B/2 = ^C/3 = ^D/4 = ( ^A + ^B + ^C + ^D )/( 1 + 2 + 3 + 4 ) = 360⁰/10 = 36⁰

^A/1 = 36⁰ => ^A = 36⁰

^B/2 = 36⁰ => ^B = 72⁰

^C/3 = 36⁰ => ^C = 108⁰

^D/4 = 36⁰ => ^D = 144⁰

Vậy ...

a) Vì AB//CD, ta có góc ACD = góc BCD = 180 - góc D = 180 - 60 = 120 độ.

Vì AB//CD, ta có góc ACD = góc BAD.

Vậy số đo góc A là 120 độ.

b) Gọi góc BCD là x độ.

Theo giả thiết, góc B phần góc D = 4/5, ta có:

góc B = (4/5) * góc D

= (4/5) * 60

= 48 độ.

Vì AB//CD, ta có góc BCD = góc BAD.

Vậy góc BAD = góc BCD = x độ.

Vì tứ giác ABCD là tứ giác lồi, tổng các góc trong tứ giác ABCD là 360 độ.

Ta có: góc A + góc B + góc C + góc D = 360 độ.

Vì góc D = 60 độ, góc A = 120 độ và góc B = 48 độ, ta có:

120 + 48 + góc C + 60 = 360

góc C = 360 - 120 - 48 - 60 = 132 độ.

Vậy số đo góc B là 48 độ và số đo góc C là 132 độ.

* Ib = bài 4

1: Đặt góc A=a; góc B=b; góc C=c; góc D=d

Theo đề, ta có: a/1=b/2=c/3=d/4 và a+b+c+d=360

Áp dụng tính chất của DTSBN, ta được:

a/1=b/2=c/3=d/4=(a+b+c+d)/(1+2+3+4)=360/10=36

=>a=36; b=72; c=108; d=144

2:

góc C+góc D=360-130-105=230-105=125

góc C-góc D=25 độ

=>góc C=(125+25)/2=75 độ và góc D=75-25=50 độ

3:

góc B=360-57-110-75=118 độ

số đo góc ngoài tại B là:

180-118=62 độ

bài 5; tính số đo các góc của tứ giác ABCD biết góc A = 60 độ; góc B = 90 độ. Tính số đo của góc C và góc D:

a, góc C = 100 độ; góc D = 60 độ;

góc A 

C, góc B = 80 độ; góc C = 60 độ; 5 góc A = 6 góc D

ý A nha

a) Ta có: AB = AD (gt)  => A thuộc đường trung trực của BD

CB = CD (gt)   => C thuộc đường trung trực của BD.

Vậy AC là đường trung trực của BD.

b) Xét ∆ ABC và ∆ADC có AB = AD (gt)

nên ∆ ABC = ∆ADC (c.c.c)

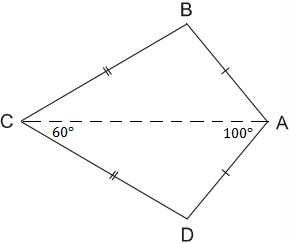
Suy ra: ⇒ˆB=ˆD

Ta có ˆB+ˆD=360⁰–(100+60)=20⁰

 Do đó ˆB=ˆD=100⁰

mban trl giúp mình câu C luôn nha ạ😭

Mình làm hơi tắt

Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)

    Mà \(\widehat{A}=2\times\widehat{C}\left(gt\right)\)

          \(\widehat{B}=\widehat{D}=117^o\)theo câu b)

\(\Rightarrow2\times\widehat{C}+117^o+\widehat{C}+117^o=360^o\)

\(\Rightarrow3\times\widehat{C}=360^o-117^o-117^o=126^o\)

\(\Rightarrow\widehat{C}=\frac{126^o}{3}=42^o\)

\(\Rightarrow\widehat{A}=2\times\widehat{C}=2\times42^o=84^o\)

Vậy \(\widehat{A}=84^o;\widehat{B}=117^o;\widehat{C}=42^o;\widehat{D}=117^o\)