Cho tam giác ABC, vuông ở A. Trên cạnh AB lấy điểm D, trên cạnh BC lấy điểm E sao cho DE vuông góc với BC. AE cắt CD tại K. Chứng minh rằng:
a) BE . BC = BD . BA
b) KD . KC = KA . KE
Những câu hỏi liên quan
Cho Tam giác ABC cân tại A .Từ A vẽ AK vuông góc với BC (K thuộc BC) a) Chứng minh tam giác AKB = tam giác AKC b) Trên canh AB lấy điểm D ,trên cạnh CA lấy điểm E sao cho AE =AD .Chứng minh KE=KD ,c) Chứng minh ED //BC,D) trên tia đối của tia CA lấy điểm H sao cho CE =CH .Đườngthẳng HD cắt BC Tại L .Chứng minh IH=ID
Xem chi tiết
Cho Tam giác ABC cân tại A .Từ A vẽ AK vuông góc với BC (K thuộc BC)
a) Chứng minh tam giác AKB = tam giác AKC
b) Trên canh AB lấy điểm D ,trên cạnh CA lấy điểm E sao cho AE =AD .Chứng minh KE=KD ,
c) Chứng minh ED //BC,
D) trên tia đối của tia CA lấy điểm H sao cho CE =CH .Đườngthẳng HD cắt BC Tại L .Chứng minh IH=ID
Xem chi tiết
1. Cho ∆ABC vuông tại A (AB AC). Vẽ tia BD là phân giác của góc ABC (D ∈ AC). Trên cạnh BC lấy điểm E sao cho BA BE.a. Chứng minh: ∆BAD ∆BEDb. Từ A kẻ AH ⊥ BC tại H. Chứng minh: AH // DEc. Trên tia đối của tia ED lấy điểm K sao cho ED EK. Chứng minh: Góc EKC góc ABC2.Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BE BA. Phân giác góc B cắt AC tại D. a. Chứng minh ∆ABD Đồng ý∆EBD và DE ⊥ BCb. Gọi K là giao điểm của tia ED và tia BA. Chứng minh AK EC.c. Gọi M là trung điểm c...
Đọc tiếp
1. Cho ∆ABC vuông tại A (AB < AC). Vẽ tia BD là phân giác của góc ABC (D ∈ AC). Trên cạnh BC lấy điểm E sao cho BA = BE.
a. Chứng minh: ∆BAD = ∆BED
b. Từ A kẻ AH ⊥ BC tại H. Chứng minh: AH // DE
c. Trên tia đối của tia ED lấy điểm K sao cho ED = EK. Chứng minh: Góc EKC = góc ABC
2.
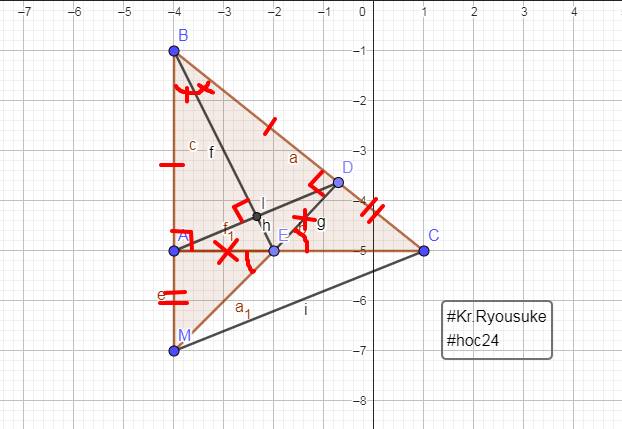
Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BE = BA. Phân giác góc B cắt AC tại D.
a. Chứng minh ∆ABD = Đồng ý∆EBD và DE ⊥ BC
b. Gọi K là giao điểm của tia ED và tia BA. Chứng minh AK = EC.
c. Gọi M là trung điểm của KC. Chứng minh ba điểm B, D, M thẳng hàng.
3.
Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm M sao cho BA = BM. Gọi E là trung điểm AM.
a.Chứng minh: ∆ABE = ∆MBE.
b. Gọi K là giao điểm BE và AC. Chứng minh: KM ⊥ BC,
c. Qua M vẽ đường thẳng song song với AC cắt BK tại F. Trên đoạn thẳng KC lấy điểm Q sao cho KQ = MF. Chứng minh: góc ABK = QMC
4
Cho tam giác ABC có AB = AC, lấy M là trung điểm của BC.
a) Chứng minh ∆ABM = ∆ACM
b) Kẻ ME ⊥ AB tại Em kẻ MF ⊥ AC tại F. Chứng minh AE = AF.
c) Gọi K là trung điểm của EF. Chứng minh ba điểm A, K, M thẳng hàng
d) Từ C kẻ đương thẳng song song với AM cắt tia BA tại D. Chứng minh A là trung điểm của BD.
4:
a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
b: Xet ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF
c: AE=AF
ME=MF
=>AM là trung trực của EF
mà K nằm trên trung trực của EF
nên A,M,K thẳng hàng
Đúng 0
Bình luận (0)
4:
a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
b: Xet ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF
=>AM là trung trực của EF
mà K nằm trên trung trực của EF
nên A,M,K thẳng hàng
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC có CA CB 10 cm AB 12 cm. Kẻ CI vuông góc với AB (I thuộc AB )a,chứng minh rằng IAIBb, Tính độ dài ICc, Kẻ IH vuông với AC (H thuộc AC) kẻ IK vuông góc với BC (K thuộc BC).So sánh các độ dài IH và IKBài 2: cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm D. Trên cạnh AC lấy điểm E sao cho ADAEa, chứng minh rằng BECDb, chứng minh rằng góc ABE bằng góc ACDc, Gọi K là giao điểm của BE và CD. Tam giác KBC là tam giác gì? Vì sao?Bài 3: Cho tam giác ABC vuông ở C, có góc A b...
Đọc tiếp
Bài 1: Cho tam giác ABC có CA = CB = 10 cm AB = 12 cm. Kẻ CI vuông góc với AB (I thuộc AB )
a,chứng minh rằng IA=IB
b, Tính độ dài IC
c, Kẻ IH vuông với AC (H thuộc AC) kẻ IK vuông góc với BC (K thuộc BC).So sánh các độ dài IH và IK
Bài 2: cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm D. Trên cạnh AC lấy điểm E sao cho AD=AE
a, chứng minh rằng BE=CD
b, chứng minh rằng góc ABE bằng góc ACD
c, Gọi K là giao điểm của BE và CD. Tam giác KBC là tam giác gì? Vì sao?
Bài 3: Cho tam giác ABC vuông ở C, có góc A bằng 60 độ tia phân giác của góc BAC cắt BC ở E kẻ CK vuông góc với AB (K thuộc AB) kẻ BD vuông góc với tia AE (D thuộc tia AE)chứng minh:
a, AC=AK và AE vuông góc CK
b,KB=KA
c, EB > AC
d, ba đường AC,BD,KE cùng đi qua 1 điểm
Bài 4: Cho tam giác nhọn ABC vẽ ra phía ngoài tam giác ABC các tam giác đều ABD và ACE .Gọi M là giao điểm của DC và BE Chứng minh rằng:
a, tam giác ABE=tam giác ADC
b,góc BMC=120°
Bài 5: Cho tam giác ABC vuông ở C ,có góc A bằng 60 độ tia phân giác của góc BAC cắt BC ở E,kẻ EK vuông góc với AB( K thuộc AB)kẻ BD vuông góc với AE (D thuộc AE) chứng minh
a,AK=KB
b, AD=BC
C1 :
Hình : tự vẽ
a )Vì CA=CB ( đề bài cho ) => tam giác ABC cân tại C
mà CI vuông góc vs AB => CI là đường cao của tam giác ABC
=> CI cũng là đường trung tuyến của tam giác ABC ( t/c tam giác cân )
=> IA=IB (đpcm)
Đúng 0
Bình luận (0)
C1 :
b) Có IA=IB ( cm phần a )
mà IA+IB = AB
IA + IA = 12 (cm)
=> IA = \(\frac{12}{2}=6\left(cm\right)\)
Xét tam giác vuông CIA có : CI2 + IA2 = CA2 ( Đ/l Py-ta -go )
CI2 + 62 = 102
CI2 = 102 - 62 = 64
=> CI = \(\sqrt{64}=8\left(cm\right)\)
Vậy CI ( hay IC ) = 8cm
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A ( AB < AC ) . Trên cạnh BC lấy điểm D sao cho BD = BA . Đường vuông góc với BC tại D cắt AC ở E
a , Chứng minh AE = DE
b , Giả sư AB/3 = AC/4 , BC = 10 cm .Tính độ dài BD
c , Đường phân giác góc ngoài tại đỉnh C cắt đường BE ở K . Tính số đo góc BAK
1)Cho tam giác ABC vuông cân tại A trên AB lấy D trên AC lấy E sao cho AD=AE qua D và A kẻ các đường thẳng vuông góc BE cắt BC tại I và K chứng minh IK=KC
2) cho tam giác ABC vuông tại A vẽ tam giác vuông cân DAB có cạnh huyền AB, E là trung điểm BC tính DE
Cho ABC vuông tại A có AB AC, Trên cạnh BC lấy điểm D sao cho BA BD. Từ D kẻ DE BC (E AC), Đường thẳng DE cắt đường thẳng AB tại M. Chứng minh rằng a) Tam giác ABE Tam giác DBE b) BE Vuông Góc AD c) Tam giác MBC cân
Đọc tiếp
Cho ABC vuông tại A có AB < AC, Trên cạnh BC lấy điểm D sao cho BA = BD. Từ D kẻ DE BC (E AC), Đường thẳng DE cắt đường thẳng AB tại M. Chứng minh rằng
a) Tam giác ABE = Tam giác DBE
b) BE Vuông Góc AD
c) Tam giác MBC cân
a: Xét ΔBAE vuông tại A và ΔBDE vuông tại D co
BE chung
BA=BD
=>ΔBAE=ΔBDE
b: BA=BD
EA=ED
=>BE là trung trực của AD
c: Xét ΔBDM vuông tại D và ΔBAC vuông tại A có
BD=BA
góc B chung
=>ΔBDM=ΔBAC
=>BM=BC
=>ΔBMC cân tại B
Đúng 1
Bình luận (1)
`a,`
Xét `2 \Delta` vuông `ABE` và `DBE`:
`\text {BE chung}`
`\text {BA = BD (2 cạnh tương ứng)}`
`=> \Delta ABE = \Delta DBE (ch-cgv)`
`b,`
Gọi I là giao điểm của AD và BE
Vì `\Delta ABE = \Delta DBE (a)`
`->` $\widehat {ABE} = \widehat {DBE} (\text {2 góc tương ứng})$
Xét `\Delta ABI` và `\Delta DBI`:
`\text {BA = BD (gt)}`
$\widehat {ABI} = \widehat {DBI}$
`\text {BI chung}`
`=> \Delta ABI = \Delta DBI (c-g-c)`
`->` $\widehat {BIA} = \widehat {BID} (\text {2 cạnh tương ứng})$
Mà `2` góc này ở vị trí kề bù
`->` $\widehat {BIA} + \widehat {BID} = 180^0$
`->` $\widehat {BIA} = \widehat {BID} =$\(\dfrac{180}{2}=90^0\)
`-> \text {BI} \bot \text {AD}`
Mà `\text {I} \in \text {BE}`
`-> \text {BE} \bot \text{AD}`
`c,`
Vì `\Delta ABE = \Delta DBE (a)`
`-> \text {AE = DE (2 cạnh tương ứng)}`
Xét `\Delta AEM` và `\Delta DEC`:
`\text {AE = DE}`
$\widehat {AEM} = \widehat {DEC} (\text {2 góc đối đỉnh})$
$\widehat {MAE} = \widehat {CDE} (=90^0)$
`=> \Delta AEM = \Delta DEC (cgv-gn)`
`-> \text {AM = DC (2 cạnh tương ứng)}`
Ta có: \(\left\{{}\begin{matrix}\text{BM = AM + AB}\\\text{BC = BD + DC}\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}\text{BA = BD}\\\text{AM = DC}\end{matrix}\right.\)
`-> \text {BM = BC}`
Xét `\Delta MBC`:
`\text {BM = BC}`
`-> \Delta MBC` cân tại B.
Đúng 0
Bình luận (0)
1. Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm D. Trên cạnh AC lấy E sao cho ADAE.a, CmBECDb,Cm góc ABE góc ACDc, Gọi K là giao điểm của BE và CD. Tam giác KBC là tam giác gì? vì sao?2.Cho tam giác ABC vuông ở C, có góc A60 độ. Tia phân giác của góc BAC cắt BC ở E. Kẻ EK vuông góc với AB(K thuộc AB). Kẻ BD vuông góc với tia AE(D thuộc tia AE). Cm:a, ACAK và AE vuông góc CKb, KBKAc,EBACd,Ba đường thẳng AC,BD,KE cùng đi qua một điểm.
Đọc tiếp
1. Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm D. Trên cạnh AC lấy E sao cho AD=AE.
a, CmBE=CD
b,Cm góc ABE = góc ACD
c, Gọi K là giao điểm của BE và CD. Tam giác KBC là tam giác gì? vì sao?
2.Cho tam giác ABC vuông ở C, có góc A=60 độ. Tia phân giác của góc BAC cắt BC ở E. Kẻ EK vuông góc với AB(K thuộc AB). Kẻ BD vuông góc với tia AE(D thuộc tia AE). Cm:
a, AC=AK và AE vuông góc CK
b, KB=KA
c,EB>AC
d,Ba đường thẳng AC,BD,KE cùng đi qua một điểm.
1,a, cm: tam giác BEC và tg BDC(c.g.c0
b, cm : tg ABE= tg ACD(c,g.c)
c, cm: BK=KC ( cm: tg BKD= tg CED)
Đúng 0
Bình luận (0)
CHO tam giác ABC có A =90 ,AB=8CM,AC=6CM
a, Tính BC
b, Trên cạnh AC lấy điểm E sao cho AE=2CM,, Trên tia đối của tia AB lấy điểm D sao cho AD=AB.chứng minh tam giác BEC=DEC
c, Chuwsngh minh DE ĐI QUA trung điểm cạnh BC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại A. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD=AE. Gọi K là điểm bất kì trên BC, trên nửa mặt phẳng bờ AC không chứa B lấy điểm I sao cho AI=AK và góc DAK=góc EAI. Chứng minh rằng KD+KE>=AB.