Cho hình thang cân có AB//CD, AB=17cm, CD=33cm và BD là tia phân giác góc D
a) Tính độ dài cạnh BC và chu vi hình thang ABCD
b) Trên đấy CD Lấy điểm E sao cho DE=AB. Tam giác BEC là tam giác gì

Những câu hỏi liên quan
Cho hình thang cân có AB//CD, AB=17cm, CD=33cm và BD là tia phân giác góc D
a) Tính độ dài cạnh BC và chu vi hình thang ABCD
b) Trên đấy CD Lấy điểm E sao cho DE=AB. Tam giác BEC là tam giác gì
2/ Cho hình thang cân ABCD ( Ab song song Cd) có AB=17cm và Cd = 33cm và DB là tia phân giác cuả góc D . a/Hãy tính độ dài cạnh BC và chu vi hình thang b/trên đáy CD lấy Esao cho De=AB . Tam giác BEC là tam giác gì
Bài 1: Cho tam giác ABC .Trên tia AC lấy điểm M sao cho AM AB. Trên tia AB lấy điểm N sao cho AN AC. Chứng minh tứ giác BMCN là hình thangBài 2: Cho tam giác ABC vuông tại A. Lấy điểm M thuộc cạnh BC sao cho AM 1/2 BC, N là trung điểm cạnh AB. Chứng minh:a) Tam giác ABC cân ---- b) Tứ giác MNAC là hình thang vuông Bài 3: Cho hình thang cân ABCD ( AB // CD ) ---- a) Chứng minh góc ACD góc BCD ---- b) Gọi E là giao điểm của AC và BD. C/minh EA EBBài 4: Cho ABCD là hình thang ( AB // CD, AB CD...
Đọc tiếp
Bài 1: Cho tam giác ABC .Trên tia AC lấy điểm M sao cho AM = AB. Trên tia AB lấy điểm N sao cho AN = AC. Chứng minh tứ giác BMCN là hình thang
Bài 2: Cho tam giác ABC vuông tại A. Lấy điểm M thuộc cạnh BC sao cho AM= 1/2 BC, N là trung điểm cạnh AB. Chứng minh:
a) Tam giác ABC cân ---- b) Tứ giác MNAC là hình thang vuông
Bài 3: Cho hình thang cân ABCD ( AB // CD ) ---- a) Chứng minh góc ACD = góc BCD ---- b) Gọi E là giao điểm của AC và BD. C/minh EA = EB
Bài 4: Cho ABCD là hình thang ( AB // CD, AB < CD ). Kẻ các đường cao AE,BF của hình thang. C/minh rằng DE = CF
Bài 5: Cho ABCD là hình thang ( AB // CD ) có DB là đường phân giác góc D và AE là đường phân giác góc A ( E thuộc DC ). Biết AE // BC và O là giao điểm của AE với DB. CMR:
a) AE vuông góc với DB
b) AD // BE và AD = BE
c) E là trung điểm của DC
d) Xác định dạng của tứ giác BCEO
e) Biết góc BEC = 80 độ. Hãy tính các góc của hình thang ABCD
Bài 4:
Xét ΔAED vuông tại E và ΔBFC vuông tại F có
AD=BC
góc D=góc C
Do đó: ΔAED=ΔBFC
=>DE=CF
Bài 3:
a: Xét ΔADC và ΔBCD có
AD=BC
AC=BD
DC chung
Do đó: ΔADC=ΔBCD
=>góc ACD=góc BDC
b: Ta co: góc ACD=góc BDC
=>góc EAB=góc EBA
=>ΔEAB cân tại E
Đúng 0
Bình luận (0)
1. chứng minh răng hình thang có hai đường chéo bằng nhay là hình thang cân.2. cho hình thang ABCD (AB//CD), biết góc B- góc C 240 và góc A 1.5 góc D. Tính các góc của hình thang3. Cho hình thang ABCD (AB//CD). các tia phân giác của góc A và góc B cắt nhau tại điểm E trên cạnh đáy CD. Chứng minh rằng CDAD+BC.4. Cho tam giác ABC vuông cân ở A. Trên nửa mặt phẳng bờ BC không chứa đỉnh A, vẽ BD vuông với BC và BDBC.a) tính các góc của hình thangb) biết AB5 cm. tính CD5.Cho hình thang vuông ABCD có...
Đọc tiếp
1. chứng minh răng hình thang có hai đường chéo bằng nhay là hình thang cân.
2. cho hình thang ABCD (AB//CD), biết góc B- góc C= 240 và góc A= 1.5 góc D. Tính các góc của hình thang
3. Cho hình thang ABCD (AB//CD). các tia phân giác của góc A và góc B cắt nhau tại điểm E trên cạnh đáy CD. Chứng minh rằng CD=AD+BC.
4. Cho tam giác ABC vuông cân ở A. Trên nửa mặt phẳng bờ BC không chứa đỉnh A, vẽ BD vuông với BC và BD=BC.
a) tính các góc của hình thang
b) biết AB=5 cm. tính CD
5.Cho hình thang vuông ABCD có góc A= góc D = 900, đường chéo BD vuông góc với cạnh bên BC và BD=BC.
a) tính các góc của hình thang
b) biết AB=3cm. tính độ dài các cạnh BC,CD.
6. Hình thang cân ABCD có AB//CD, AB<CD. Kẻ hai đường cao AH, BK.
a) chứng minh ằng HD=KC.
7. Cho tam giác cân ABC (AB=AC), phân giác BD,CE.
a) tú giác BEDC là hình gì?Vì sao?
b)Chứng minh BE=ED=DC.
c) biết góc A=500. Tính các góc của tứ giác BEDC.
8. cho tam giác đều ABC, hai đường cao BN,CM
a) chứng minh tứ giác BMNC là hình thang cân
b) Tính chu vi của hình thang BMNC là hình thang cân
làm đc câu ào thì đc đâu nhất thiết phải làm hết chỉ là mik đưa mấy bài đóa để mấy bn chỉ đc bài nào thì chỉ thôi mà
Đúng 0
Bình luận (0)
cho hình thang ABCD(ABsong song CD)Có AC vuông gócBD,AB=5cm, CD=12cm.Tính chiều caoBH
Đúng 0
Bình luận (0)
Cho hình thang cân ABCD (AB // CD) có AB = 17cm, CD = 33cm và DB là tia phân giác của góc D.
a) Hãy tính độ dài cạnh BC và chu vi hình thang ABCD.
b) Trên đáy CD lấy điểm E sao cho DE = AB. Tam giác BEC là tam giác gì
a: góc ABD=góc BDC
=>góc ABD=góc ADB
=>ΔABD cân tại A
=>AB=AD=17cm
=>BC=17cm
b: Xét tứ giác ABED có
AB//ED
AB=ED
AB=ED
=>ABED là hình thoi
=>góc BEC=góc ADE
=>góc BEC=góc BCE
=>ΔBCE cân tại B
Đúng 0
Bình luận (0)
Bài 1: Cho hình thang cân ABCD có AB//CD, đường chéo DB vuông góc với cạnh bên BC, DB là tia phân giác góc D. Tính chu vi của hình thang, biết BC3cm.
Bài 2: Cho tam giác ABC cân tại A, các đường phân giác BD,CE (D thuộc AC, E thuộc AB)
a) Chứng minh BEDC là hình thang cân
b) Tính các góc của hình thang cân BEDC, biết góc C50 độ
Bài 3: Cho hình thang cân ABCD có AB//CD, O là giao điểm của hai đường chéo, E là giao điểm của hai đường thẳng chứa cạnh bên AD v...
Đọc tiếp
Bài 1: Cho hình thang cân ABCD có AB//CD, đường chéo DB vuông góc với cạnh bên BC, DB là tia phân giác góc D. Tính chu vi của hình thang, biết BC=3cm.
Bài 2: Cho tam giác ABC cân tại A, các đường phân giác BD,CE (D thuộc AC, E thuộc AB)
a) Chứng minh BEDC là hình thang cân
b) Tính các góc của hình thang cân BEDC, biết góc C=50 độ
Bài 3: Cho hình thang cân ABCD có AB//CD, O là giao điểm của hai đường chéo, E là giao điểm của hai đường thẳng chứa cạnh bên AD và BC. Chứng minh:
a) OA=OB , OC=OD
b) EO là đường trung trực của hai đáy hình thang ABCD.
Các bạn giải giúp mình bài này nhé. Cảm ơn các bạn.
Bài 1: Cho hình thang cân ABCD có AB//CD, đường chéo DB vuông góc với cạnh bên BC, DB là tia phân giác góc D. Tính chu vi của hình thang, biết BC3cm.
Bài 2: Cho tam giác ABC cân tại A, các đường phân giác BD,CE (D thuộc AC, E thuộc AB)
a) Chứng minh BEDC là hình thang cân
b) Tính các góc của hình thang cân BEDC, biết góc C50 độ
Bài 3: Cho hình thang cân ABCD có AB//CD, O là giao điểm của hai đường chéo, E là giao điểm của hai đường thẳng chứa cạnh bên AD v...
Đọc tiếp
Bài 1: Cho hình thang cân ABCD có AB//CD, đường chéo DB vuông góc với cạnh bên BC, DB là tia phân giác góc D. Tính chu vi của hình thang, biết BC=3cm.
Bài 2: Cho tam giác ABC cân tại A, các đường phân giác BD,CE (D thuộc AC, E thuộc AB)
a) Chứng minh BEDC là hình thang cân
b) Tính các góc của hình thang cân BEDC, biết góc C=50 độ
Bài 3: Cho hình thang cân ABCD có AB//CD, O là giao điểm của hai đường chéo, E là giao điểm của hai đường thẳng chứa cạnh bên AD và BC. Chứng minh:
a) OA=OB , OC=OD
b) EO là đường trung trực của hai đáy hình thang ABCD.
Các bạn giải giúp mình bài này nhé. Cảm ơn các bạn.
Bài 2:
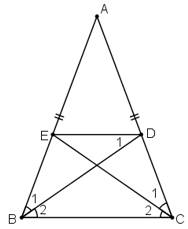
Ta có: ∆ABC là ∆ cân tại A(gt)
=>∠ABC=∠ACB
+Ta có BD là tia pgiac của ∠ABC
=>∠B1=∠B2=1/2∠ABC
+Ta có CE là tia pgiac ∠ACB
=>C1=C2=1/2∠ACB
Xét ∆
AEC và ΔADB có:
+∠A chung
+AB=AC
+C1=B1
=> ΔAEC = ΔADB
=> AE = AD
=>BCDE là hình thang cân
b) Ta có ∠ACB=∠ABC=50o(do BCDE là hình thang cân)
Ta có: ED//BC
\(\Rightarrow\left\{{}\begin{matrix}\widehat{ABC}=\widehat{AED}\\\widehat{ACB}=\widehat{ADE}\end{matrix}\right.=50^o}\) (SLT)
Mà ∠DEB=∠EDC
Ta có:
+∠DEB+∠AED=180o (kề bù)
=>50o+∠AED=180o
=>∠AED=180o-50o=130o
=>∠AED=∠ADE=130o
Đúng 1
Bình luận (0)
Bài 1:
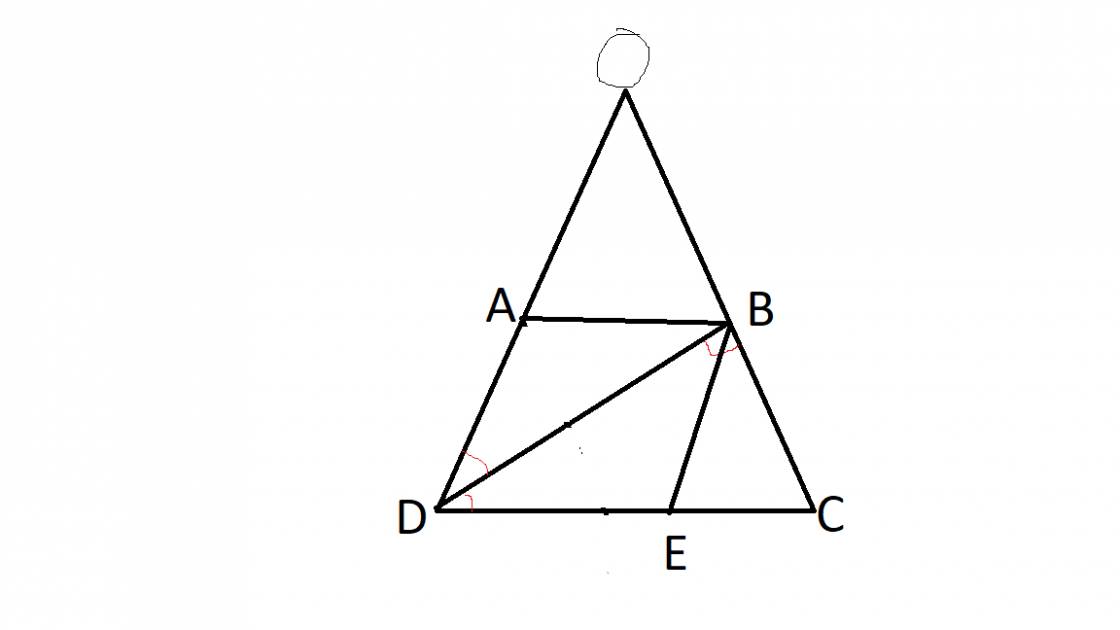
Ta có: AD=BC=3cm (t/c hthang)
Vì AB//CD(gt) nên \(\widehat{ABD}=\widehat{BDC}\left(SLT\right)\)
Mà \(\widehat{ADC}=\widehat{BDC}\) (do BD là tia pgiac góc D)
=>∠ABD=∠BDC
=>∆ABD cân tại A
=>AD=BC=3cm
Vì ∆DBC vuông tại B
nên ∠BDC+∠C=90o
Mà ∠ADC=∠C (do ABCD là hình thang cân)
và ∠BDC=1/2 ∠ADC
=> ∠BCD=1/2∠C
Khi đó: ∠C+1/2∠C=90o=>∠C=60o
- Kẻ từ B 1 đường thẳng // AD cắt CD tại E
Hình thang ABED có hai cạnh bên song song nên AB = DE và AD = BE
⇒ DE = 3 (cm), BE = 3 (cm)
Mà ∠BEC=∠ADC(đồng vị)
=>∠BEC=∠C
=>∆BEC cân tại B có ∠C=60o
=>∆BEC là ∆ cả cân cả đều
=> EC=BC=3cm
Ta có: CD = CE + ED = 3 + 3 = 6(cm)
Chu vi hình thang ABCD bằng:
AB + BC + CD + DA = 3 + 3 + 6 + 3 = 15 (cm)
Đúng 1
Bình luận (0)
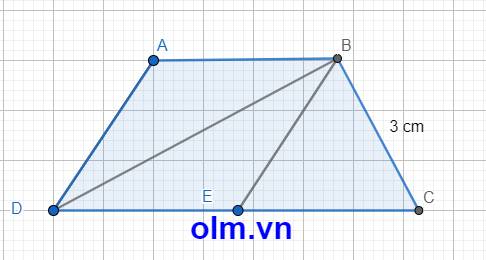
Xét \(\Delta\)ABD có: \(\widehat{ABD}\) = \(\widehat{BDC}\) ( hai góc so le trong)
\(\widehat{ADB}\) = \(\widehat{BDC}\) (BD là phân giác của góc \(\widehat{ABD}\))
⇒ \(\widehat{ABD}\) = \(\widehat{ADB}\) (vì cùng bằng góc BDC)
⇒ \(\Delta\) ABD cân tại A ⇒ AB = AD = 3 cm
Gọi E là trung điểm của DC ta có:\(\Delta\)BCD vuông tại B nên
BE = DE = EC (trong tam giác vuông trung tuyến ứng với cạnh huyền bằng \(\dfrac{1}{2}\) cạnh huyền)
Mặt khác ta có: \(\widehat{ADC}\) = \(\widehat{DCB}\) ( vì ABCD là hình thang cân)
⇒\(\widehat{BDC}\) = \(\dfrac{1}{2}\) \(\widehat{DCB}\) ⇒ \(\widehat{DCB}\) + \(\dfrac{1}{2}\)\(\widehat{DCB}\) = 900
⇒ \(\widehat{DCB}\) \(\times\) ( 1 + \(\dfrac{1}{2}\)) = 900
⇒ \(\widehat{DCB}\) = 900 : \(\dfrac{3}{2}\) = 600
Xét \(\Delta\)BCE có BE = EC và \(\widehat{BCE}\) = 600 nên \(\Delta\)BCE là tam giác đều
⇒ BE = EC = BC = 3 cm
⇒ DC = BE \(\times\) 2 = 3 \(\times\) 2 = 6 cm
Chu vi của hình thang ABCD là:
3 + 3 + 6 + 3 = 15 (cm)
Kết luận chu vi hình thang là: 15 cm
Đúng 1
Bình luận (0)
Cho hình thang ABCD(AB//CD) có ^D=60 ddoooj và CD=3AB=3AD
M,N lần lượt là trung điểm của AB, CD trên cạnh CD lấy E sao cho DE=1/3CD
a) Tứ giác ABED là hình gì
b)CMR MBNE là hình chữ nhật
c) biết AB=a tính chu vi tam giác DBC
B1, Cho tứ giác ABCD có các tia p/giác của góc A và góc D vuông góc với nhau.Chứng minh:a)ABCD là hình thangb) Hai tia phân giác của góc C và D vuông góc với nhauB2, Cho hình thang ABCD có đáy AB40,CD80, cạnh bên BC50,AD30. Chứng minh ABCD là hình thang vuôngB3.Cho tam giác MNP vuông cân ở M, đường thẳng d bất kỳ qua M ( d không cắt NP). Trên d lấy A,B sao cho MAPB vàMBNA. Tứ giác ANPB là hình gì?B4. Cho ABCD là hình thang có BD là phân giác góc D và AE là p/giác góc A ( E nằm trên CD). Biết AE...
Đọc tiếp
B1, Cho tứ giác ABCD có các tia p/giác của góc A và góc D vuông góc với nhau.Chứng minh:
a)ABCD là hình thang
b) Hai tia phân giác của góc C và D vuông góc với nhau
B2, Cho hình thang ABCD có đáy AB=40,CD=80, cạnh bên BC=50,AD=30. Chứng minh ABCD là hình thang vuông
B3.Cho tam giác MNP vuông cân ở M, đường thẳng d bất kỳ qua M ( d không cắt NP). Trên d lấy A,B sao cho MA=PB vàMB=NA. Tứ giác ANPB là hình gì?
B4. Cho ABCD là hình thang có BD là phân giác góc D và AE là p/giác góc A ( E nằm trên CD). Biết AE//BC và Olà giao điểm của AE và DB. Chứng minh:
a) AE vuông góc BD
b) AD//BE và AD=BE
c) E là trung điểm DC
d) Tứ giác BCEO là hình gì?
e) Biết góc BEC=180 độ. Tính các góc ABCD
Mong mọi người giúp với a.! Mình cảm ơn nhiềuuuuuuuuuuuuuu... lắm! :)















