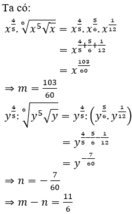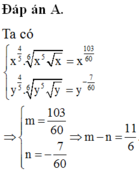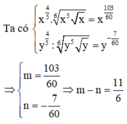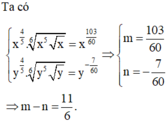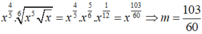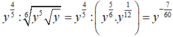Tìm nhân tử chung cho biểu thức sau : xm + xm+8 +x
m+xm+8+x
Đọc tiếp
Tìm nhân tử chung cho biểu thức sau : xm + xm+8 +x
m+xm+8+x
Những câu hỏi liên quan
Cho x 0; y 0. Viết biểu thức
x
4
5
x
5
x
6
về dạng
x
m
và biểu thức
y
4
5
:
y
5
y...
Đọc tiếp
Cho x > 0; y > 0. Viết biểu thức x 4 5 x 5 x 6 về dạng x m và biểu thức y 4 5 : y 5 y 6 về dạng y n . Ta có x m
A. - 11 6
B. 11 6
C. 8 5
D. - 8 5
Tìm các số tự nhiên x thỏa mãn:a) 6 ⋮ (x – 1); b) (x + 11) ⋮ (x + 1). b) 24Mx ; 36Mx ; 160Mx và x lớn nhất.c) 64Mx ; 48Mx ; 88Mx và x lớn nhất. d) xM 4; x M7; xM 8 và x nhỏ nhất khác 0e) x M60 ; x M 45 ; x M 16 0 x 2000 f) x ⋮ 4; x ⋮ 6 và 0 x 50;g) x ⋮ 12; x ⋮ 18 và x ≤ 144;
Đọc tiếp
Tìm các số tự nhiên x thỏa mãn:
a) 6 ⋮ (x – 1); b) (x + 11) ⋮ (x + 1). b) 24Mx ; 36Mx ; 160Mx và x lớn nhất.
c) 64Mx ; 48Mx ; 88Mx và x lớn nhất. d) xM 4; x M7; xM 8 và x nhỏ nhất khác 0
e) x M60 ; x M 45 ; x M 16 0 < x < 2000 f) x ⋮ 4; x ⋮ 6 và 0 < x < 50;
g) x ⋮ 12; x ⋮ 18 và x ≤ 144;
a: \(\Leftrightarrow x-1\in\left\{-1;1;2;3;6\right\}\)
hay \(x\in\left\{0;2;3;4;7\right\}\)
b: \(\Leftrightarrow x+1\in\left\{1;2;5;10\right\}\)
hay \(x\in\left\{0;1;4;9\right\}\)
c: x=UCLN(64;48;88)=8
g: \(x\in BC\left(12;18\right)\)
mà x<=144
nên \(x\in\left\{0;36;72;108;144\right\}\)
Đúng 0
Bình luận (0)
Cho
x
0
,
y
0
. Viết biểu thức
x
4
5
.
x
5
x
6
về dạng
x
m
và biểu thức
y
4...
Đọc tiếp
Cho x > 0 , y > 0 . Viết biểu thức x 4 5 . x 5 x 6 về dạng x m và biểu thức y 4 5 . y 5 y 6 về dạng y = y n . Ta có m - n = ?
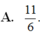
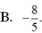
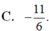
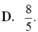
Cho x 0, y 0. Viết biểu thức
x
4
5
.
x
5
x
6
về dạng
x
m
và biểu thức
y
4
5
.
y
5
y
6
về...
Đọc tiếp
Cho x > 0, y > 0. Viết biểu thức x 4 5 . x 5 x 6 về dạng x m và biểu thức y 4 5 . y 5 y 6 về dạng y m . Ta có m - n = ?
A. 11 6
B. - 8 5
C. - 11 6
D. 8 5
Cho
x
0
,
y
0.
Viết biểu thức
x
4
5
.
x
5
x
6
về dạng
x
m
và biểu thức
y
4
5
.
y...
Đọc tiếp
Cho x > 0 , y > 0. Viết biểu thức x 4 5 . x 5 x 6 về dạng x m và biểu thức y 4 5 . y 5 y 6 về dạng y = y n . Ta có m - n = ?
A. 11 6 .
B. − 8 5 .
C. − 11 6 .
D. 8 5 .
Cho x 0 và y 0. Viết biểu thức
x
4
5
.
x
5
x
6
; về dạng
x
m
và biểu thức
y
4
5
.
y
5
y
6...
Đọc tiếp
Cho x > 0 và y > 0. Viết biểu thức x 4 5 . x 5 x 6 ; về dạng x m và biểu thức y 4 5 . y 5 y 6 về dạng y n . Ta có m – n = ?
A. -11/6
B. 11/6
C. 8/5
D. -8/5
Trong không gian với hệ tọa độ Oxyz cho A(3;2;1), B(-2;3;6). Điểm
M
(
x
M
;
y
M
;
z
M
)
thay đổi thuộc mặt phẳng (Oxy) . Tìm giá trị của biểu thức
T
x
M
+
y
M
+
z
M
khi
M...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho A(3;2;1), B(-2;3;6). Điểm M ( x M ; y M ; z M ) thay đổi thuộc mặt phẳng (Oxy) . Tìm giá trị của biểu thức T = x M + y M + z M khi M A → + 3 M B → nhỏ nhất
A. - 7 2
B. 7 2
C. 2
D. - 2
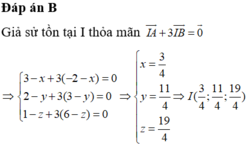
M A → + 3 M B → = 4 M I → ⇒ M A → + 3 M B → m i n ⇒ M I → m i n
Suy ra M là hình chiếu của I lên (Oxy)
⇒ M 3 4 ; 11 4 ; 0 ⇒ T = 14 4 = 7 2
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz cho A(3;2;1), B(-2;3;6). Điểm
M
(
x
M
;
y
M
;
z
M
)
thay đổi thuộc mặt phẳng (Oxy). Tìm giá trị của biểu thức
T
x
M
+
y...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho A(3;2;1), B(-2;3;6). Điểm M ( x M ; y M ; z M ) thay đổi thuộc mặt phẳng (Oxy). Tìm giá trị của biểu thức T = x M + y M + z M k h i M A → + 3 M B → nhỏ nhất.
A. - 7 2
B. 7 2
C. 2.
D. -2.
Đáp án C.
M A → + 3 M B → =
M A → + 3 M B →
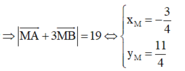
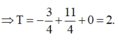
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz cho A (3;2;1), B (-2;3;6). Điểm M (xM; yM; zM) thay đổi thuộc mặt phẳng (Oxy). Tìm giá trị của biểu thức T xM + yM + zM khi
M
A
→
+
3
M
B
→
nhỏ nhất. A. -7/2 B. 7/2 C. 2 D. -2
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho A (3;2;1), B (-2;3;6). Điểm M (xM; yM; zM) thay đổi thuộc mặt phẳng (Oxy). Tìm giá trị của biểu thức T = xM + yM + zM khi M A → + 3 M B → nhỏ nhất.
A. -7/2
B. 7/2
C. 2
D. -2
Phân tích đa thức thành nhân tử : xm + 4 – xm + 3 – x + 1
\(x^{m+4}-x^{m+3}-x+1=x^{m+3}\left(x-1\right)-\left(x-1\right)=\left(x-1\right)\left(x^{m+3}-1\right)\)
Đúng 1
Bình luận (0)
Ta có: \(x^{m+4}-x^{m+3}-x+1\)
\(=x^{m+3}\left(x-1\right)-\left(x-1\right)\)
\(=\left(x-1\right)\left(x^{m+3}-1\right)\)
Đúng 0
Bình luận (0)