cho góc nhọn xOy . Từ I trong góc xOy kẻ In // Ox và Im // Oy. chứng minh góc xOy=góc nIm
có nx vẽ mối quan hệ giữa 2 cạnh của góc đó
3. Cho góc nhọn xOy. Từ điểm I trong góc đó kẻ các tia Im // Ox; In // Oy.
a) Hãy chứng tỏ xOy = mIn.
b) Có nhận xét gì về mối quan hệ giữa các cạnh của 2 góc ấy?
Gíup mình với cảm ơn các bạn nhiều!!!
3. Cho góc nhọn xOy. Từ điểm I trong góc đó kẻ các tia Im // Ox; In // Oy.
a) Hãy chứng tỏ xOy = mIn.
b) Có nhận xét gì về mối quan hệ giữa các cạnh của 2 góc ấy?
Gíup mình với cảm ơn các bạn nhiều!!!
a: Gọi A,B lần lượt là giao của In với Ox, Im với Oy
Xét tứ giác OAIB có
OA//IB
OB//IA
=>OAIB là hình bình hành
=>góc AOB=góc AIB
=>góc xOy=góc mIn
b: OA//IB và OB//IA
=>Mối quan hệ giữa các cặp cạnh của 2 góc đó là song song với nhau
cho góc nhọn xoy oz là tia phân giác của góc đó. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Gọi I là giao điểm của Oz và AB
a, Chứng minh: tam giác OIA = tam giác OIB. Chứng minh Oz và AB
b, Từ I kẻ IN vuông góc Ox và IM vuông góc Oy ( N thuộc Ox, M thuộc Oy). Chứng minh IM = IN
c) Chứng minh: Góc BIM = Góc AIN
d) Chứng minh: MN // AB
a: Xét ΔOIA và ΔOIB có
OA=OB
\(\widehat{AOI}=\widehat{BOI}\)
OI chung
Do đó: ΔOIA=ΔOIB
b: Xét ΔONI vuông tại N và ΔOMI vuông tại M có
OI chung
\(\widehat{NOI}=\widehat{MOI}\)
Do đó: ΔONI=ΔOMI
Suy ra: IN=IM
cho góc nhọn xOy, Oz là tia phân giác của góc đó. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA =OB . Gọi I là giao điểm của Oz và AB.
a) Chứng minh: . tam giác OIA tam giác OIB Chứng minh Oz vuông góc AB .
b) Từ I kẻ IN vuông góc Ox và IM vuông góc Oy ( N thuộc Ox ,M thuộc Oy) . Chứng minh: IM =IN .
c) Chứng minh: góc BIM = góc AIN .
d)Chứng minh: MN // AB
cho góc nhọn xOy và điểm M nằm trong góc đó . Qua M vẽ đường thẳng a//Ox cắt Oy tại A, kẻ đường thẳng b//Oy cắt Kỹ tại B chứng minh góc AMB=góc xOy 
Xét tứ giác BMOA:
+ BM // OA (b // Oy).
+ AM // OB (a // Ox).
\(\Rightarrow\) Tứ giác BMOA là hình bình hành (dhnb).
\(\Rightarrow\widehat{AMB}=\widehat{BOA}\) (Tính chất hình bình hành).
hay \(\Rightarrow\widehat{AMB}=\widehat{xOy.}\)
Cho góc nhọn xOy. Từ điểm A trên cạnh Ox, ta vẽ tia Am song song với tia Oy nằm trong góc xOy. Kẻ tia phân giác On của góc xOy và tia phân giác của góc OAm. Chứng minh: On vuông góc với tia Ap.
Ai lm đúng mik tick cho. Cần Gấp!!!!!!!
ko cần vẽ hình đâu nha!
cho góc nhọn xoy, oz là tia phân giác của góc đó. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Gọi I là giao điểm của Oz và AB
a, Chứng minh: tam giác OIA = tam giác OIB. Chứng minh Oz và AB
b, Từ I kẻ IN vuông góc Ox và IM vuông góc Oy ( N thuộc Ox, M thuộc Oy). Chứng minh IM = IN
c) Chứng minh: Góc BIM = Góc AIN
d) Chứng minh: MN // AB
ai làm nhanh cho mình cả bài với ạ
THANK YOU SO MUCH
a) Xét tam giác \(OIA\) và tam giác \(OIB\) có:
\(OA=OB\)
\(\widehat{AOI}=\widehat{BOI}\)
\(OI\) cạnh chung
suy ra \(\Delta OIA=\Delta OIB\) (c.g.c)
b) Xét tam giác \(OIN\) và tam giác \(OIM\):
\(\widehat{ION}=\widehat{IOM}\)
\(OI\) cạnh chung
\(\widehat{ONI}=\widehat{OMI}\left(=90^o\right)\)
suy ra \(\Delta OIN=\Delta OIM\) (cạnh huyền - góc nhọn)
\(\Rightarrow IN=IM\)
c) \(\Delta OIA=\Delta OIB\) suy ra \(IA=IB\).
Xét tam giác \(INA\) và tam giác \(IMB\):
\(IA=IB\)
\(\widehat{INA}=\widehat{IMB}\left(=90^o\right)\)
\(IN=IM\)
suy ra \(\Delta INA=\Delta IMB\) (cạnh huyền - cạnh góc vuông)
\(\Rightarrow\widehat{AIN}=\widehat{BIM}\)
d) \(\Delta OIN=\Delta OIM\) suy ra \(ON=OM\)
suy ra \(\dfrac{ON}{OA}=\dfrac{OM}{OB}\) suy ra \(MN//AB\).
Cho góc xOy nhọn, điểm A nằm trong góc đó, kẻ Ax'// Ox, Ay'// Oy sao cho góc x'Ay' góc nhọn . Chứng minh góc xOy= x'Ay'.
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
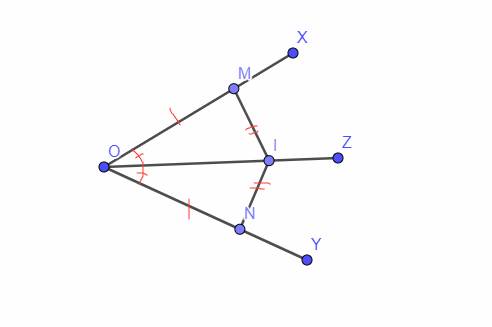
cho góc nhọn xOy. Vẽ tia phân giác Oz của góc xOy. Lấy hai điểm M và N lần lượt thuộc tia Ox và tia Oy sao cho OM=ON. Lấy điểm I bất kỳ thuộc tia Oz. Chứng minh rằng A) tam giác OIM = tam giác OIN B) Góc OIM = Góc OIN C) IM = IN
`a,` Xét Tam giác `OIM` và Tam giác `OIN` có:
`OM = ON (g``t)`
\(\widehat{MOI}=\widehat{NOI}\) `(` tia phân giác \(\widehat{xOy}\) `)`
`OI` chung
`=>` Tam giác `OIM =` Tam giác `OIN (c-g-c)`
`b,` Vì Tam giác `OIM =` Tam giác `OIN (a)`
`->` \(\widehat{OIM}=\widehat{OIN}\) `( 2` góc tương ứng `)`
`c,` Vì Tam giác `OIM =` Tam giác `OIN (a)`
`-> IM = IN (2` cạnh tương ứng `)`
`\color{blue}\text {#DuyNam}`