Cho \(a,b\in\mathbb{Z}\). Tìm số nguyên \(x\), biết :
a) \(b+x=a\)
b) \(b-x=a\)
Những câu hỏi liên quan
Cho \(a,b\in\mathbb{Z}\). Tìm số nguyên \(x\) ,biết :
a) \(a+x=b\)
b) \(a-x=b\)
a) a + x = b
x = b - a (chuyển a sang vế phải)
b) a – x = b
a - b = x (chuyển -x sang vế phải, chuyển b sang vế trái)
x = a - b
Đúng 0
Bình luận (0)
a) a + x = b
x = b - a (chuyển a sang vế phải)
b) a – x = b
a - b = x (chuyển -x sang vế phải, chuyển b sang vế trái)
x = a - b
Đúng 0
Bình luận (0)
Sách Giáo Khoa
Bài giải:
a) x = b - a; b) x = a - b.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hai tập hợp:
\(A = \left\{ {x \in \mathbb{Z}| - 2 \le x \le 3} \right\}\)
\(B = \{ x \in \mathbb{R}|{x^2} - x - 6 = 0\} \)
Tìm \(A\,{\rm{\backslash }}\,B\) và \(B\,{\rm{\backslash }}\,A\).
Ta có: \(A = \left\{ {x \in \mathbb{Z}| - 2 \le x \le 3} \right\} = \{ - 2; - 1;0;1;2;3\} \)
Và \(B = \{ x \in \mathbb{R}|{x^2} - x - 6 = 0\} = \{ - 2;3\} \)
Khi đó:
Tập hợp \(A\,{\rm{\backslash }}\,B\) gồm các phần tử thuộc A mà không thuộc B. Vậy\(A\,{\rm{\backslash }}\,B = \{ - 1;0;1;2\} \).
Tập hợp \(B\,{\rm{\backslash }}\,A\) gồm các phần tử thuộc B mà không thuộc A. Vậy \(B\,{\rm{\backslash }}\,A = \emptyset \)
Đúng 0
Bình luận (0)
Cho \(a\in\mathbb{Z}\). Tìm số nguyên \(x\), biết :
a) \(a+x=5\)
b) \(a-x=2\)
a) a + x = 5
x = 5 - a (chuyển a sang vế phải)
b) a - x = 2
a - 2 = x (chuyển -x sang vế phải, chuyển 2 sang vế trái) hay x = a - 2
Đúng 0
Bình luận (0)
a) a + x = 5
x = 5 - a (chuyển a sang vế phải)
b) a - x = 2
a - 2 = x (chuyển -x sang vế phải, chuyển 2 sang vế trái)
hay x = a - 2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho \(a\in\mathbb{Z}\). Tìm số nguyên \(x\), biết :
a) \(a+x=7\)
b) \(a-x=25\)
Câu a) \(a+x=7\) . Chuyển vế \(a\) ta được :\(x=7-a\)
Câu b) \(a-x=25\) . Chuyển vế \(x\) và 25 ta được : \(a-25=x\) . Vậy \(x=a-25\) .
Đúng 0
Bình luận (0)
a) \(a+x=7\)\(\Rightarrow x=7-a\)
b) \(a-x=25\Rightarrow x=a-25\)
Đúng 0
Bình luận (0)
Cho \(A = \{ x \in \mathbb{R}|{x^2} - 5x - 6 = 0\} ,\)\(B = \{ x \in \mathbb{R}|{x^2} = 1\} .\)
Tìm \(A \cap B,A \cup B,A\backslash B,{\rm{ }}B\backslash A.\)
Phương trình \({x^2} - 5x - 6 = 0\) có hai nghiệm là -1 và 6, nên \(A = \{ - 1;6\} \)
Phương trình \({x^2} = 1\) có hai nghiệm là 1 và -1, nên \(B = \{ - 1;1\} \)
Do đó
\(\begin{array}{l}A \cap B = \{ - 1\} ,\\A \cup B = \{ - 1;1;6\} ,\\A\backslash B = \{ 6\} ,\\B\backslash A = \{ 1\} ,\end{array}\)
Đúng 0
Bình luận (0)
Cho \(A = \{ x \in \mathbb{R}|1 - 2x \le 0\} ,\)\(B = \{ x \in \mathbb{R}|x - 2 < 0\} .\)
Tìm \(A \cap B,A \cup B.\)
Tham khảo:
Ta có:
Bất phương trình \(1 - 2x \le 0\) có nghiệm là \(x \ge \frac{1}{2}\) hay \(A = [\frac{1}{2};+\infty)\)
Bất phương trình \(x - 2 < 0\) có nghiệm là \(x < 2\) hay \(B = ( - \infty ;2)\)
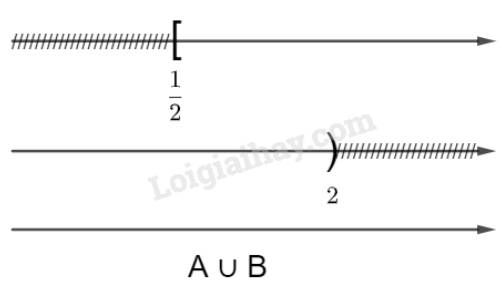
Vậy \(A \cup B = \mathbb R\)
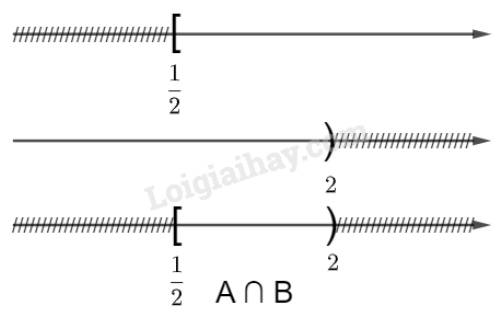
Vậy \(A \cap B = [\frac{1}{2};2)\)
Đúng 0
Bình luận (0)
Cho hai tập hợp:
\(A = \{ x \in \mathbb{Z}| - 3 < x < 3\} ,\)\(B = \{ x \in \mathbb{Z}| - 3 \le x \le 3\} \)
a) Viết tập hợp A, B bằng cách liệt kê các phần tử của tập hợp.
b) Mỗi phần tử của tập hợp A có thuộc tập hợp B không?
a) \(A = \{ - 2; - 1;0;1;2\} \)
\(B = \{ - 3; - 2; - 1;0;1;2;3\} \)
b) Mỗi phần tử của tập hợp A đều thuộc tập hợp B.
Đúng 0
Bình luận (0)
Cho hai tập hợp:
\(\begin{array}{l}A = \{ x \in \mathbb{R}|x \le 0\} ,\\B = \{ x \in \mathbb{R}|x \ge 0\} .\end{array}\)
Tìm \(A \cap B,A \cup B.\)
\(\begin{array}{l}A \cap B = \{ 0\} \\A \cup B = \mathbb{R}\end{array}\)
Đúng 0
Bình luận (0)
64. Cho a \(\in\) \(Z\). Tìm số nguyên x, biết:
a) a + x = 5
b) a- x = 2
65. Cho a, b\(\in Z\). Tìm số nguyên x, biết:
a) a + x = b
b) a - x = b
64. a) a + x = 5
=> x = 5 - a
b) a - x = 2
=> x = a - 2
65. a) a + x = b
=> x = b - a
b) a - x = b
=> x = a - b
Đúng 0
Bình luận (0)
Cau 64:
Chuyen ve
a + x = 5
x = 5 - a
b) a - x = 2
x = a - 2
Đúng 0
Bình luận (0)
bài 64:
a,x=5-a
b,x=a-2
bài65
a,x=b-a
b,x=a-b
Đúng 0
Bình luận (0)