Cho pt: x2-2(m+4)x+m2-8=0. lập hệ thức liên hệ giữa x1,x2 độc lập với m

Những câu hỏi liên quan
Cho pt x^2 - 2 (m-1)x+2m-3=0 gọi x1 x2 là 2 nghiệm của pt tìm hệ thức liên hệ giữa x1 x2 độc lập với m
cho pt: x² -2mx -m² -1=0 Tìm hệ thức liên hệ giữa 2 nghiệm x1;x2 của phương trình độc lập đối vs m
Xem chi tiết
Lời giải:
Theo hệ thức Viet, nếu $x_1,x_2$ là 2 nghiệm của pt $x^2-2xm-m^2-1=0$ thì:
$x_1+x_2=2m$
$x_1x_2=-m^2-1$
\(\Rightarrow \left\{\begin{matrix} (x_1+x_2)^2=4m^2\\ 4x_1x_2=-4m^2-4\end{matrix}\right.\)
$\Rightarrow (x_1+x_2)^2+4x_1x_2=-4$
$\Leftrightarrow x_1^2+x_2^2+6x_1x_2=-4$
Đây chính là biểu thức liên hệ giữa $x_1,x_2$ độc lập với $m$.
Đúng 0
Bình luận (0)
Cho biết pt \(x^2-\left(m-2\right)x+\left(2m-1\right)=0\) có các nghiệm x1 ; x2 .
Lập một hệ thức giữa x1 ; x2 độc lập đối với m.
Theo viet: \(x_1+x_2=m+2\)
\(x_1x_2=2m-1\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x_1+2x_2=2m+4\\x_1x_2=2m-1\end{matrix}\right.\)
Trừ vế cho vế: \(2x_1+2x_2-x_1x_2=5\)
Vậy hệ thức trên độc lập với m.
Đúng 0
Bình luận (0)
Cho phương trình
x
2
-
2
(
m
-
1
)
x
+
m
2
-
3
m
0
Giả sử phương trình có hai nghiệm
x
1
;
x
2
.Tìm hệ thức giữa
x
1
;
x
2
độc lập đối với m.
Đọc tiếp
Cho phương trình x 2 - 2 ( m - 1 ) x + m 2 - 3 m = 0 Giả sử phương trình có hai nghiệm x 1 ; x 2 .Tìm hệ thức giữa x 1 ; x 2 độc lập đối với m.
![]()
![]()
![]()
![]()
Đáp án: A
Theo hệ thức Vi-ét ta có: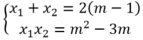
Ta xét các phương án:
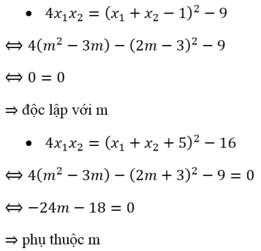
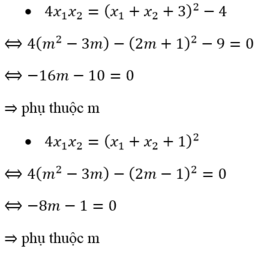
Đúng 0
Bình luận (0)
Cho phương trình
\(\left(m-1\right)x^2-2\left(m-3\right)x+m+1\)1=0
Với điều kiện m để pt có 2 nghhiêm x1, x2 tìm hệ thức liên hệ giữa x1, x2 độc lập với tham số m
đoạn cuối là m + 1 hay m + 11 vậy bạn
Xét
\(\Delta'=\left(m-3\right)^2-\left(m-1\right)\left(m+1\right)=m^2-6m+9-m^2-1=-6m+7\ge0\)
\(\Rightarrow m\le\frac{7}{6}\)
Theo Viete ta có:\(x_1+x_2=\frac{2\left(m-3\right)}{m-1}\left(1\right);x_1x_2=\frac{m+1}{m-1}\)
\(\Leftrightarrow x_1x_2\left(m-1\right)=m+1\Leftrightarrow x_1x_2m-m=1+x_1x_2\)
\(\Leftrightarrow m\left(x_1x_2-1\right)=1+x_1x_2\Leftrightarrow m=\frac{1+x_1x_2}{x_1x_2-1}\)
Thay vào ( 1 ) rồi rút gọn là OK nhá,nhác ko muốn tính :))
Cho phương trình (m-1)x2 - 2(m+1)x + m =0
a) Giải và biện luận pt
b) Khi phương trình có 2 nghiệm phân biệt x1,x2 .Tìm một hệ thức liên hệ giữa x1,x2 độc lập với m. Tìm m sao cho Ix1-x2I>= 2
Xét m=1 phương trình trở thành \(-4x+1=0\)có nghiệm duy nhất x=-1/4
với m#1 ta có \(\Delta'=\left(m+1\right)^2-m\left(m-1\right)=3m+1\)
với \(\hept{\begin{cases}m\ne1\\m>-\frac{1}{3}\end{cases}}\) pt có hai nghiệm phân biệt
với \(m=-\frac{1}{3}\) pt có nghiệm duy nhất
với \(m< -\frac{1}{3}\)pt vô nghiệm,
theo viet ta có \(\hept{\begin{cases}x_1+x_2=\frac{2\left(m+1\right)}{m-1}=2+\frac{4}{m-1}\\x_1x_2=\frac{m}{m-1}=1+\frac{1}{m-1}\end{cases}}\) lấy phương trình trên trừ đi 4 lần phương trình dưới ta có
\(x_1+x_2-4x_1x_2=-2\)
ý sau, ta có \(\left|x_1-x_2\right|=\frac{2\sqrt{\Delta'}}{\left|a\right|}=\frac{2\sqrt{3m+1}}{\left|m-1\right|}>2\)
\(\frac{\Leftrightarrow4\left(3m+1\right)}{\left(m-1\right)^2}\ge4\Leftrightarrow m^2-5m\le0\Rightarrow m\in\left[0,5\right]\)
kết hợp với đk có 2 nghiệm phân biệt ở câu a , ta có \(m\in\left[0,5\right]\backslash\left\{1\right\}\)
Cho phuong trình:
a, x2-(m+2)x+(m-1)=0
b,x2+(4m+1)x+2(m-4)=0
Lập hệ thức liên hệ giữa x1,x2 không phụ thuộc m.
Lời giải:
a. Áp dụng định lý Viet, với $x_1,x_2$ là nghiệm của pt thì:
$x_1+x_2=m+2$
$x_1x_2=m-1$
$\Rightarrow x_1+x_2-x_1x_2=(m+2)-(m-1)=3$
$\Leftrightarrow x_1+x_2-x_1x_2-3=0$ (đây chính là biểu thức liên hệ giữa $x_1,x_2$ mà không phụ thuộc vào $m$)
b.
$x_1+x_2=-(4m+1)$
$x_1x_2=2(m-4)$
$\Rightarrow x_1+x_2+2x_1x_2=-(4m+1)+4(m-4)=-17$
$\Rightarrow x_1+x_2+2x_1x_2+17=0$
Đúng 0
Bình luận (0)
Cho pt: x^2-(m+2)x+(2m-1)=0 có 2 nghệm x1,x2. Lập hệ thức lên hệ giữa x1,x2 không phụ thuộc m.
Cho pt:x2 - 2(m-1)x +2m-3=0
Tìm 1 hệ thức liên hệ giữa 2 nghiệm x1,x2 độc lập với m
\(\left\{{}\begin{matrix}x_1+x_2=2m-2\\x_1x_2=2m-3\end{matrix}\right.\)
Trừ vế cho vế ta được:
\(x_1+x_2-x_1x_2=1\)
Đây là biểu thức liên hệ ko phụ thuộc m
Đúng 0
Bình luận (0)
Cho pt \(x^2-2\left(m-1\right)x+m^2-3m=0\)
a/ tìm m dể pt có nghiệm bằng 0. Tìm nghiệm còn lại
b/ khi pt có nghiệm x1, x2. Tìm hệ thức giữa x1, x2 độc lập với m
a/ Thay \(x=0\) vào pt ta được:
\(m^2-3m=0\Rightarrow\left[{}\begin{matrix}m=0\\m=3\end{matrix}\right.\)
- Khi \(m=0\Rightarrow x^2+2x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
- Khi \(m=3\Rightarrow x^2-4x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
b/ Theo định lý Viet:
\(\left\{{}\begin{matrix}x_1+x_2=2m-2\\x_1x_2=m^2-3m\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m=\frac{x_1+x_2+2}{2}\\x_1x_2=m^2-3m\end{matrix}\right.\)
\(\Rightarrow x_1x_2=\left(\frac{x_1+x_2+2}{2}\right)^2-\frac{3}{2}\left(x_1+x_2+2\right)\)



















