Tính diện tích của hình được giới hạn bởi các đường cong biết OA = OB = R > 0 ?
Những câu hỏi liên quan
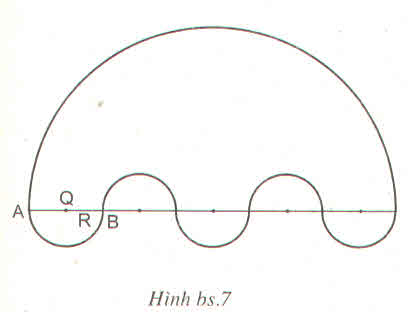
Tính diện tích của hình được giới hạn bởi các đường cong, biết OA = OB = R > 0 (h.bs.7).
Hình đó gồm nửa hình tròn bán kính 5R, 3 nửa hình tròn bán kính R và bớt đi 2 nửa hình tròn bán kính R.
Đúng 0
Bình luận (0)
Biết diện tích hình phẳng giới hạn bởi đường cong yf(x), y0, x2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong yf(2x), trục hoành Ox và hai đường thẳng x0, xa bằng:
Đọc tiếp
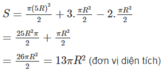
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x), y=0, x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0, x=a bằng:
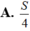
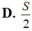
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x),y=0,x=0,x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0,x=a bằng
A. S/4.
B. 4S.
C. 2S.
D. S/2.
Tính diện tích S của hình phẳng (H) giới hạn bởi các đường cong
y
−
x
3
+
12
x
và
y
−
x
2
A.
S
937
12
B.
S
343
12
C.
S
793
4
D.
S...
Đọc tiếp
Tính diện tích S của hình phẳng (H) giới hạn bởi các đường cong y = − x 3 + 12 x và y = − x 2
A. S = 937 12
B. S = 343 12
C. S = 793 4
D. S = 397 4
Chọn A.
Phương pháp
Công thức tính diện tích hình phẳng được giới hạn bởi các đường thẳng
Phương trình hoành độ giao điểm của hai đồ thị hàm số đề bài cho là:
Đúng 0
Bình luận (0)
Tính diện tích S của hình phẳng (H) giới hạn bởi các đường cong
y
-
x
3
+
12
x
và
y
-
x
2
Đọc tiếp
Tính diện tích S của hình phẳng (H) giới hạn bởi các đường cong y = - x 3 + 12 x và y = - x 2
Tính diện tích hình phẳng giới hạn bởi hai đường cong
C
1
:
x
+
4
y
-
y
2
0
C
2
:
x
-
2
y
+
y
2
0
A. 11 B. 10 C. 9 D. 8
Đọc tiếp
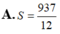
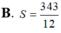
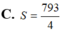
Tính diện tích hình phẳng giới hạn bởi hai đường cong
C 1 : x + 4 y - y 2 = 0 C 2 : x - 2 y + y 2 = 0
A. 11
B. 10
C. 9
D. 8
Phương trình tung độ giao điểm giữa
C 1 : x + 4 y - y 2 = 0 C 2 : x - 2 y + y 2 = 0
là: y 2 - 4 y = 2 y - y 2
⇔ y = 0 y = 3
Vậy S = ∫ 0 3 2 y - y 2 - y 2 - 4 y d y = 9
Đáp án C
Đúng 0
Bình luận (0)
Diện tích hình phẳng giới hạn bởi các đường cong y sin x; y cos x và các đường thẳng
x
0
,
x
π
bằng A.
3
2
B.
2
C.
2
2
D. -
2
2
Đọc tiếp
Diện tích hình phẳng giới hạn bởi các đường cong y = sin x; y= cos x và các đường thẳng x = 0 , x = π bằng
A. 3 2
B. 2
C. 2 2
D. - 2 2
Đáp án C
Giải phương trình: s inx = cos x ⇒ x = π 4 (vì 0 ≤ x ≤ π )
S = ∫ 0 π s inx − cos x d x = 2 2
Đúng 0
Bình luận (0)
Diện tích hình phẳng được giới hạn bởi đường cong y = x 2 và đường thẳng y = 2 x + 3 , trục hoành trong miền x ≥ 0 bằng
A. 12
B. 32 3
C. 9
D. 5 3
Đáp án C
Phương trình hoành độ giao điểm hai đồ thị là
Đúng 0
Bình luận (0)
Diện tích hình phẳng được giới hạn bởi đường cong
y
x
2
và đường thẳng
y
2
x
+
3
, trục hoành trong miền
x
≥
0
bằng A. 12 B. 9 C.
5
3
D.
32
3
Đọc tiếp
Diện tích hình phẳng được giới hạn bởi đường cong y = x 2 và đường thẳng y = 2 x + 3 , trục hoành trong miền x ≥ 0 bằng
A. 12
B. 9
C. 5 3
D. 32 3
