Tìm MAX,MIN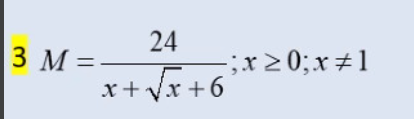
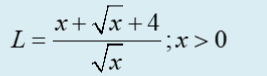
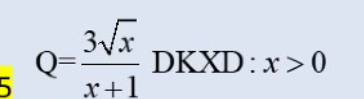

Những câu hỏi liên quan
Tìm Max, min của P=6x-8/x^2+1
Tìm min, max của P=4x+3/x^2+1
mn cho tui hỏi cái
tìm min max của |f(x)| ý
sao Max lại tìm theo 2TH còn min lại tìm theo so sánh trên dưới với trục ox vậy
tai sao lại không thể làm theo cách của tìm max
dạng mà tìm tham số m để hàm số |f(x)| có Min/Max trên [a,b] ý
a) \(a^2+b^2=1\)
Tìm min/max F = \(\dfrac{a}{b+2}\)
b)\(2a^2-2ab+5b^2=1\)
Tìm min/max G = \(\dfrac{\left(a+b\right)}{a-2b+2}\)
a.
\(F=\dfrac{a}{b+2}\Rightarrow F.b+2F=a\)
\(\Rightarrow2F=a-F.b\)
\(\Rightarrow4F^2=\left(a-F.b\right)^2\le\left(a^2+b^2\right)\left(1^2+F^2\right)=F^2+1\)
\(\Rightarrow3F^2\le1\)
\(\Rightarrow-\dfrac{1}{\sqrt{3}}\le F\le\dfrac{1}{\sqrt{3}}\)
Dấu "=" lần lượt xảy ra tại \(\left(a;b\right)=\left(-\dfrac{\sqrt{3}}{2};-\dfrac{1}{2}\right)\) và \(\left(\dfrac{\sqrt{3}}{2};-\dfrac{1}{2}\right)\)
b. Đặt \(\left\{{}\begin{matrix}a+b=x\\a-2b=y\end{matrix}\right.\) quay về câu a
Đúng 3
Bình luận (0)
Viết chương trình nhập vào một dãy n số nguyên khác nhau từ bàn phím. Tìm min, max của dãy và số lần xuất hiện của min, max đó.
Tìm min hoặc max của 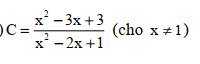
Lời giải:
$C=\frac{x^2-3x+3}{x^2-2x+1}$
$\Rightarrow C(x^2-2x+1)=x^2-3x+3$
$\Leftrightarrow x^2(C-1)+x(3-2C)+(C-3)=0(*)$
Coi $(*)$ là pt bậc 2 ẩn $x$. Vì $C$ tồn tại nên $(*)$ có nghiệm.
$\Leftrightarrow \Delta'=(3-2C)^2-4(C-3)(C-1)\geq 0$
$\Leftrightarrow 4C-3\geq 0$
$\Leftrightarrow C\geq \frac{3}{4}$
Vậy $C_{\min}=\frac{3}{4}$
Đúng 2
Bình luận (0)
giải hộ em
a,Tìm min, max: 4x-16 căn x+4y-22 căn y-4 căn xy+36
b, tìm max :B= 6 cẵn+3/2x+4
c, Tìm Min : C=2/1-x+1/x
a) Tìm min max A = \(\frac{4x+3}{x^2+1}\)
b) Cho x + y = 15 Tìm min max B = \(\sqrt{x-4}+\sqrt{y-3}\)
1)TÌM H min = \(\sqrt{x^2+4}+\sqrt{x^2+8x+17}\)
2) tìm G min,max A=3x+x\(\sqrt{5-x^2}\)
3)tìm min,max B=\(\sqrt{5x-x^2}+\sqrt{18+3x-x^2}\)
câu 1
ta có .....
lười viết Min - cốp xki nha
Đúng 0
Bình luận (0)
DKXD của A, ta có \(x^{2\le5\Rightarrow-\sqrt{5}\le x\le\sqrt{5}}\)
mà \(3x\ge-3\sqrt{5}\)
mặt kkhác \(\sqrt{5-x^2}\ge0\Rightarrow A=3x+x\sqrt{5-x^2}\ge-3\sqrt{5}\)
min A= \(-3\sqrt{5}\)\(\Leftrightarrow x=-\sqrt{5}\)
Đúng 0
Bình luận (0)
ta có \(A^2\le25\)và ta cx có \(-5\le A\le5\)
nhưng dễ thấy \(A=-5\)không xảy ra, vô lí nên ...........bạn xem đoạn sau nhé ( tiếp phần kia )
Đúng 0
Bình luận (0)
+) Tìm min
\(E=\dfrac{1+\sqrt[3]{x}+\sqrt[3]{y}+\sqrt[3]{z}}{xy+yz+zx}\)
+) Tìm max và min
\(F=\dfrac{a-b}{c}+\dfrac{b-c}{a}+\dfrac{c-a}{b}\)
Trong đó a,b,c>0 và \(min\left\{a,b,c\right\}\ge\dfrac{1}{4}max\left\{a,b,c\right\}\)















