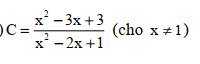Lời giải:
$C=\frac{x^2-3x+3}{x^2-2x+1}$
$\Rightarrow C(x^2-2x+1)=x^2-3x+3$
$\Leftrightarrow x^2(C-1)+x(3-2C)+(C-3)=0(*)$
Coi $(*)$ là pt bậc 2 ẩn $x$. Vì $C$ tồn tại nên $(*)$ có nghiệm.
$\Leftrightarrow \Delta'=(3-2C)^2-4(C-3)(C-1)\geq 0$
$\Leftrightarrow 4C-3\geq 0$
$\Leftrightarrow C\geq \frac{3}{4}$
Vậy $C_{\min}=\frac{3}{4}$
Đúng 2
Bình luận (0)