Hình thoi ABCD có \(\widehat{A}=60^0\). Trên cạnh AD lấy điểm M, trên cạnh DC lấy điểm N sao cho AM = DN. Tam giác BMN là tam giác gì ? Vì sao ?

Những câu hỏi liên quan
Bài 1: Hình thoi ABCD có góc A = 60 độ . Trên cạnh AD lấy điểm M, trên cạnh DC lấy điểm N sao cho AM= DN . Hỏi tam giác BMN là tam giác gì , vì sao?
Xét ΔABD có AB=AD và góc A=60 độ
=>ΔABD đều
=>góc ABD=góc ADB=60 độ và AB=AD=BD
Xét ΔBCD có CB=CD và góc C=60 độ
nên ΔBCD đều
=>BD=CB=CD và góc CBD=góc CDB=60 độ
Xét ΔBAM và ΔBDN có
BA=BD
góc BAM=góc BDN
AM=DN
=>ΔBAM=ΔBDN
=>BM=BN và góc ABM=góc DBN
=>góc DBN+góc DBM=60 độ
=>góc MBN=60 độ
=>ΔMBN đều
Đúng 1
Bình luận (0)
Hình thoi ABCD có góc A = 60°. Trên cạnh AD lấy điểm M, trên cạnh CD lấy điểm N sao cho AM = DN. Tam giác BMN là tam giác gì? Vì sao?
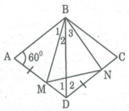
Nối BD, ta có AB = AD (gt)
Suy ra ∆ ABD cân tại A
Mà ∠ A = 60 0 ⇒ ∆ ABD đều
⇒ ∠ (ABD) = ∠ D 1 = 60 0 và BD = AB
Suy ra: BD = BC = CD
⇒ ∆ CBD đều ⇒ ∠ D 2 = 60 0
Xét ∆ BAM và ∆ BDN,ta có:
AB = BD ( chứng minh trên)
∠ A = ∠ D 2 = 60 0
AM = DN (giả thiết)
Do đó ∆ BAM = ∆ BDN ( c.g.c) ⇒ ∠ B 1 = ∠ B 3 và BM = BN
Suy ra ΔBMN cân tại B.
Mà ∠ B 2 + ∠ B 1 = ∠ (ABD) = 60 0
Suy ra: ∠ B 2 + ∠ B 3 = ∠ B 2 + ∠ B 1 = 60° hay ∠ (MBN) = 60 0
Vậy ∆ BMN đều
Đúng 1
Bình luận (0)
Bài 1: Hình thoi ABCD có góc A = 60 độ . Trên cạnh AD lấy điểm M, trên cạnh DC lấy điểm N sao cho AM= DN . Hỏi tam giác BMN là tam giác gì , vì sao?
Bài 2: Cho hình thang ABCD( AB//CD) . Gọi EFGH theo thứ tự lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Hỏi tứ giác EFGH là hình gì, vì sao?
giải giúp mình với ạ
cho hình thoi ABCD có góc a bằng 60 độ .trên AD lấy điểm M, trên CD lấy điểm N sao cho AM=DN. Tam giác BMN là tam giác gì
Cho hình thoi ABCD có \(\widehat{A}=60^{^0}\). Trên các cạnh AD và CD, lấy các điểm M và N sao cho AM + CN = AD.
a) CMR tam giác BMN đều
b) Gọi P là điểm đối xứng của N qua BC. Chứng minh MP song song với CD.
hình thoi abcd có a=60,trên cạnh ad lấy điểm M trên cạnh DC lấy điểm N sao cho AM=DN.tam giác BNM là tam giạc j
bài 1: Cho hình tam giác ABCD vuông tại A có D là điểm đối xứng của A qua BC, AD cắt BC tại H, vẽ E thuộc HC sao cho HEHB. Vẽ EM vuông góc AC.a) Cmr: ABDE là hình thoib) Cmr: D, E, M thẳng hàngc) Cmr: AE vuông góc DCd) Gọi I là trung điểm EC. Cmr: MH vuông góc MIbài 2: Cho hình thoi ABCD có góc A bằng 600, lấy M thuộc AD, N thuộc DC sao cho AMDN. Tam giác BMN là tam giác gì? Vì sao?
Đọc tiếp
bài 1: Cho hình tam giác ABCD vuông tại A có D là điểm đối xứng của A qua BC, AD cắt BC tại H, vẽ E thuộc HC sao cho HE=HB. Vẽ EM vuông góc AC.
a) Cmr: ABDE là hình thoi
b) Cmr: D, E, M thẳng hàng
c) Cmr: AE vuông góc DC
d) Gọi I là trung điểm EC. Cmr: MH vuông góc MI
bài 2: Cho hình thoi ABCD có góc A bằng 600, lấy M thuộc AD, N thuộc DC sao cho AM=DN. Tam giác BMN là tam giác gì? Vì sao?
cho hình tam giác ABCD ư viết lại đề bài đi bạn
Đúng 0
Bình luận (0)
câu 2
tam giác ABM bằng tam giác DBN (c.g.c) nên BM=BN và ABM=DBN ta có ABM+MBD=60 nên DBN+MBD=60 hay MBN =60 tam giác MBN đều
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Trên cạnh AB lấy điểm E và trên cạnh CD lấy điểm F sao cho AE = CF. Trên cạnh AD lấy điểm M và trên cạnh BC lấy điểm N sao cho AM = CN.
Tứ giác AECF là hình gì ? vì sao? Tứ giác MENF là hình gì? Vì sao?
Vì AE=CF và AE//CF (AB//CD do hbh ABCD) nên AECF là hbh
\(\left\{{}\begin{matrix}AE=CF\\AM=CN\\\widehat{A}=\widehat{C}\left(hbh.ABCD\right)\end{matrix}\right.\Rightarrow\Delta AME=\Delta CNF\left(c.g.c\right)\\ \Rightarrow ME=NF\left(4\right)\\ \left\{{}\begin{matrix}AE=CF\\AB=CD\end{matrix}\right.\Rightarrow AB-AE=CD-CF\Rightarrow BE=DF\left(1\right)\\ \left\{{}\begin{matrix}AM=CN\\AD=BC\end{matrix}\right.\Rightarrow AD-AM=CN-BC\Rightarrow DM=BN\left(2\right)\)
ABCD là hbh nên \(\widehat{B}=\widehat{D}\left(3\right)\)
\(\left(1\right)\left(2\right)\left(3\right)\Rightarrow\Delta DMN=\Delta BFE\left(c.g.c\right)\\ \Rightarrow MN=EF\left(5\right)\)
(4)(5) suy ra MENF là hbh
Đúng 0
Bình luận (0)
cho hình chữ nhật ABCD có AB = 18 cmAD = 2/3 AB.Trên AB lấy điểm M sao cho AM = 1/3 ABtreen cạnh CD lấy điểm N sao cho DN = 2/3 DC
a) tính diện tích hình AMND
b)trên cạnh AD lấy điểm K sao cho AK = 2 KD.Tính diện tích hình tam giác KMN
a) Độ dài cạnh AD là :
18 x 2/3 = 12 ( cm )
Độ dài cạnh AM là :
18 x 1/3 = 6 ( cm )
Độ dài cạnh DN là :
18 x 2/3 = 12 ( cm )
Diện tích hình thang AMND là :
( 6 + 12 ) x 12 : 2 = 108 ( cm2)
b) Độ dài cạnh AK là :
12 x 2/3 = 8 ( cm )
Diện tích tam giác AMK là :
6 x 8 : 2 = 24 ( cm2)
Độ dài cạnh KD là :
12 - 8 = 4 ( cm )
Diện tích tam giác KDN là :
4 x 12 : 2 = 24 ( cm2)
Diện tích tam giác KMN là :
108 - 24 - 24 = 60 ( cm2)
Đáp số : a) 108 cm2
b) 60 cm2
Đúng 0
Bình luận (0)





















