M = 6x²+3xy- 2y²- 5 +3y² - 2x²-3xy+5

   = (6x²- 2x²) + ( 3xy -3xy) + ( - 2y²- 2y²)+ (- 5+5)

   = 4x²+ y²

Mà 4x² >0

      y²> 0

Vậy....

\(=\dfrac{3x\left(-x^2\right)}{3x}+\dfrac{2}{3x}-\dfrac{3x}{3x}=\dfrac{-3x^3+2-3x}{3x}\)

\(=\dfrac{-x^2+2-3x}{1}=-\left(x^2-2+3x\right)\)

vậy bt A luôn......

\(a,x^4-2x^3+6x^2+x+14\\ =\left(x^4-3x^3+7x^2\right)+\left(x^3-3x^2+7x\right)+\left(2x^2-6x+14\right)\\ =\left(x^2-3x+7\right)\left(x^2+x+2\right):\left(x^2-3x+7\right)=x^2+x+2\)

Ta có \(x^2+x+2=x^2+x+\dfrac{1}{4}+\dfrac{7}{4}=\left(x+\dfrac{1}{2}\right)^2+\dfrac{7}{4}\ge\dfrac{7}{4}>0\)

Vậy ...

\(b,A=x^3+3xy+y^3\\ A=\left(x+y\right)\left(x^2-xy+y^2\right)+3xy\\ A=x^2-xy+y^2+3xy\\ A=x^2+2xy+y^2=\left(x+y\right)^2=1\)

Ta có: 

\(2x+y=11z\) và \(3x-y=4z\)

Chia theo vế ta có:

\(\dfrac{2x+y}{3x-y}=\dfrac{11z}{4z}=\dfrac{11}{4}\)

\(\Leftrightarrow4\left(2x+y\right)=11\left(3x-y\right)\)

\(\Leftrightarrow8x+4y=33x-11y\)

\(\Leftrightarrow15y=25x\)

\(\Leftrightarrow3y=5x\)

\(\Leftrightarrow\dfrac{x}{3}=\dfrac{y}{5}=k\)

\(\Rightarrow x=3k,y=5k\)

 Thay vào Q ta có:

\(Q=\dfrac{2\cdot\left(3k\right)^2-3\cdot3k\cdot5k}{\left(3k\right)^2+3\cdot\left(5y\right)^2}\)

\(Q=\dfrac{18k^2-45k^2}{9k^2+75k^2}\)

\(Q=\dfrac{k^2\left(18-45\right)}{k^2\left(9+75\right)}\)

\(Q=\dfrac{-27}{84}=-\dfrac{9}{28}\)

\(\dfrac{2x+y}{3x-y}=\dfrac{11}{4}\)

=>33x-11y=8x+4y

=>25x=15y

=>5x=3y

=>x/3=y/5=k

=>x=3k; y=5k

\(Q=\dfrac{2\cdot9k^2-3\cdot3k\cdot5k}{9k^2+3\cdot25k^2}=\dfrac{18-9\cdot5}{9+3\cdot25}=\dfrac{-9}{28}\)

Không biê

a) Ta có: x4 - 1 = (x2 + 1)(x2-1), trong đó : x2 + 1 > 0, với mọi x.

Vậy điều kiện : x2 – 1 ≠ 0

x2 – 1 = (x – 1)(x + 1) ≠ 0 ⇒ x ≠ ±1

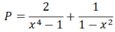
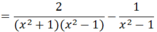
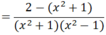
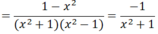
Do x2 + 1 > 0 với mọi x nên P < 0 với mọi x ≠ ±1

a: \(A=x^3-27-x^3+3x^2-3x+1-4\left(x^2-4\right)-x\)

\(=3x^2-4x-26-4x^2+16\)

\(=-x^2-4x-10\)

\(-2x^2+3x-4=-2\left(x^2-\dfrac{3}{2}x+\dfrac{9}{16}\right)-\dfrac{23}{8}=-2\left(x-\dfrac{3}{4}\right)^2-\dfrac{23}{8}\le-\dfrac{23}{8}< 0\)

hello mik biết giải bài này nhưng bn phải viết rõ