Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB
Chứng minh \(\Delta AMN=\Delta BMN\)
Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB
Chứng minh \(\Delta AMN=\Delta BMN\)
Hướng dẫn:

Vì M thuộc đường trung trực của AB
=> MA = MB
N thuộc đường trung trực của AB
=> NA = NB
Do đó ∆AMN = ∆BMN (c.c.c)
47. Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB. Chứng minh
∆AMN = ∆BMN.
Hướng dẫn:

Vì M thuộc đường trung trực của AB
=> MA = MB
N thuộc đường trung trực của AB
=> NA = NB
Do đó ∆AMN = ∆BMN (c.c.c)

Vì M nằm trên đường trung trực của AB nên MA = MB (Định lý 1)
Vì N nằm trên đường trung trực của AB nên NA = NB (Định lý 1)
Xét \(\Delta AMN\)và \(\Delta BMN\)có:
MA = MB (cmt)
NA = NB (cmt)
MN chung
\(\Rightarrow\Delta AMN=\Delta BMN\) (c.c.c)
Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB
Chứng minh \(\Delta AMN=\Delta BMN\)

Vì M thuộc đường trung trực của AB
=> MA = MB
N thuộc đường trung trực của AB
=> NA = NB
Do đó ∆AMN = ∆BMN (c.c.c)
Vì M, N thuộc đường trung trực của AB nên MA = MB; NA = NB
Xét tam giác AMN và tam giác BMN có:
MA = MB
NA = NB
MN chung
=> Tam giác AMN = Tam giác BMN (c.c.c)
vì M và N nằm trên đường trung trực của AB nên M và N cách đều 2 điểm A và B, hay AN=NB; AM=MB.
xát tam giác ANM và tam giác BNM có:
AN=NB (cmt)
AM=MB(cmt)
MN: chung
do đó tam giác ANM= tam giác BNM (c-c-c)
Cho 2 điểm M,N nằm trên đường trung trực của đoạn thẳng AB. Chứng minh tam giác AMN= tam giác BMN
xét tam giác AMN và tam giác BMN có:
MA = MB ( M thuộc đường trung trực d)
NA = NB ( N thuộc đường trung trực d)
MN là cạnh chung
vậy tam giác AMN = tam giác BMN (c.c.c)
1 đúng nhé

Vì M thuộc đường trung trực của AB
=> MA = MB
N thuộc đường trung trực của AB
=> NA = NB
Do đó ∆AMN = ∆BMN (c.c.c)
Cho hai điểm M và N nằm trên đường trung trực d của đoạn thẳng EF. Chứng minh rẳng \(\Delta EMN=\Delta FMN\)
Tham khảo:

Vì M thuộc trung trực EF nên ME = MF ( tính chất điểm thuộc trung trực )
Tương tự \( \Rightarrow \) NE = NF ( tính chất điểm thuộc trung trực )
Xét 2 tam giác MEN và MFN có :
MN là cạnh chung
ME = MF
NE = NF
\(\Rightarrow \Delta MEN = \Delta MFN (c-c-c)\)
Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB. Chứng minh ΔAMN = Δ BMN.
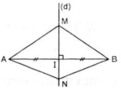
Vì M thuộc đường trung trực của AB
⇒ MA = MB (định lý thuận về tính chất của các điểm thuộc đường trung trực)
N thuộc đường trung trực của AB
⇒ NA = NB (định lý thuận về tính chất của các điểm thuộc đường trung trực)
Do đó ΔAMN và ΔBMN có:
AM = BM (cmt)
MN chung
AN = BN (cmt)
⇒ ΔAMN = ΔBMN (c.c.c)
Cho hai điểm M,N nằm trên đường trung trực của đoạn thẳng AB
Chứng minh tam giác AMN = tam giác BMN
Ta có: M nằm trên đường trung trực của AB
nên MA=MB
Ta có: N nằm trên đường trung trực của AB
nên NA=NB
XétΔAMN và ΔBMN có
MN chung
MA=MB
NA=NB
DO đó: ΔAMN=ΔBMN
Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB.
Chứng minh tam giác AMN = tam giác BMN
Do M,N nằm trên đường trung trực của đoạn AB
=>MA=MB(Tính chất đường trung trực)
NA=NB(Tính chất đường trung trực)
Xét tam giác AMN và tam giác BMN có:
MA=MB
NA=NB
MN chung
=>\(\Delta AMN=\Delta BMN\left(c.c.c\right)\left(đpcm\right)\)
cho ΔABC , M là trung điểm của AB , kẻ đường thẳng đi qua M song song với BC cắt AC tại N . Từ N kẻ đường thẳng song song với AB cắt BC tại P . Chứng minh
a)ΔBMN = ΔNPB và AM = NP
b) ΔAMN = ΔNPC và AN = NC
a: Xét tứ giác BMNP có
MN//BP
NP//BM
Do đó: BMNP là hình bình hành
=>NP=BM=AM
Xét ΔABC có
M là trung điểm của AB
MN//BC
Do đó: N là trung điểm của AC
Xét ΔBMN và ΔNPB có
BM=NP
MN=PB
BN chung
DO đó: ΔBMN=ΔNPB
b: Xét ΔAMN và ΔNPC có
AM=NP
MN=PC
AN=NC
Do đó: ΔAMN=ΔNPC
Cho M,N là hai điểm phân biệt nằm trên đường trung trực của cạnh AB sao cho AM=BN. O là giao điểm của MN và AB. Chứng minh:
a. \(\Delta\)AMO = \(\Delta\)BNO
b. Tam giác AMN cân.
c. Nếu góc AMO=30o thì tam giác AMB là tam giác đều
a: Xét ΔAMO vuông tại O và ΔBNO vuông tại O có
OA=OB
AM=BN
Do đó: ΔAMO=ΔBNO
b: MN là trung trực của AB
=>MA=MB; NA=NB
mà MA=NB
nen MA=AN
=>ΔAMN cân tại A
c: góc AMB=2*30=60 độ
=>ΔMAB đều