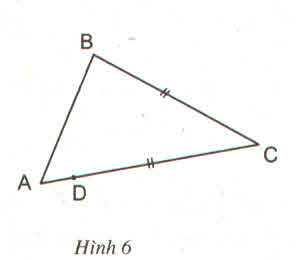
Xem hình 6, có hai đoạn thẳng bằng nhau BC và DC. Hỏi rằng kết luận nào trong các kết luận sau là đúng ? Tại sao ?
a) \(\widehat{A}=\widehat{B}\)
b) \(\widehat{A}>\widehat{B}\)
c) \(\widehat{A}< \widehat{B}\)
Trong Hình 9.6 có hai đoạn thẳng BC và DC bằng nhau, D nằm giữa A và C. Hỏi kết luận nào trong các kết luận sau là đúng? Tại sao?

\(\begin{array}{l}a)\widehat A = \widehat B\\b)\widehat A > \widehat B\\c)\widehat A < \widehat B\end{array}\)
Vì BC = DC.
Mà D nằm giữa A và C nên AC = DA + DC, do đó AC > DC
\( \Rightarrow \)AC > BC
Xét tam giác ABC có AC > BC
\( \Rightarrow \widehat B > \widehat A\) ( trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn)
Vậy khẳng định c là đúng.
Trên hình 7, hai đường thẳng a, b song song với nhau, đường thẳng c cắt a tại A và cắt b tại B
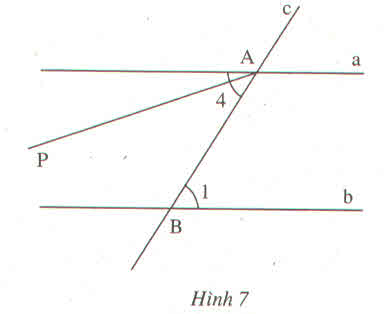
a) Lấy một cặp góc so le trong (chẳng hạn cặp \(A_4,B_1\)) rồi đo xem hai góc đó có bằng nhau hay không
b) Hãy lí luận vì sao \(\widehat{A}_4=\widehat{B}_1\) theo gợi ý sau :
- Nếu \(\widehat{A}_4\ne\widehat{B}_1\) thì qua A ta vẽ tia AP sao cho \(\widehat{PAB}=\widehat{B}_1\)
- Thế thì AP // b, vì sao ?
- Qua A, vừa có a // b, vừa có AP // b, thì sao ?
- Kết luận : Đường thẳng AP và đường thẳng a chỉ là một. Nói cách khác \(\widehat{PAB}=\widehat{A}_4\), từ đó \(\widehat{A}_4=\widehat{B}_1\)
Xem hình 6, có hai đoạn bằng nhau BC và DC. Hỏi rằng kết luận nào trong các kết luận sau là đúng? Tại sao?
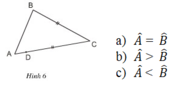
Vì D nằm giữa A và C (giả thiết)
⇒ AC = AD + DC = AD + BC (DC = BC theo đề bài)
⇒ AC > BC
Mà trong tam giác ABC :
Góc đối diện cạnh AC là góc B
Góc đối diện cạnh BC là góc A
Ta lại có: AC > BC (cmt)
⇒ B̂ > Â (theo định lí 1)
Hay  < B̂.
Vậy kết luận c) là đúng.
Cho hai tam giác ABC và A’B’C’ (Hình 57) có: \(\widehat A = \widehat {A'} = 60^\circ \), AB = A’B’ = 3 cm, \(\widehat B = \widehat {B'} = 45^\circ \). Bằng cách đếm số ô vuông, hãy so sánh BC và B’C’. Từ đó có thể kết luận được hai tam giác ABC và A’B’C’ bằng nhau hay không?
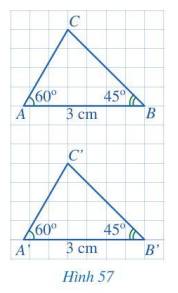
BC = B’C’ = 4 (đường chéo của 4 ô vuông).
Tam giác ABC và tam giác A’B’C’ có: BC = B’C’, AB = A’B’, \(\widehat B = \widehat {B'}\).
Vậy \(\Delta ABC = \Delta A'B'C'\)(c.g.c)
Trong Hình 95, đường thẳng a là đường trung trực của hai đoạn thẳng AB và CD. Chứng minh:

a) AB // CD;
b) \(\Delta MNC = \Delta MND;\)
c) \(\widehat {AMD} = \widehat {BMC}\);
d) \(AD = BC,\widehat A = \widehat B\);
e) \(\widehat {ADC} = \widehat {BCD}\).
a) Ta có: đường thẳng a là đường trung trực của đoạn thẳng AB và CD nên \(a \bot AB;a \bot CD\).
Suy ra: AB // CD.
b) Đường thẳng a là đường trung trực của đoạn thẳng AB và CD nên MN là đường trung trực của đoạn thẳng AB và CD. Suy ra: MD = MC.
Xét tam giác vuông MNC và tam giác vuông MND có: ND = NC; MD = MC.
Vậy \(\Delta MNC = \Delta MND\)(cạnh huyền – cạnh góc vuông).
c) \(\Delta MNC = \Delta MND\)nên \(\widehat {CMN} = \widehat {DMN}\).
Mà \(\widehat {AMN} = \widehat {BMN} = 90^\circ \Rightarrow \widehat {AMN} - \widehat {DMN} = \widehat {BMN} - \widehat {CMN}\).
Vậy \(\widehat {AMD} = \widehat {BMC}\).
d) Xét hai tam giác AMD và BMC có:
MA = MB;
\(\widehat {AMD} = \widehat {BMC}\);
MD = MC.
Vậy \(\Delta MAD = \Delta MBC\)(c.g.c). Suy ra: \(AD = BC,\widehat A = \widehat B\) (cặp cạnh và góc tương ứng).
e) \(\Delta MAD = \Delta MBC\) nên \(\widehat {ADM} = \widehat {BCM}\) (2 góc tương ứng).
\(\Delta MNC = \Delta MND\) nên \(\widehat {MCN} = \widehat {MDN}\) (2 góc tương ứng).
Vậy \(\widehat {ADM} + \widehat {MDN} = \widehat {BCM} + \widehat {MCN}\) hay \(\widehat {ADC} = \widehat {BCD}\).
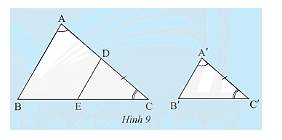
Cho hai tam giác \(ABC\) và \(A'B'C'\) có \(\widehat A = \widehat {A'},\widehat C = \widehat {C'}\) (Hình 9).
Trên cạnh \(AC\), lấy điểm \(D\) sao cho \(DC = A'C'\). Qua \(D\) là kẻ đường thẳng song song với \(AB\) cắt cạnh \(BC\) tại \(E\).
a) Tam giác \(DEC\) có đồng dạng với tam giác \(ABC\) không?
b) Nhận xét về mối quan hệ giữa tam giác \(A'B'C'\)và tam giác \(DEC\).
c) Dự đoán về sự đồng dạng của hai tam giác \(A'B'C'\)và \(ABC\).
a) Vì \(ED//AB \Rightarrow \Delta DEC\backsim\Delta ABC\) (định lí)
b) Vì \(ED//AB \Rightarrow \widehat {CDE} = \widehat {CAB}\) (hai góc đồng vị)
Mà \(\widehat {CAB} = \widehat {A'}\). Do đó, \(\widehat {CDE} = \widehat {B'A'C'}\).
Xét tam giác \(A'B'C'\) và tam giác \(DEC\) ta có:
\(\widehat {B'A'C'} = \widehat {CDE}\) (chứng minh trên)
\(A'C' = CD\) (giải thuyết)
\(\widehat {C'} = \widehat C\) (giả thuyết)
Do đó, \(\Delta A'B'C' = \Delta DEC\) (g.c.g)
c) Vì tam giác \(\Delta A'B'C'\backsim\Delta DEC\) (tính chất)
Mà \(\Delta DEC\backsim\Delta ABC\) nên \(\Delta ABC\backsim\Delta A'B'C'\).
Cho tam giâc ABC và tam giác có ba đỉnh là D, E, F. Biết AB = DF và \(\widehat{B}=\widehat{D}\)
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai ?
a) Nếu \(\widehat{A}=\widehat{F}\) thì hai tam giác đó bằng nhau
b) Nếu \(\widehat{A}=\widehat{E}\) thì hai tam giác đó bằng nhau
c) Nếu \(\widehat{C}=\widehat{E}\) thì hai tam giác đó bằng nhau
Trong các khẳng định sau:
- Khẳng định c) là đúng.
- Khẳng định a) ; b) là sai.
Cho hai tam giác ABC và A’B’C’ (Hình 47) có: AB = A’B’ = 2 cm, \(\widehat A = \widehat {A'} = 60^\circ \), AC = A’C’ = 3 cm. Bằng cách đếm số ô vuông, hãy so sánh BC và B’C’. Từ đó có thể kết luận được hai tam giác ABC và A’B’C’ bằng nhau hay không?
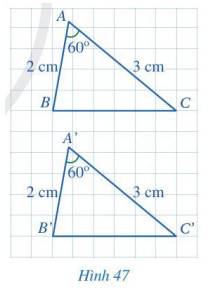
BC = B’C’ = 6 (ô vuông).
Tam giác ABC và A’B’C’ có các cặp cạnh tương ứng bằng nhau nên tam giác ABC bằng tam giác A’B’C’ (c.c.c)
1. Cho hình vẽ, biết AD//BC. \(\widehat{A}\)= 90. \(\widehat{D}\)=800. Số đo các \(\widehat{ABC}\)và \(\widehat{BCD}\)là:......
2. Cho hình vẽ. Điều kiện nào thì a//b:
3. Cho hình vẽ. Kết luận nào sau đây là sai?
a. \(\widehat{O_1=\widehat{O_3}}\) b. \(\widehat{O_2=\widehat{O_1}}\)
c.\(\widehat{O_2}\)= 870 d. \(\widehat{O_1}\)=870
Hình em sẽ trả lời bên dưới nha! nhanh lên em cần gấp lắm, đợi em vẽ hình nhé!
1. Vì đường thẳng A \(\perp\) với đường thẳng B
\(\Rightarrow\widehat{ABC}=90^o\)
Vì \(\widehat{C}\) và \(\widehat{D}\)là hai góc so le trong
\(\Rightarrow\widehat{C}=\widehat{D}=80^o\)
Vì \(\widehat{C}\)và \(\widehat{BCD}\)kề bù
\(\Rightarrow\widehat{C}+\widehat{BCD}=180^o\)
Mà \(\widehat{C}=80^o\)
\(\Rightarrow80^o+\widehat{BCD}=180^o\)
\(\Rightarrow\widehat{BCD}=180^o-80^o=100^o\)
2. Để a // b thì:
- Một cặp góc so le trong (ví dụ \(\widehat{A3}\)và\(\widehat{B3}\)) bằng nhau
- Hoặc một cặp góc đồng vị (VD \(\widehat{A1}\)và \(\widehat{B1}\)) bằng nhau
- Hoặc một cặp trong cùng phía (VD \(\widehat{A2}\)và\(\widehat{B3}\)) bù nhau (có tổng số đo = 180o )