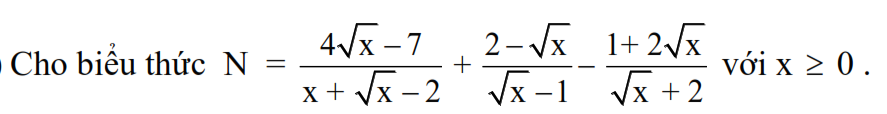
a) Tìm x để N=\(\dfrac{1}{2}\)
b) Tìm x ∈ \(Z\) sao cho N ∈ \(Z\)
c) Tìm GTLN của N
a,Tìm a,b ∈ Z biết A (b+1) =3
b, tìm n ∈ Z sao cho 2n+7 ⋮ n+1
c, tìm x,y ∈ Z sao cho xy + x-y =6
\(\dfrac{help}{me}\)
a) \(a\left(b+1\right)=3\left(a;b\inℤ\right)\)
\(\Rightarrow a;\left(b+1\right)\in U\left(3\right)=\left\{-1;1;-3;3\right\}\)
\(\Rightarrow\left(a;b\right)\in\left\{\left(-1;-4\right);\left(1;2\right);\left(-3;-2\right);\left(3;0\right)\right\}\)
b) \(2n+7⋮n+1\left(n\inℤ\right)\)
\(\Rightarrow2n+7-2\left(n+1\right)⋮n+1\)
\(\Rightarrow2n+7-2n-2⋮n+1\)
\(\Rightarrow5⋮n+1\)
\(\Rightarrow n+1\in U\left(5\right)=\left\{-1;1;-5;5\right\}\)
\(\Rightarrow n\in\left\{-2;0;-6;4\right\}\)
c) \(xy+x-y=6\left(x;y\inℤ\right)\)
\(\Rightarrow x\left(y+1\right)-y-1+1=6\)
\(\Rightarrow x\left(y+1\right)-\left(y+1\right)=5\)
\(\Rightarrow\left(x-1\right)\left(y+1\right)=5\)
\(\Rightarrow\left(x-1\right);\left(y+1\right)\in U\left(5\right)=\left\{-1;1;-5;5\right\}\)
\(\Rightarrow\left(x;y\right)\in\left\{\left(-0;-6\right);\left(2;4\right);\left(-4;-2\right);\left(6;0\right)\right\}\)
B= 3|x|+2/3|x|-1
Tìm x€Z để B đạt GTLN. Tìm GTLN của B
Tìm x€Z để B €N
a/ Cho M=\(\dfrac{\sqrt{x}-1}{2}\). Tìm x ∈ Z để M ∈ Z biết x<50
b/ Cho N=\(\dfrac{9}{\sqrt{x}-5}\). Tìm x ∈ Z để N ∈ Z
\(a,x< 50\Leftrightarrow\sqrt{x}-1< 5\sqrt{2}-1\\ M=\dfrac{\sqrt{x}-1}{2}\in Z\\ \Leftrightarrow\sqrt{x}-1\in B\left(2\right)=\left\{0;2;4;6\right\}\\ \Leftrightarrow\sqrt{x}\in\left\{1;3;5;7\right\}\\ \Leftrightarrow x\in\left\{1;9;25;49\right\}\\ b,\Leftrightarrow\sqrt{x}-5\inƯ\left(9\right)=\left\{-3;-1;1;3;9\right\}\left(\sqrt{x}-5>-5\right)\\ \Leftrightarrow\sqrt{x}\in\left\{2;4;6;8;14\right\}\\ \Leftrightarrow x\in\left\{4;16;36;64;196\right\}\)
Cho biểu thức A=\(\left(\dfrac{2-3x}{x^2+2x-3}-\dfrac{x+3}{1-x}-\dfrac{x+1}{x+3}\right):\dfrac{3x+12}{x^3-1}\)
và B=\(\dfrac{x^2+x-2}{x^3-1}\)
a Rút gọn biểu thức M=A.B
b Tìm x thuộc Z để M thuộc Z
c Tìm GTLN của biểu thức N=\(A^{-1}-B\)
a. \(A=\left(\dfrac{2-3x}{x^2+2x-3}-\dfrac{x+3}{1-x}-\dfrac{x+1}{x+3}\right):\dfrac{3x+12}{x^3-1}\left(ĐKXĐ:x\ne1;x\ne-3\right)\)
\(=\left(\dfrac{2-3x}{\left(x-1\right)\left(x+3\right)}+\dfrac{x+3}{x-1}-\dfrac{x+1}{x+3}\right):\dfrac{3x+12}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\left(\dfrac{2-3x}{\left(x-1\right)\left(x+3\right)}+\dfrac{\left(x+3\right)^2}{\left(x-1\right)\left(x+3\right)}-\dfrac{\left(x-1\right)\left(x+1\right)}{\left(x-1\right)\left(x+3\right)}\right):\dfrac{3x+12}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{2-3x+x^2+6x+9-x^2+1}{\left(x-1\right)\left(x+3\right)}:\dfrac{3x+12}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{3x+12}{\left(x-1\right)\left(x+3\right)}:\dfrac{3x+12}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{3x+12}{\left(x-1\right)\left(x+3\right)}.\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{3x+12}=\dfrac{x^2+x+1}{x+3}\)
\(M=A.B=\dfrac{x^2+x+1}{x+3}.\dfrac{x^2+x-2}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^2+x-2}{x+3}\)
b. -Để M thuộc Z thì:
\(\left(x^2+x-2\right)⋮\left(x+3\right)\)
\(\Rightarrow\left(x^2+3x-2x-6+4\right)⋮\left(x+3\right)\)
\(\Rightarrow\left[x\left(x+3\right)-2\left(x+3\right)+4\right]⋮\left(x+3\right)\)
\(\Rightarrow4⋮\left(x+3\right)\)
\(\Rightarrow x+3\in\left\{1;2;4;-1;-2;-4\right\}\)
\(\Rightarrow x\in\left\{-2;-1;1;-4;-5;-7\right\}\)
c. \(A^{-1}-B=\dfrac{x+3}{x^2+x+1}-\dfrac{x^2+x-2}{x^3-1}\)
\(=\dfrac{x+3}{x^2+x+1}-\dfrac{x^2+x-2}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{\left(x+3\right)\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}-\dfrac{x^2+x-2}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^2-x+3x-3-x^2-x+2}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x-1}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{1}{x^2+x+1}\)
\(=\dfrac{1}{x^2+2.\dfrac{1}{2}x+\dfrac{1}{4}+\dfrac{3}{4}}=\dfrac{1}{\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}}\le\dfrac{1}{\dfrac{3}{4}}=\dfrac{4}{3}\)
\(Max=\dfrac{4}{3}\Leftrightarrow x=\dfrac{-1}{2}\)
cho a=n+1/n-2
a)tìm n thuộc z để a thuộc z
b)tìm n thuộc z để a có GTLN
Ta có : \(\frac{n+1}{n-2}=\frac{n-2+3}{n-2}=1+\frac{3}{n-2}\)
a) Ta có 1 là số nguyên, để \(\frac{3}{n-2}\) là số nguyên thì 3 chia hết cho n - 2.
<=> n - 2 thuộc Ư(3) = {1;2;-1;-2}
=> n thuộc {3;4;1;0}
b) Để A lớn nhất thì n - 2 = 1 (nếu không có 1 thì những số lớn hơn 1)
=> n - 2 = 1
=> n = 3
Vậy GTLN của n = 3
a) A=\(\frac{n+1}{n-2}=1+\frac{3}{n-2}\)
muốn A nguyên thì n-3=Ư(3)={-1,-3,1,3}
n-2=-1=> n=1
n-2=1=> n=3
n-2=-3=> n=-1
n-2=3=> n=5
=> kl cvos 4 gtri n thỏa:....
b) A=1+\(\frac{3}{n-2}\)
=> muốn A lớn nhất thì \(\frac{3}{n-2}\)lớn nhất
có : \(\frac{3}{n-2}>=3\) khi n nguyên
=> dấu = dảy ra khi n=3
vậy GTLN A=1+3=4 khi x=3
a) Ta có: \(\frac{n+1}{n-2}=\frac{n-2+3}{n-2}=\frac{n-2}{n-2}+\frac{3}{n-2}=1+\frac{3}{n-2}\)
Để A là số nguyên thì 3 phải chia hết cho n - 2
=> n - 2 thuộc Ư(3) = { 1 ; 3 ; - 1 ; - 3 }
=> n thuộc { 3 ; 5 ; 1 ; - 1 }
Vậy n thuộc { 3 ; 5 ; 1 ; - 1 }
Cho \(A=\frac{n+1}{n-2}\)
a, Tìm n thuộc Z để A thuộc Z
b, Tìm n thuộc Z để A đạt GTLN
c, Tìm n thuộc Z để A đạt GTNN
a)
Để A thuộc Z thì ( dấu " : " là chia hết cho )
n + 1 : n - 2
n - 2 + 3 : n - 2
=> 3 : n - 2 => n - 2 thuộc Ư(3) = { 1; 3; -1; -3 }
Sau đó tìm n là xong
b) Cũng gần tương tự như phần a !
\(A=\frac{n+1}{n-2}=1+\frac{3}{n-2}\)
Để A nhỏ nhất thì \(\frac{3}{n-3}\)nhỏ nhất
mà n nguyên ( theo đề bài )
=> 3 : n - 3
Ta có bảng :
| n - 3 | 1 | -1 | 3 | -3 |
| n | 4 | 2 | 6 | 0 |
Lần lượt thay n vào A thì ta thấy A nhỏ nhất <=> n = 0
a) \(A=\frac{n+1}{n-2}=\frac{n-2+3}{n-2}=1+\frac{3}{n-2}\)
Để \(A\in Z\Leftrightarrow3⋮\left(n-2\right)\)
\(\Leftrightarrow n-2\inƯ\left(3\right)=\left\{1;-1;3;-3\right\}\)
Nêu n-2=1 thì n=3
Nếu n-2=-1 thì n=1
Nếu n-2=3 thì n=5
Nếu n-2=-3 thì n = -1
Vậy....
b) Để A đạt GTLN thì \(\frac{3}{x-2}\) đạt giá trị dương lớn nhất
=> x - 2 đạt giá trị dương nhỏ nhất
=> x - 2 = 1 => x = 3
Bài 244 :Tìm x thuộc z để :
a. 4n-5 chia hết cho n
b.-11 là bội của n-1
c. 2n-1 là ước của 3n+2
Bài 245 :Tìm n thuộc z để :
a.n^2-7 là bội của n+3
b.n+3 là bội của n^2-7
Bài 246 : Tìm x thuộc z sao cho :
n-1 là bội của n+5 và n+5 là bội của n-1
Cho A=\(\frac{n+1}{n-2}\)
a/ Tìm n thuộc Z để A thuộc Z
b/Tìm n thuộc Z để A có GTLN.
\(A=\frac{n+1}{n-2}\\ Athu\text{ộc}Zkhin+1⋮n-2\\ =>n-2+3⋮n-2\\ =>3⋮n-2\)
=>n-2 thuộc Ư(3)={1;3;-1;-3}
=>n thuoc {3;5;1;-1}
b) A có GTLN khi n lớn nhất =>n=5
Câu b không chắc chắn
VD13: Tìm GTLN và GTNN của:
b) N=3+4x/x^2+1
c) A=x^2-x+1/x^2+x+1
4) Cho x, y, z thuộc R thì x+y+z+xy+yz+zx=6. Tìm GTNN của A= x^2+y^2+z^2
5) Cho a, b, c thuộc R thỏa mãn: ab+bc+ca=5. Tìm min T=3a^2+3b^2+c^2