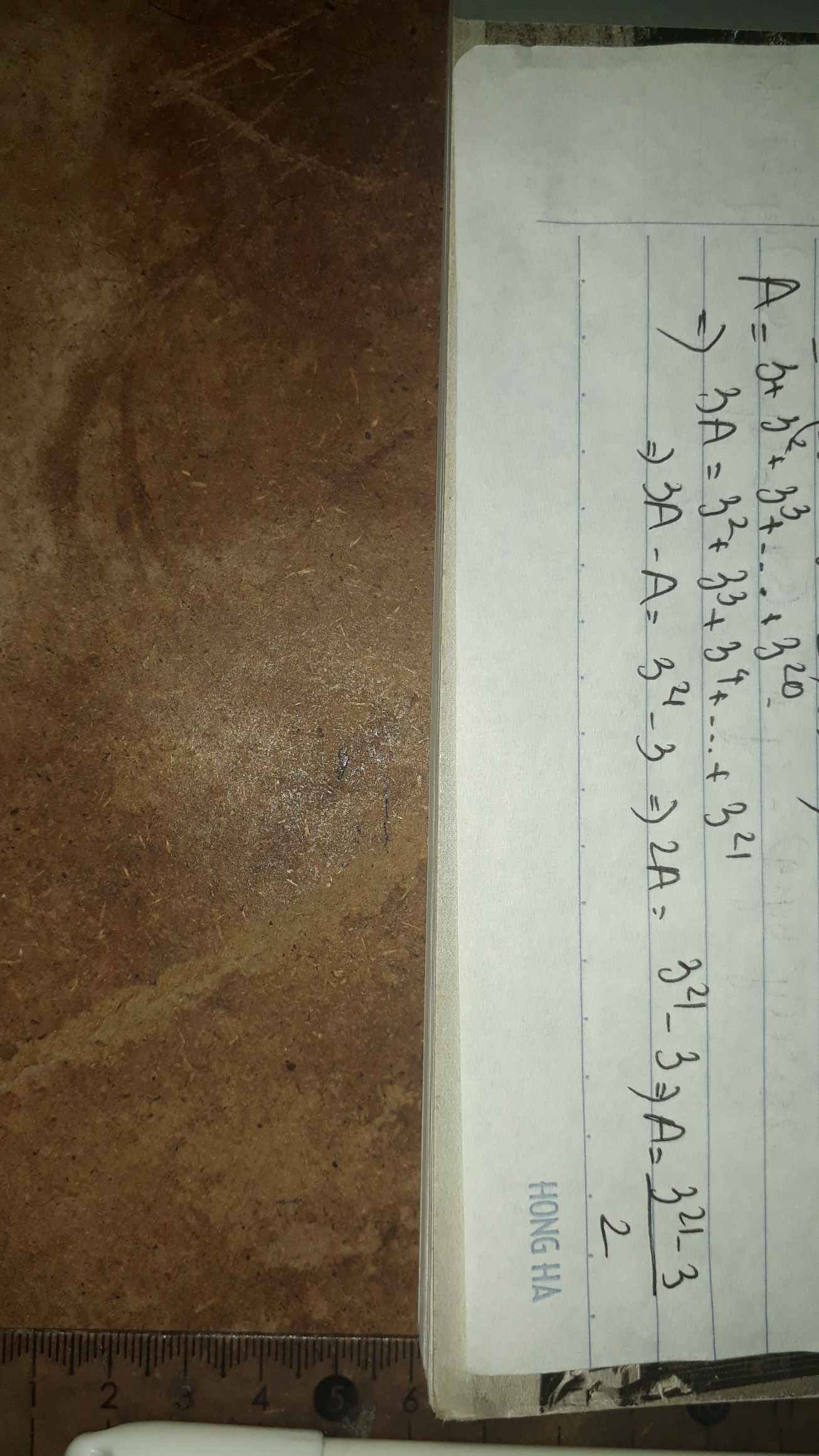1.

a.\(A=1+2^1+2^2+2^3+...+2^{2007}\)

\(2A=2+2^2+2^3+....+2^{2008}\)

b. \(A=\left(2+2^2+2^3+...+2^{2008}\right)-\left(1+2^1+2^2+..+2^{2007}\right)\)

\(=2^{2008}-1\) (bạn xem lại đề)

2.

\(A=1+3+3^1+3^2+...+3^7\)

a. \(2A=2+2.3+2.3^2+...+2.3^7\)

b.\(3A=3+3^2+3^3+...+3^8\)

\(2A=3^8-1\)

\(=>A=\dfrac{2^8-1}{2}\)

3

.\(B=1+3+3^2+..+3^{2006}\)

a. \(3B=3+3^2+3^3+...+3^{2007}\)

b. \(3B-B=2^{2007}-1\)

\(B=\dfrac{2^{2007}-1}{2}\)

4.

Sửa: \(C=1+4+4^2+4^3+4^4+4^5+4^6\)

a.\(4C=4+4^2+4^3+4^4+4^5+4^6+4^7\)

b.\(4C-C=4^7-1\)

\(C=\dfrac{4^7-1}{3}\)

5.

\(S=1+2+2^2+2^3+...+2^{2017}\)

\(2S=2+2^2+2^3+2^4+...+2^{2018}\)

\(S=2^{2018}-1\)

4:

a:Sửa đề: C=1+4+4^2+4^3+4^4+4^5+4^6

=>4*C=4+4^2+...+4^7

b: 4*C=4+4^2+...+4^7

C=1+4+...+4^6

=>3C=4^7-1

=>\(C=\dfrac{4^7-1}{3}\)

5:

2S=2+2^2+2^3+...+2^2018

=>2S-S=2^2018-1

=>S=2^2018-1

1) \(2^3\times x-5^2\times x=2\times\left(5^2+2^2\right)-33\)

\(x\times\left(2^3-5^2\right)=2\times\left(25+4\right)-33\)

\(x\times\left(8-25\right)=2\times29-33\)

\(x\times-17=25\)

\(x=-\dfrac{25}{17}\)

2) \(15\div\left(x+2\right)=\left(3^3+3\right)\div1\)

\(15\div\left(x+2\right)=\left(27+3\right)\div1\)

\(15\div\left(x+2\right)=30\div1\)

\(15\div\left(x+2\right)=30\)

\(x+2=\dfrac{1}{2}\)

\(x=-\dfrac{3}{2}\)

3) \(20\div\left(x+1\right)=\left(5^2+1\right)\div13\)

\(20\div\left(x+1\right)=\left(25+1\right)\div13\)

\(20\div\left(x+1\right)=26\div13\)

\(20\div\left(x+1\right)=2\)

\(x+1=20\div2\)

\(x+1=10\)

\(x=9\)

4) \(320\div\left(x-1\right)=\left(5^3-5^2\right)\div4+15\)

\(320\div\left(x-1\right)=\left(125-25\right)\div4+15\)

\(320\div\left(x-1\right)=100\div4+15\)

\(320\div\left(x-1\right)=25+15\)

\(320\div\left(x-1\right)=40\)

\(x-1=8\)

\(x=9\)

5) \(240\div\left(x-5\right)=2^2\times5^2-20\)

\(240\div\left(x-5\right)=4\times25-20\)

\(240\div\left(x-5\right)=100-20\)

\(240\div\left(x-5\right)=80\)

\(x-5=30\)

\(x=35\)

6) \(70\div\left(x-3\right)=\left(3^4-1\right)\div4-10\)

\(70\div\left(x-3\right)=\left(81-1\right)\div4-10\)

\(70\div\left(x-3\right)=80\div4-10\)

\(70\div\left(x-3\right)=20-10\)

\(70\div\left(x-3\right)=10\)

\(x-3=7\)

\(x=10\)

A= \(\frac{1}{3}+\frac{1}{15}+\frac{1}{35}+\frac{1}{35}+\frac{1}{99}=\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+\frac{1}{9.11}\)

\(2A=\frac{2}{1.3}+\frac{2}{3.5}+\frac{2}{5.6}+...+\frac{2}{9.11}\)

\(2A=1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+...+\frac{1}{9}-\frac{1}{11}\)

\(2A=1-\frac{1}{11}=\frac{10}{11}\)

\(A=\frac{10}{11}:2=\frac{5}{11}\)

\(D=\frac{3^2}{1.4}+\frac{3^2}{4.7}+...+\frac{3^2}{13.16}\)

\(D=3.\left(\frac{3}{1.4}+\frac{3}{4.7}+...+\frac{3}{13.16}\right)\)

\(D=3.\left(1-\frac{1}{4}+\frac{1}{4}-\frac{1}{7}+...+\frac{1}{13}-\frac{1}{16}\right)\)

\(D=3.\left(1-\frac{1}{16}\right)=3.\frac{15}{16}=2\frac{13}{16}\)

Ta có: \(A=3+3^2+3^3+...+3^{20}\)

\(\Leftrightarrow3\cdot A=3^2+3^3+3^4+...+3^{21}\)

\(\Leftrightarrow2\cdot A=3^{21}-3\)

hay \(A=\dfrac{3^{21}-3}{2}\)

xin lỗi bài trên của mình làm sai

Ta có: 3A = 3.(1+3+3²+3³+...+3⁹⁹+3¹⁰⁰⁾ 

3A = 3+3²+3³+...+3¹⁰⁰+3¹⁰¹

Suy ra: 3A – A = (3+3²+3³+...+3¹⁰⁰+3¹⁰¹)−(1+3+3²+3³+...+3⁹⁹+3¹⁰⁰)

2A = 3¹⁰¹−1

⇒ A = 3¹⁰¹−1

             2               

Vậy A = 3¹⁰¹−1

                 2           

em den lam

A=\(33.\dfrac{3-2}{3}.\dfrac{5-2}{5}....\dfrac{99-2}{99}\)

A=\(33.\dfrac{1}{3}.\dfrac{3}{5}.\dfrac{5}{7}...\dfrac{95}{97}.\dfrac{97}{99}\)

A=\(33.\dfrac{1}{99}=\dfrac{1}{3}\)

Dịch ra là: Ta có: 3A = 3. (1 + 3 + 32 + 33 + ... + 399 + 3100) (1 + 3 + 32 + 33 + ... + 399 + 3100) 3A = 3 + 32 + 33 + ... + 3100 + 31013 + 32 + 33 + ... + 3100 + 3101 Suy ra: 3A - A = (3 + 32 + 33 + ... + 3100 + 3101) - (1 + 3 + 32 + 33 + ... + 399 + 3100) (3 + 32 + 33 + ... + 3100 + 3101) - (1 + 3 + 32 + 33 + ... + 399 + 3100) ⇒⇒ A = 3101−123101−12 Vậy A = 3101−12

Mà đoạn 2A sai nhé bạn, sửa lại:

2A = 3101−13101−1 2A=-10001

A=-10001/2

A=-5000,5

Vậy A=-5000,5