Tính khoảng cách giữa hai điểm A và B trong mỗi trường hợp sau :
a) \(A\left(4;-1;1\right);B\left(2;1;0\right)\)
b) \(A\left(2;3;4\right);B\left(6;0;4\right)\)
Những câu hỏi liên quan
Tính khoảng cách giữa hai điểm A và B trong mỗi trường hợp sau: A(2; 3; 4), B(6; 0; 4)
Tính khoảng cách giữa hai điểm A và B trong mỗi trường hợp sau: A(4; -1; 1), B(2; 1; 0)
Cho tứ diện ABCD có ACADBCBD, ABa, CD
a
3
Khoảng cách giữa hai đường thẳng AB và CD bằng a . Tính khoảng cách h từ điểm cách đều 4 đỉnh A,B,C,D đến mỗi đỉnh đó A.
h
a
13
2
B.
h
a
13
4
C.
h
a...
Đọc tiếp
Cho tứ diện ABCD có AC=AD=BC=BD, AB=a, CD= a 3 Khoảng cách giữa hai đường thẳng AB và CD bằng a . Tính khoảng cách h từ điểm cách đều 4 đỉnh A,B,C,D đến mỗi đỉnh đó
A. h = a 13 2
B. h = a 13 4
C. h = a 3 2
D. h = a 3 4
Cho tứ diện ABCD có
A
B
A
D
B
C
B
D
,
A
B
a
,
C
D
a
30
. Khoảng cách giữa hai đường thẳng AB và CD bằng a. Tính khoảng cách h từ điểm cách đều 4 đỉnh A, B, C, D đến mỗi đỉnh đó. A.
h
a
13
2...
Đọc tiếp
Cho tứ diện ABCD có A B = A D = B C = B D , A B = a , C D = a 30 . Khoảng cách giữa hai đường thẳng AB và CD bằng a. Tính khoảng cách h từ điểm cách đều 4 đỉnh A, B, C, D đến mỗi đỉnh đó.
A. h = a 13 2
B. h = a 13 4
C. h = a 3 2
D. h = a 3 4
Chọn B
Gọi I là trung điểm AB, J là trung điểm CD
Từ AC=AD=BC=BD =>IJ chính là đoạn vuông góc chung của 2 đường thẳng AB và CD
=> IJ = a
Gọi O là điểm cách đều 4 đỉnh => O là tâm mặt cầu ngoại tiếp tứ diện ABCD
=> O nằm trên IJ => Ta cần tính OA
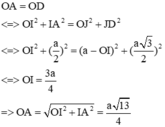
Ta có:
Đúng 0
Bình luận (0)
Để đo khoảng cách giữa hai điểm B và C trong đó B không tới được . Người ta xác định các điểm A, D,E như hình vẽ. Sau đó đo được khoảng cách giữa A và C là AC = 9m, Khoảng cách giữa D và C là DC= 6m khoảng cách giữa E và D là DE = 4m Khoảng các giữa hai điểm B và C là bao nhiêu
cho a, b thuộc Z. Gọi d là khoảng cách giữa hai điểm a và b trên trục số. Hãy so sánh d với b - a trong các trường hợp sau:
a = 12, b = 19 a = -3, b = +11a = -7, b = 6 a = -14, b = -5
Hai điện tích điểm q1 4
μ
C và q2 - 9
μ
C đặt tại hai điểm A và B cách nhau 9cm trong chân không. Điểm M có cường độ điện trường tổng hợp bằng O cách B một khoảng A. 18cm B. 9cm C. 27cm D. 4,5cm
Đọc tiếp
Hai điện tích điểm q1= 4 μ C và q2 = - 9 μ C đặt tại hai điểm A và B cách nhau 9cm trong chân không. Điểm M có cường độ điện trường tổng hợp bằng O cách B một khoảng
A. 18cm
B. 9cm
C. 27cm
D. 4,5cm
Đáp án: C
Để cường độ điện trường tại M bằng 0 thì hai vecto E 1 do q1 gây ra và E 2 do q2 gây ra phải ngược chiều và cùng độ lớn nên M nằm trên đường thẳng AB và ngoài đoạn AB
Do |q2| > |q1| nên r1 < r2 => r1 = r2 - AB,
=>
Đúng 0
Bình luận (0)
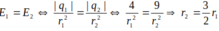
Cho elip (E) : \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\left(0< b< a\right)\). Tính tỉ số \(\dfrac{c}{a}\) trong các trường hợp sau :
a) Trục lớn bằng ba lần trục nhỏ
b) Đỉnh trên trục nhỏ nhìn hai tiêu điểm dưới một góc vuông
c) Khoảng cách giữa đỉnh trên trục nhỏ và đỉnh trên trục lớn bằng tiêu cự
Trong mặt phẳng tọa độ; cho 2 điểm A(1; 2) và B(4; 6). Tính khoảng cách giữa hai điểm đó.
A. 4
B. 2
C. 3
D. 5
