a) Vẽ hình vuông cạnh 4 cm.
b) Vẽ đường tròn ngoại tiếp hình vuông đó. Tính bán kinh R của đường tròn này.
c) Vẽ đường tròn nội tiếp hình vuông đó. Tính bán kính r của đường tròn này.
a) Vẽ hình vuông cạnh 4cm.
b) Vẽ đường tròn ngoại tiếp hình vuông đó. Tính bán kính R của đường tròn này.
c) Vẽ đường tròn nội tiếp hình vuông đó. Tính bán kính r của đường tròn này.
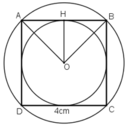
a) Vẽ hình vuông ABCD có cạnh 4cm.
b) Vẽ hai đường chéo AC và BD. Chúng cắt nhau tại O.
Đường tròn (O; OA) là đường tròn ngoại tiếp hình vuông ABCD.
Ta có:
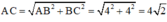 (cm)
(cm)
⇒ R = OA = AC/2 = 2√2 (cm).
c) Gọi H là trung điểm AB.
(O ; OH) là đường tròn nội tiếp hình vuông ABCD.
r = OH = AD/2 = 2cm.
a) Vẽ đường tròn tâm O, bán kính 2cm.
b) Vẽ hình vuông nội tiếp đường tròn (O) ở câu a).
c) Tính bán kính r của đường tròn nội tiếp hình vuông ở câu b) rồi vẽ đường tròn (O; r).
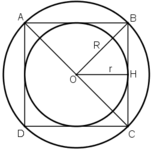
a) Chọn điểm O là tâm, mở compa có độ dài 2cm vẽ đường tròn tâm O, bán kính 2cm.
b) Vẽ đường kính AC và BD vuông góc với nhau. Nối A với B, B với C, C với D, D với A ta được tứ giác ABCD là hình vuông nội tiếp đường tròn (O; 2cm).
c) Vẽ OH ⊥ BC.
⇒ OH là khoảng cách từ từ tâm O đến BC
Vì AB = BC = CD = DA ( ABCD là hình vuông) nên khoảng cách từ tâm O đến AB, BC, CD, DA bằng nhau ( định lý lien hệ giữa dây cung và khoảng cách từ tâm đến dây)
⇒ O là tâm đường tròn nội tiếp hình vuông ABCD
OH là bán kính r của đường tròn nội tiếp hình vuông ABCD.
Tam giác vuông OBC có OH là đường trung tuyến ⇒ 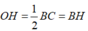
Xét tam giác vuông OHB có: r 2 + r 2 = O B 2 = 2 2 ⇒ 2 r 2 = 4 ⇒ r 2 = 2 ⇒ r = 2 ( cm )
Vẽ đường tròn (O; OH). Đường tròn này nội tiếp hình vuông, tiếp xúc bốn cạnh hình vuông tại các trung điểm của mỗi cạnh.
Kiến thức áp dụng
+ Đường tròn ngoại tiếp đa giác nếu đường tròn đó đi qua tất cả các đỉnh của đa giác. Khi đó ta nói đa giác nội tiếp đường tròn.
+ Đường tròn nội tiếp đa giác là đường tròn tiếp xúc với tất cả các cạnh của đa giác. Khi đó ta nói đa giác ngoại tiếp đường tròn.
a) Vẽ đường tròn tâm O, bán kính 2cm.
b) Vẽ hình vuông nội tiếp đường tròn (O) ở câu a.
c) Tính bán kính r của đường tròn nội tiếp hình vuông ở câu b) rồi vẽ đường tròn (O; r).
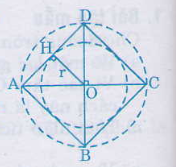
a) Chọn điểm O làm tâm , mở compa có độ dài 2cm vẽ đường tròn tâm O, bán kính 2cm: (O; 2cm)
Vẽ bằng eke và thước thẳng.
b) Vẽ đường kính AC và BD vuông góc với nhau. Nối A với B, B với C, C với D, D với A ta được tứ giác ABCD là hình vuông nội tiếp đường tròn (O;2cm)
c) Vẽ OH ⊥ AD
OH là bán kính r của đường tròn nội tiếp hình vuông ABCD.
r = OH = AH.
r2 + r2 = OA2 = 22 => 2r2 = 4 => r = √2 (cm)
Vẽ đường tròn (O;√2cm). Đường tròn này nội tiếp hình vuông, tiếp xúc bốn cạnh hình vuông tại các trung điểm của mỗi cạnh
Tính bán kính r của đường tròn nội tiếp hình vuông ở câu b) rồi vẽ đường tròn (O; r).
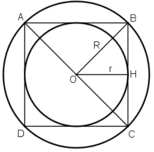
Vẽ OH ⊥ BC.
⇒ OH là khoảng cách từ từ tâm O đến BC
Vì AB = BC = CD = DA ( ABCD là hình vuông) nên khoảng cách từ tâm O đến AB, BC, CD, DA bằng nhau ( định lý lien hệ giữa dây cung và khoảng cách từ tâm đến dây)
⇒ O là tâm đường tròn nội tiếp hình vuông ABCD
OH là bán kính r của đường tròn nội tiếp hình vuông ABCD.
Tam giác vuông OBC có OH là đường trung tuyến ⇒ 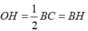
Xét tam giác vuông OHB có: r2 + r2 = OB2 = 22 ⇒ 2r2 = 4 ⇒ r2 = 2 ⇒ r = √2(cm)
Vẽ đường tròn (O; OH). Đường tròn này nội tiếp hình vuông, tiếp xúc bốn cạnh hình vuông tại các trung điểm của mỗi cạnh.
a) Vẽ một lục giác đều ABCDEG nội tiếp đường tròn bán kính 2cm rồi vé hình 12 cạnh đều AIBJCKDEMGN nội tiếp đường tròn đó. Nêu cách vẽ :
a) Tính độ dài cạnh AI
b) Tính bán kính r của đường tròn nội tiếp hình AIBJCKDEMGN
Hướng dẫn : Áp dụng các công thức ở bài 46
Cho tam giác ABC vuông tại A. Vẽ đường tròn ngoại tiếp bán kính R và nội tiếp bán kính r của tam giác đó. Biết R = 5cm; r = 2cm. Tính AB + AC.
Tam giác ABC vuông tại A => R=\(\frac{BC}{2}\) => BC=10
Ta có: r =\(\frac{2S}{AB+BC+AC}\) => \(\frac{AB.AC}{AB+AC+10}\) =2
AB2+AC2=100 (Pytago)
Giải pt ra, ta được: (AB;AC)=(6;8)
=> AB+AC=14
Cho đường tròn tâm (O), bán kính R ngoại tiếp đa giác dêdu của đường tròn A. Tính bán kính của đường tròn ngoại tiếp đa giác đó (A;R) trong trường hợp a, đa giác là tam giác đều b, đa giác là hình vuông c, đa giác là lục giác đều
Cho (O ; R), đường kính AB. Trên đường tròn lấy điểm C sao cho BC bằng R. Từ B vẽ tiếp tuyến với đường tròn, tiếp tuyến này cắt đường thẳng AC tại D
a, Cm tam giác ACB vuông tại C?
b, Tính AC , BD theo R.
c, Vẽ đường tròn ngoại tiếp tam giác CBD, gọi O' là tâm đường tròn này. Cm O'C là tiếp tuyến của (O) và AB là tiếp tuyến của (O').
d, Gọi I là tâm đường tròn nội tiếp tam giác ABD. Tính OI theo R.

a) Xét tam giác ACB, có CO là trung tuyến. Lại có \(CO=OA=OB=\frac{AB}{2}\), vậy nên tam giác ACB vuông lại C.
b) Xét tam giác vuông ACB, ta có:
\(\sin\widehat{CAB}=\frac{BC}{BA}=\frac{1}{2}\Rightarrow\widehat{CAB}=30^o\)
Xét tam giác vuông ACB, ta có:
\(cos\widehat{CAB}=\frac{AC}{AB}=\frac{\sqrt{3}}{2}\Rightarrow AC=R\sqrt{3}\)
Xét tam giác vuông ABD, ta có:
\(\tan\widehat{DAB}=\frac{BD}{AB}=\frac{\sqrt{3}}{3}\Rightarrow BD=\frac{2\sqrt{3}R}{3}\)
c) Ta thấy ngay tam giác BCD vuông tại C nên tâm đường tròn ngoại tiếp tam giác BCD là trung điểm cạnh huyền.
Vậy O' là trung điểm BD.
Xét tam giác OCO' và OBO' có:
O'C = O'B (gt)
OC = OB (= R)
OO' chung
\(\Rightarrow\Delta OCO'=\Delta OBO'\left(c-c-c\right)\)
\(\Rightarrow\widehat{O'CO}=\widehat{OBO'}=90^o\)
Vậy nên O'C là tiếp tuyến của đường tròn (O).
Lại có AB vuông góc với O'B tại B nên AB là tiếp tuyến tại B của đường tròn (O').
d) Gọi H là hình chiếu của I trên OB.
\(AD=\sqrt{AB^2+BD^2}=\frac{4R\sqrt{3}}{3}\)
Ta có hai công thức tính diện tích tam giác:
Công thức Hê-rông: \(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\) với a, b, c là độ dài các cạnh của tam giác, p là nửa chu vi
\(S=pr\) với r bán kính đường tròn nội tiếp.
Vậy nên \(r=\sqrt{\frac{\left(p-AB\right)\left(p-BD\right)\left(p-AD\right)}{p}}\)
\(p=\frac{AD+DB+BA}{2}=\left(1+\sqrt{3}\right)R\)
Vậy thì:
\(r=R\sqrt{\frac{4-2\sqrt{3}}{3}}=\frac{3-\sqrt{3}}{3}R\)
Thấy ngay IH = r.
Xét tam giác HIB có góc H vuông, \(\widehat{IBH}=45^o\) (Do BI là phân giác góc vuông)
Vậy nên \(IH=HB=\frac{3-\sqrt{3}}{3}R\)
\(\Rightarrow OH=R-HB=\frac{R\sqrt{3}}{3}\)
Xét tam giác vuông OIH, ta có:
\(OI=\sqrt{OH^2+IH^2}=R\sqrt{\frac{5-2\sqrt{3}}{3}}\)

a) Xét tam giác ACB, có CO là trung tuyến. Lại có \(CO=OA=OB=\frac{AB}{2}\), vậy nên tam giác ACB vuông lại C.
b) Xét tam giác vuông ACB, ta có:
\(\sin\widehat{CAB}=\frac{BC}{BA}=\frac{1}{2}\Rightarrow\widehat{CAB}=30^o\)
Xét tam giác vuông ACB, ta có:
\(cos\widehat{CAB}=\frac{AC}{AB}=\frac{\sqrt{3}}{2}\Rightarrow AC=R\sqrt{3}\)
Xét tam giác vuông ABD, ta có:
\(\tan\widehat{DAB}=\frac{BD}{AB}=\frac{\sqrt{3}}{3}\Rightarrow BD=\frac{2\sqrt{3}R}{3}\)
c) Ta thấy ngay tam giác BCD vuông tại C nên tâm đường tròn ngoại tiếp tam giác BCD là trung điểm cạnh huyền.
Vậy O' là trung điểm BD.
Xét tam giác OCO' và OBO' có:
O'C = O'B (gt)
OC = OB (= R)
OO' chung
\(\Rightarrow\Delta OCO'=\Delta OBO'\left(c-c-c\right)\)
\(\Rightarrow\widehat{O'CO}=\widehat{OBO'}=90^o\)
Vậy nên O'C là tiếp tuyến của đường tròn (O).
Lại có AB vuông góc với O'B tại B nên AB là tiếp tuyến tại B của đường tròn (O').
d) Gọi H là hình chiếu của I trên OB.
\(AD=\sqrt{AB^2+BD^2}=\frac{4R\sqrt{3}}{3}\)
Ta có hai công thức tính diện tích tam giác:
Công thức Hê-rông: \(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\) với a, b, c là độ dài các cạnh của tam giác, p là nửa chu vi
\(S=pr\) với r bán kính đường tròn nội tiếp.
Vậy nên \(r=\sqrt{\frac{\left(p-AB\right)\left(p-BD\right)\left(p-AD\right)}{p}}\)
\(p=\frac{AD+DB+BA}{2}=\left(1+\sqrt{3}\right)R\)
Vậy thì:
\(r=R\sqrt{\frac{4-2\sqrt{3}}{3}}=\frac{3-\sqrt{3}}{3}R\)
Thấy ngay IH = r.
Xét tam giác HIB có góc H vuông, \(\widehat{IBH}=45^o\) (Do BI là phân giác góc vuông)
Vậy nên \(IH=HB=\frac{3-\sqrt{3}}{3}R\)
\(\Rightarrow OH=R-HB=\frac{R\sqrt{3}}{3}\)
Xét tam giác vuông OIH, ta có:
\(OI=\sqrt{OH^2+IH^2}=R\sqrt{\frac{5-2\sqrt{3}}{3}}\)
Cho hình vẽ dưới đây trong đó A, B, C, D lần lượt là tâm của bốn đường tròn có bán kính bằng nhau, chúng tạo thành một hình vuông có cạnh là 4. Bốn đường tròn nhỏ bằng nhau và tâm của nó nằm trên các cạnh của hình vuông ABCD và mồi đường tròn này tiếp xúc với hai đường tròn lớn. Tìm diện tích lớn nhất của phần in đậm
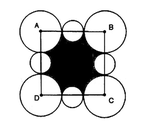
A. 5.38
B. 7.62
C. 5.98
D. 4.44