Cho tam giác ABC. Trên cạnh AB lấy hai điểm D và E sao cho AD=BE. Trên cạnh AC lấy hai diểm F và H sao cho AF=CH. Chứng minh rằng các tam giác BFH vàCDE có cùng một trọng tâm
Những câu hỏi liên quan
cho tam giác ABC trên cạnh AB lấy hai điểm D và E sao cho AD=BE Trên cạnh AC lấy hai điểm F và H sao cho AF=CH Chứng minh rằng các tam giác BFH và CDE có cùng một trọng tâm
: Cho tam giác ABC. Trên cạnh AB lấy hai điểm D và E sao cho AD = BE. Trên cạnh AC lấy hai điểm F và H sao cho AF = CH. Chứng minh rằng các tam giác BFH và CDE có cùng một trọng tâm.
Bạn tham khảo ak
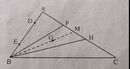
cho tam giác abc. trên AB, lấy điểm D và B sao cho AD=BE. Trên AC, lấy điềm và H sao cho AF=HC. C/m: tam giác BFH và tam giác CDE có cùng một trọng tâm.
Cho tam giác ABC. Trên cạnh AB lấy hai điểm D và E sao cho AD = BE. Trên cạnh AC lấy hai điểm F và H sao cho AF = CH. Chứng minh rằng các tam giác BFH và CDE có cùng một trọng tâm
Bạn tham khảo ak
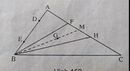
Cho tam giác ABC ,trên AB lấy D và E sao cho AD=BE.Trên AC lấy F và H sao cho AF=CH.Các đường trung tuyến AK, BN, CM của tam giác ABC cắt nhau tại G. HG cắt BF tại I.
a) I là trung điểm BF
b)Tam giác BFH và tam giác CDE có cùng trọng tâm
Cho tam giác ABC đều . Trên tia đối các tia AB , BC , CA lấy D , E , F sao cho AD = BE = CF . Chứng minh rằng : tam giác DEF đều . Tam giác ABC và tam giác DEF có cùng trọng tâm
Xét ΔDAF và ΔEBD có
DA=EB
góc DAF=góc EBD(=120 độ)
AF=BD
=>ΔDAF=ΔEBD
=>DF=ED
Xét ΔFCE và ΔEBD có
FC=EB
góc FCE=góc EBD
CE=BD
=>ΔFCE=ΔEBD
=>FE=ED
=>FE=ED=DF
=>ΔDEF đều
Đúng 2
Bình luận (0)
cho tam giác abc có ab = ac lấy điểm d trên cạnh ab , điểm e trên cạnh ac sao cho ad = ae
a, chứng minh rằng be =cd
b, gọi o là giao điểm của be và cd chứng minh rằng tam giác bod = tam giác coe .
a: Xét ΔAEB và ΔADC có
AE=AD
\(\widehat{DAC}\) chung
AB=AC
Do đó: ΔAEB=ΔADC
Suy ra: BE=CF
b: Ta có: AD+DB=AB
AE+EC=AC
mà AD=AE
và AB=AC
nên DB=EC
Xét ΔDBC và ΔECB có
DB=EC
\(\widehat{DBC}=\widehat{ECB}\)
BC chung
Do đó: ΔDBC=ΔECB
Suy ra: \(\widehat{ODB}=\widehat{OEC}\)
Xét ΔODB và ΔOEC có
\(\widehat{ODB}=\widehat{OEC}\)
BD=EC
\(\widehat{DBO}=\widehat{ECO}\)
Do đó: ΔODB=ΔOEC
Đúng 0
Bình luận (0)
Cho tam giác ABC . Có AB = AC . Lấy điểm D trên cạnh AB . Lấy điểm E trên cạnh AC sao cho AD = AE a) Chứng minh BE = CD b) Gọi O là giao điểm của BE và CD . Chứng minh rằng tam giác BOD bằng tam giác COE
Cho tam giác ABC nhọn có AB<AC.Kể tia phân giác AD của góc BAC ( D thuộc BC).Trên cạnh AC lấy điểm E sao cho AE =AB, trên tia AB lấy điểm F sao cho AF=AC
A) Chứng minh tam giác BDF= tam giác EDC.
B)Chứng minh ba điểm F,D,E thẳng hàng
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
Suy ra: DB=DE và \(\widehat{ABD}=\widehat{AED}\)
hay \(\widehat{DBF}=\widehat{DEC}\)
Xét ΔDBF và ΔDEC có
\(\widehat{DBF}=\widehat{DEC}\)
DB=DE
\(\widehat{BDF}=\widehat{EDC}\)
Do đó: ΔDBF=ΔDEC
Đúng 0
Bình luận (0)