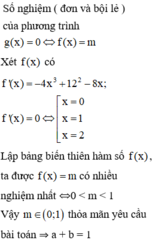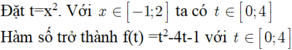Tìm giá trị lớn nhất hoặc nhỏ nhất của A = x4 + 4x3 +4x2 _ 8
Những câu hỏi liên quan
Cho hàm số y = f(x) = | x 4 - 4 x 3 + 4 x 2 + a |. Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên đoạn [0;2]. Số giá trị nguyên a thuộc đoạn [-3;3] sao cho M ≤ 2m là
A. 3
B. 5
C. 6
D. 7
Chọn B
Xét g(x) = x 4 - 4 x 3 + 4 x 2 + a với x ∈ [0;2]
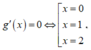
Bảng biến thiên g(x)
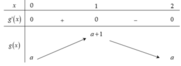
Trường hợp 1: a ≥ 0. Khi đó M = a + 1; m = a
Ta có M
≤
2m 
Với 
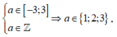
Trường hợp 2: 
Khi đó M = -a; m = -(a+1)
Trường hợp 3: -1 < a < 0. Với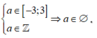 
Vậy có 5 giá trị a cần tìm.
Đúng 0
Bình luận (0)
Cho hàm số
f
x
x
4
−
4
x
3
+
4
x
2
+
a
. Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên đoạn [0;2]. Có bao nhiêu số nguyên a thuộc đoạn [-...
Đọc tiếp
Cho hàm số f x = x 4 − 4 x 3 + 4 x 2 + a . Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên đoạn [0;2]. Có bao nhiêu số nguyên a thuộc đoạn [-3;3] sao cho M ≤ 2 m ?
A. 3
B. 7
C. 6
D. 5
Cho hàm số
f
x
x
4
−
4
x
3
+
4
x
2
+
a
. Gọi
M
,
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên...
Đọc tiếp
Cho hàm số f x = x 4 − 4 x 3 + 4 x 2 + a . Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên 0 ; 2 . Có bao nhiêu số nguyên a thuộc − 4 ; 4 sao cho M ≤ 2 m
A. 7.
B. 5.
C. 6.
D. 4.
Đáp án A
Xét g x = x 4 − 4 x 3 + 4 x 2 + a
g ' x = 4 x 3 − 12 x 2 + 8 x = 0 ⇔ x = 0 , 1 , 2
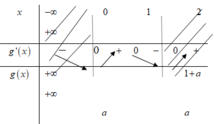
Đúng 0
Bình luận (0)
Cho hàm số
y
x
4
-
4
x
3
+
4
x
2
+
a
. Gọi M; m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn [0; 2] . Có bao nhiêu số nguyên a thuộc đoạn [ -3; 3] sao cho M≤ 2m? A....
Đọc tiếp
Cho hàm số y = x 4 - 4 x 3 + 4 x 2 + a . Gọi M; m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn [0; 2] . Có bao nhiêu số nguyên a thuộc đoạn [ -3; 3] sao cho M≤ 2m?
A. 4
B. 5
C. 6
D. 3
+ Xét hàm số y= x4- 4x3+ 4x2+ a trên đoạn [ 0; 2].
Ta có đạo hàm y’ = 4x3-12x2+ 8x,
y
'
=
0
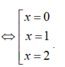
Khi đó; y( 0) = y( 2) = a; y( 1) = a+ 1
+ Nếu a≥ 0 thì M= a+ 1,m = a.
Để M ≤ 2m khi a≥ 1, suy ra a ∈ 1 ; 2 ; 3 thỏa mãn
+ Nếu a≤ - 1 thì M = a = - a , m = a + 1 = - a - 1 .
Để M≤ 2m thì a≤ -2, suy ra a a ∈ - 2 ; - 3
Vậy có 5 giá trị nguyên của a thỏa mãn yêu cầu.
Chọn B.
Đúng 0
Bình luận (0)
Cho hàm số f(x) |
x
4
-
4
x
3
+
4
x
2
+
a
|. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn [0;2]. Có bao nhiêu số nguyên a thuộc đoạn [-3;2] sao cho M
≤
2m? A. 7 B. 5 C. 6 D. 4
Đọc tiếp
Cho hàm số f(x) = | x 4 - 4 x 3 + 4 x 2 + a |. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn [0;2]. Có bao nhiêu số nguyên a thuộc đoạn [-3;2] sao cho M ≤ 2m?
A. 7
B. 5
C. 6
D. 4
Chọn D
Xét hàm số f(x) = x 4 - 4 x 3 + 4 x 2 + a trên đoạn [0;2], ta có:
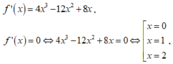
trên đoạn
Vì 
nên trên đoạn [0;2] giá trị lớn nhất và giá trị nhỏ nhất của hàm số 
lần lượt là a+1, a
Suy ra 
nếu 
nếu 
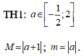
Khi đó 
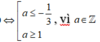
nên chọn 
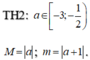
Khi đó 
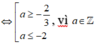nên chọn 
Vậy có 4 giá trị a thỏa yêu cầu
Đúng 0
Bình luận (0)
Cho hàm số
f
(
x
)
x
4
-
4
x
3
+
4
x
2
+
a
. Gọi M, m lần lượt là giá trị lớn nhất,...
Đọc tiếp
Cho hàm số f ( x ) = x 4 - 4 x 3 + 4 x 2 + a . Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên đoạn [0; 2] .Có bao nhiêu số nguyên a thuộc đoạn [-3; 3] sao cho M ≤ 2 m ?
A. 3
B. 7
C. 6
D. 5
Đáp án D
Xét hàm số 
.
;
Bảng biến thiên
Do 
nên 
suy ra 
.
Suy ra 
.
Nếu 
thì 
, 
.
Nếu 
thì 
, 
.
Do đó 
hoặc 
, do a nguyên và thuộc đoạn 
nên 
.
Đúng 0
Bình luận (0)
Cho hàm số
f
x
x
4
−
4
x
3
+
4
x
2
+
a
.
Gọi M, m lần lượt là các giá trị lớn nhất, nhỏ nhất của hàm số đã cho trên đoạn [ 0;2] Có bao nhiêu số nguyên a thuộc...
Đọc tiếp
Cho hàm số f x = x 4 − 4 x 3 + 4 x 2 + a . Gọi M, m lần lượt là các giá trị lớn nhất, nhỏ nhất của hàm số đã cho trên đoạn [ 0;2] Có bao nhiêu số nguyên a thuộc đoạn − 3 ; 3 sao cho M ≤ 2 m ?
A. 3
B. 7
C. 6
D. 5
Khi tham số
m
∈
a
;
b
thì hàm số
y
-
x
4
+
4
x
3
-
4
x
2
+
1
-...
Đọc tiếp
Khi tham số m ∈ a ; b thì hàm số y = - x 4 + 4 x 3 - 4 x 2 + 1 - m có số điểm cực trị là lớn nhất. Giá trị a + b bằng
A. 3
B. 0
C. 2
D. 1
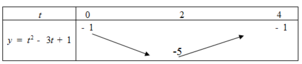
Tìm tích của giá trị lớn nhất và nhỏ nhất của hàm số y= x4-4x2-1 trên [ -1; 2].
A. 2
B. - 4
C. -5
D. 6
Tìm giá trị nhỏ nhất của biểu thức A= x4-4x3+7x2-12x+75
Lời giải:
$A=x^4-4x^3+7x^2-12x+75$
$=(x^2-2x)^2+3x^2-12x+75$
$=(x^2-2x)^2+3(x^2-4x+4)+63$
$=(x^2-2x)^2+3(x-2)^2+63\geq 63$
Vậy $A_{\min}=63$. Giá trị này đạt tại $x^2-2x=x-2=0$
$\Leftrightarrow x=2$
Đúng 0
Bình luận (0)