Áp dụng bất đẳng thức trong tam giác ABC:

=> CA+CB>AB;BA+BC>CA

Trong tam giác ABC kẻ AD sao cho AD _|_ BC ( D thuộc BC )

Xét tam giác ADC vuông tại D có :

Theo định lý Py-ta-go : AD2+DC2=AC2

=> DC > AC (1)

Xét tam giác ADB vuông tại D có :

Theo định lý Py-ta-go : AD2+DB2=AB2

=> DB<AB (2)

Từ (1) và (2) <=> DC+DB<AC+AB hay AB+AC>BC

ap dung bất đẳng thức tam giac

xét tam giac ABCcó CA+CB>AB

BA+BC>CA

Trong tam giác ABC kẻ AD sao cho AD _|_ BC ( D thuộc BC )

Xét tam giác ADC vuông tại D có :

Theo định lý Py-ta-go : AD²+DC²=AC²

=> DC > AC (1)

Xét tam giác ADB vuông tại D có :

Theo định lý Py-ta-go : AD²+DB²=AB²

=> DB<AB (2)

Từ (1) và (2) <=> DC+DB<AC+AB hay AB+AC>BC

Kẻ AH ⊥ BC

Xét ΔABH vuông tại H có:

∠AHB vuông, nên AB là cạnh lớn nhất

do đó: AB>BH (1)

Xét ΔACH vuông tại H có:

∠AHC vuông, nên AC là cạnh nhất

do đó: AC>CH (2)

Từ (1),(2) ta suy ra: AB+AC>BH+CH

Mà BH +CH=BC

nên AB+AC>BC

Giả sử BC là cạnh lớn nhất, ta suy ra:

AB<BC

AC<BC

Vậy AC+BC>AB; AB+BC>AC

\(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\) ; \(\overrightarrow{CB}+\overrightarrow{BA}=\overrightarrow{CA}\) ; \(\overrightarrow{AB}+\overrightarrow{CA}=\overrightarrow{CB}\)

\(\overrightarrow{BA}+\overrightarrow{CB}=\overrightarrow{CA}\) ; \(\overrightarrow{CB}-\overrightarrow{CA}=\overrightarrow{CB}+\overrightarrow{AC}=\overrightarrow{AB}\)

\(\overrightarrow{AB}-\overrightarrow{CA}=\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AM}\) (với M là trung điểm BC)

Trong 1 tam giác, tổng 2 cạnh bất kì luôn lớn hơn cạnh còn lại nên CA + CB> AB và BA + BC> CA

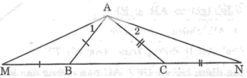
Trong ΔABC, ta có AC > AB

Suy ra: ∠(ABC) > ∠(ACB) (đối diện với cạnh lớn hơn là góc lớn hơn) (1)

Ta có: AB = BM (gt) ⇒ ΔABM cân tại B

Suy ra: ∠(AMB) = ∠A1(tính chất tam giác cân)

Trong ΔABM, ta có ∠(ABC) là góc ngoài tại đỉnh B

Suy ra: ∠(ABC) = ∠(AMB) + ∠A1 hay : ∠(ABC) = 2.∠(AMB)

Suy ra: ∠(AMB) = 1/2 ∠(ABC) (2)

Lại có: AC = CN (gt) ⇒ ΔACN cân tại C

Suy ra: ∠(ANC) = ∠A2(tính chất tam giác cân)

Trong ΔACN, ta có ∠(ACB) là góc ngoài tại đỉnh C

Suy ra: ∠(ACB) = ∠(ANC) + ∠A2 hay ∠(ACB) = 2∠(ANC)

Suy ra: ∠(ANC) = 1/2 ∠(ACB) (3)

Từ (1), (2) và (3) suy ra: ∠(AMB) > ∠(ANC) .

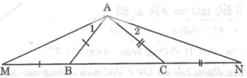
Trong ΔAMN, ta có: ∠(AMB) > ∠(ANC)

Suy ra: AN > AM (đối diện với góc lớn hơn là cạnh lớn hơn).