cho tam giác ABC vuông tại A, AH là đường cao, N là hình chiếu của H lên AC, AB=c,AC=b. Tính HN theo b,c

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A c/m hệ thức lượng trong tam giác vuông: h ²= b' × c' ( Trong đó AH là đường cao(h), BH là hình chiếu của AB lên BC (c'), CH là hình chiếu của AC lên BC (b')
Xem chi tiết
Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
góc HBA=góc HAC
=>ΔHBA đồng dạng với ΔHAC
=>HB/HA=HA/HC
=>HA^2=HB*HC
Đúng 0
Bình luận (0)
Cho tam giác abc vuông tại A có Ah là đường cao. Biết AB = 6cm, BC = 10cm:
a) Giải tam giác ABC
b) Gọi D là hình chiếu của H lên AC. Tính AH, AD
c) Kẻ AE vuông góc BD tại E. Chứng minh AB = AC.tanBEH
cho tam giác ABC vuông tại A, đường cao AH, biết AB = 6cm AC =8cm. a) CM: tam giác BAH đồng dạng với tam giác BCA. tính BC,BH b) gọi M là trung điểm của AB, N là hình chiếu của H trên AC. CM HN^2=CN*AN c) gọi I là giao điểm của MH và AC. CM CI*AB=2CN*MI
a: Xét ΔBAH vuông tại H và ΔBCA vuông tại A có
góc B chung
=>ΔBAH đồng dạng với ΔBCA
\(CB=\sqrt{6^2+8^2}=10\left(cm\right)\)
HB=6^2/10=3,6cm
b: ΔHAC vuông tại H có HN vuông góc AC
nên HN^2=NA*NC
Đúng 1
Bình luận (0)
cho tam giác abc vuông tại a đường cao ah gọi e và f lần lượt là hình chiếu của h trên ab và ac biết ab=c , ac=b
a) tính hb/hc theo c và b
b) tính be/cf theo c và b
a) Ta có: \(\dfrac{HB}{HC}=\dfrac{HB.HC}{HC^2}=\dfrac{HA^2}{HC^2}=\left(\dfrac{HA}{HC}\right)^2\)
Xét \(\Delta AHC\) và \(\Delta BAC:\) Ta có: \(\left\{{}\begin{matrix}\angle AHC=\angle BAC=90\\\angle ACBchung\end{matrix}\right.\)
\(\Rightarrow\Delta AHC\sim\Delta BAC\left(g-g\right)\Rightarrow\dfrac{HA}{HC}=\dfrac{AB}{AC}\)
\(\Rightarrow\dfrac{HB}{HC}=\left(\dfrac{AB}{AC}\right)^2=\dfrac{c^2}{b^2}\)
b) tham khảo ở đây:https://hoc24.vn/cau-hoi/cho-dabc-vuong-tai-a-duong-cao-ah-goi-e-f-lan-luot-la-cac-hinh-chieu-cua-h-tren-ab-va-ac-cmra-aeabaf.1150118751274
Đúng 2
Bình luận (0)
a) Áp dụng hệ thức lượng trong tam giác vuông có:
\(AB^2=BH.BC\)
\(AC^2=CH.CB\)
\(\Rightarrow\dfrac{BH}{CH}=\dfrac{AB^2}{AC^2}=\dfrac{c^2}{b^2}\)
b) Áp dụng hệ thức lượng trong tam giác vuông có:
\(BH^2=BE.BA\)
\(CH^2=CF.CA\)
\(\Rightarrow\dfrac{BH^2}{CH^2}=\dfrac{BE}{CF}.\dfrac{BA}{CA}\)\(\Leftrightarrow\dfrac{c^4}{b^4}=\dfrac{BE}{CF}.\dfrac{c}{b}\)
\(\Leftrightarrow\dfrac{BE}{CF}=\dfrac{c^3}{b^3}\)
Đúng 2
Bình luận (0)
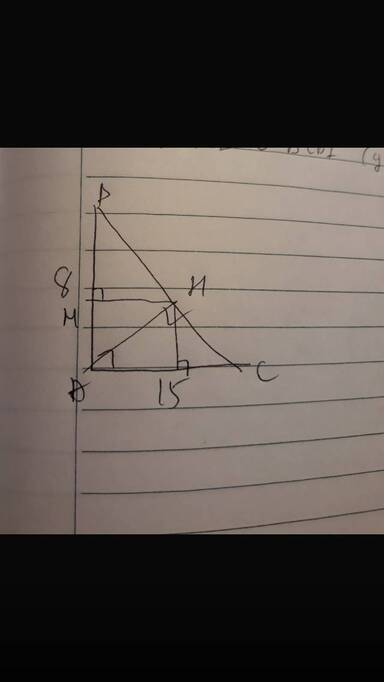
cho tam giác vuông ABC vuông ở A ; có AB = 8cm ; AC = 15cm ; đường cao AH
a) tính BC ; BH ; AH
b) gọi m,n lần lượt là hình chiếu của H lên AB và AC . tứ giác AMNH là hình gì ? tính độ dài đoạn MN
c) chứng minh AM.AB=AN.AC
Cho tam giác ABC vuông tại A, có AB= 8cm, Ac = 15cm, đường cao AH?
a, tính BC, BH, Ah
b, Gọi M,N lần lượt là hình chiếu của H lên AB và AC, AMNH là hình gì? tính đọ dài đoạn MN
c, chứng minh AM.AB=AN.AC
cho tam giác abc vuông tại a đường cao ah , biết ab/bc = 0,6 , ac=16cm
a. tính ab,ac,bc,hc
b. gọi m,n là hình chiếu của h lên ab,ac. cmr tam giác AMN và tam giác ABC đồng dạng
a: Xét ΔABC vuông tại A có sin C=AB/BC=3/5
=>cos C=căn 1-(3/5)^2=4/5
=>AC/BC=4/5
=>BC=20(cm)
\(AB=\sqrt{20^2-16^2}=12\left(cm\right)\)
ΔABC vuông tại A có AH là đường cao
nên CH*CB=CA^2
=>CH*20=16^2=256
=>CH=12,8(cm)
b: ΔHAB vuông tại H có HM là đường cao
nên AM*AB=AH^2
ΔHAC vuông tại H có HN là đường cao
nên AN*AC=AH^2
=>AM*AB=AN*AC
=>AM/AC=AN/AB
Xét ΔAMN vuông tại A và ΔACB vuông tại A có
AM/AC=AN/AB
Do đó: ΔAMN đồng dạng với ΔACB
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A đường cao Ah biết AB=12cm, AC=9cm tính Ah gọi M,N lần lượt là hình chiếu của H lên Ab và AC tính diện tích tứ giác BMNC.
a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
hay AH=7,2(cm)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A,đường cao AH. Gọi M,N lần lượt là hình chiếu vuông góc của H lên AB và AC. a, biết AC bằng 16 cm, sinCAH=4/5. Tính độ dài các cạnh BC,AB và cosB b,chứng minh AM x AB = AN x AC và tam giác ABC đồng dạng với tam giác AMN. c, chứng minh MA x MB + NA × NC=HB×HC d, Chứng minh S AMN/ S ABC=sin²B×sin²C
b: Xét ΔAHB vuông tại H có HM là đường cao ứng với cạnh huyền AB
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao ứng với cạnh huyền AC
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
Đúng 0
Bình luận (0)