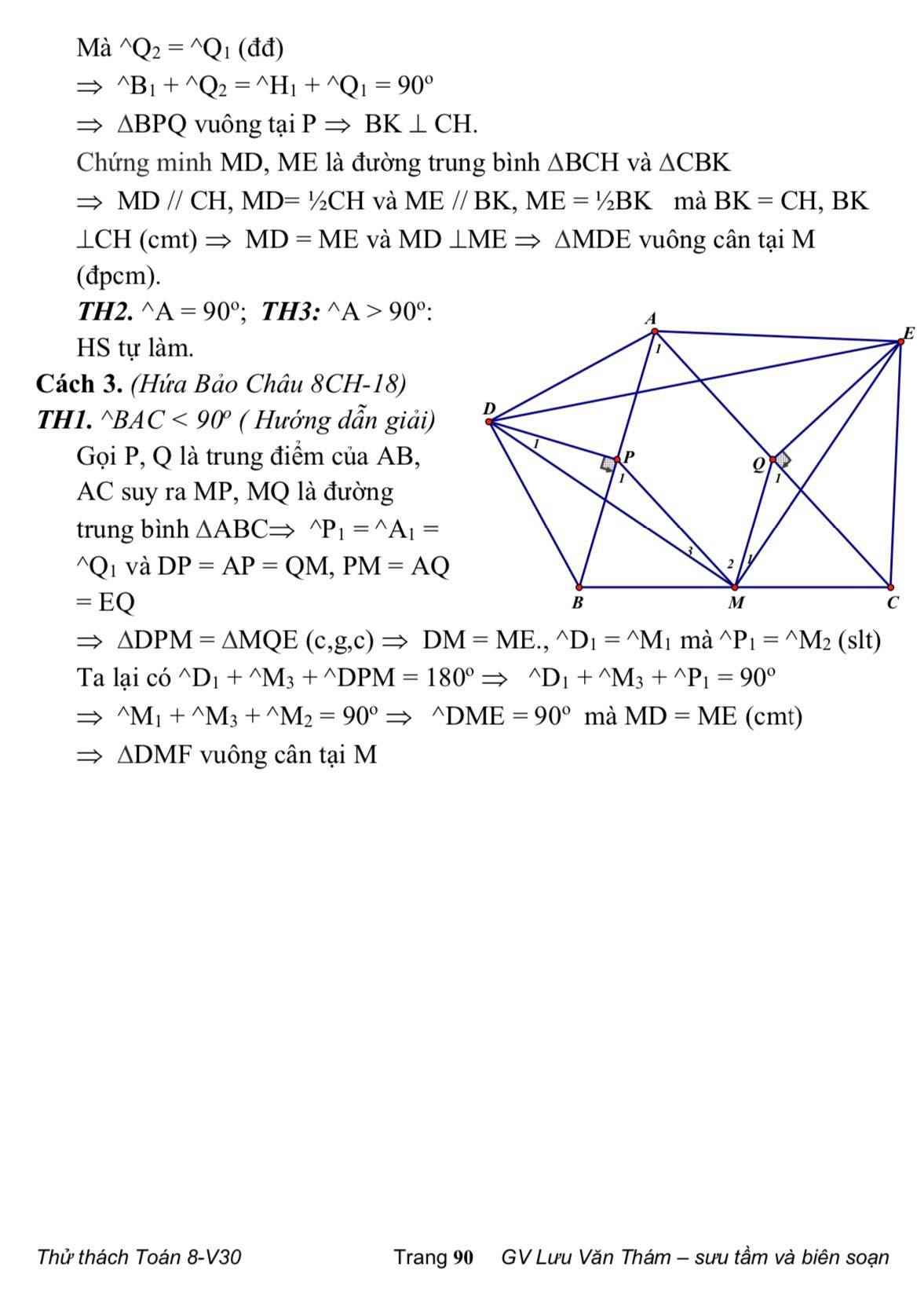
cho tam giác ABC cân tại A, BC =2cm. Vẽ tam giác vuông cân tại E (E và B # phía đối vs AC ), C/m rằng: AECB là hình thang vuông, tính các góc và các cạnh của nó

Những câu hỏi liên quan
Cho tam giác ABC vuông cân tại A , BC = 2cm . Ở phía ngoài tam giác ABC vẽ tam giác ACE vuông cân tại E
Tính các góc và các cạnh của hình thang AECB
Cho tam giác ABC vuông cân tại A, BC = 2cm. Ở phía ngoài tam giác ABC vẽ tam giác ACE vuông cân tại E
a) Chứng minh rằng AECB là hình thang vuông
b) Tính các góc và các cạnh của hình thang AECB
Bài 4: Cho tam giác ABC vuông cân tại A, BC2cm. Ở phía ngoài tam giác ABC vẽ tam giác ACE vuông cân tại E.
a) Chứng minh rằng EC vuông góc với BC
b) Tính số đo các góc của tứ giác ABCE.
Bài 5: Cho tam giác ABC vuông ở A, AH là đường cao, M là một điểm trên BC sao cho CMCA. Đường thẳng đi qua M song song với CA cắt AB tại I.
a) Chứng minh AM là phân giác của góc BAH
b) Chứng minh rằng luôn luôn có AB+AC AH+BC
Mình đang cần gấp bài này. Các bạn giúp mình nhé cảm ơn các bạn nhiều.
Đọc tiếp
Bài 4: Cho tam giác ABC vuông cân tại A, BC=2cm. Ở phía ngoài tam giác ABC vẽ tam giác ACE vuông cân tại E.
a) Chứng minh rằng EC vuông góc với BC
b) Tính số đo các góc của tứ giác ABCE.
Bài 5: Cho tam giác ABC vuông ở A, AH là đường cao, M là một điểm trên BC sao cho CM=CA. Đường thẳng đi qua M song song với CA cắt AB tại I.
a) Chứng minh AM là phân giác của góc BAH
b) Chứng minh rằng luôn luôn có AB+AC< AH+BC
Mình đang cần gấp bài này. Các bạn giúp mình nhé cảm ơn các bạn nhiều.
Bài 4:
a) Ta có tam giác ABC vuông cân tại A, nên góc BAC = 45 độ. Vì tam giác ACE vuông cân tại E, nên góc CAE = 45 độ. Từ đó suy ra góc CAE + góc BAC = 90 độ, tức là EC vuông góc với BC.
b) Vì tam giác ABC vuông cân tại A, nên góc BAC = 45 độ. Vì tam giác ACE vuông cân tại E, nên góc CAE = 45 độ. Từ đó suy ra góc BAE = góc BAC + góc CAE = 45 độ + 45 độ = 90 độ. Do đó, tứ giác ABCE là tứ giác vuông.
Bài 5:
a) Gọi K là giao điểm của đường thẳng AM và BH. Ta cần chứng minh góc BAK = góc CAK.
Vì CM = CA, ta có góc CMA = góc CAM. Vì đường thẳng AM song song với CA, nên góc CMA = góc KAB (do AB cắt đường thẳng AM tại I). Từ đó suy ra góc CAM = góc KAB.
Vì AH là đường cao, nên góc BAH = góc CAH. Từ đó suy ra góc BAK = góc CAK.
Vậy, AM là phân giác của góc BAH.
b) Ta có AB + AC = AB + AH + HC = BH + HC > BC (theo bất đẳng thức tam giác).
Vậy, luôn luôn có AB + AC < AH + BC.
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc A nhọn. Vẽ về phía ngoài tam giác ABC hai tam giác cân ABM, ACN vuông cân tại A. Gọi E là giao điểm của BN và CM. Cho MB = 3cm,, BC = 2cm, CN = 4cm. Tính MN.
a: Xét ΔABN và ΔAMC có
AB=AM
góc BAN=góc MAC
AN=AC
Do đó: ΔABN=ΔAMC
Gọi giao của ME với AB là D, NE với AC là F
góc AMD+góc MDA=90 độ
=>góc AMD+góc BDE=90 độ
=>góc DBE+góc BDE=90 độ
=>góc BED=90 độ
=>BN vuông góc với CM
b: BC^2+MN^2=BE^2+CE^2+ME^2+NE^2
=CN^2+BM^2
=>MN^2=7+5-3=9cm
=>MN=3cm
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc A nhọn. Vẽ về phía ngoài tam giác ABC hai tam giác cân ABM, ACN vuông cân tại A. Gọi E là giao điểm của BN và CM. Cho MB = 3cm,, BC = 2cm, CN = 4cm. Tính MN.
a: Xét ΔABN và ΔAMC có
AB=AM
góc BAN=góc MAC
AN=AC
Do đó: ΔABN=ΔAMC
Gọi giao của ME với AB là D, NE với AC là F
góc AMD+góc MDA=90 độ
=>góc AMD+góc BDE=90 độ
=>góc DBE+góc BDE=90 độ
=>góc BED=90 độ
=>BN vuông góc với CM
b: BC^2+MN^2=BE^2+CE^2+ME^2+NE^2
=CN^2+BM^2
=>MN^2=7+5-3=9cm
=>MN=3cm
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A , BC=2cm . Ở phía ngoài tam giác ABC vẽ tam giác ACE vuông cân tại E .
a) chứng minh rằng AECB là hình thang vuông
b) tính các góc và các cạnh của hình thang AECB
Cho tam giác ABC vuông tại A , BC=2cm . Ở phía ngoài tam giác ABC vẽ tam giác ACE vuông cân tại E .
a) chứng minh rằng AECB là hình thang vuông
b) tính các góc và các cạnh của hình thang AECB
Cho tam giác ABC vuông cân tại A, BC = 2 cm. Ở phía ngoài tam giác ABC, vẽ tam giác ACE vuông cân tại E. Tính các góc và các cạnh của hình thang AECB
∠ E = ∠ (ECB) = 90 0 , ∠ B = 45 0
∠ B + ∠ (EAB) = 180 0 (hai góc trong cùng phía bù nhau)
⇒ ∠ (EAB) = 180 0 - ∠ B = 180 0 – 45 0 = 135 0
Tam giác ABC vuông tại A. Theo định lí Py-ta-go ta có:
A B 2 + A C 2 = B C 2 mà AB = AC (gt)
⇒ 2 A B 2 = B C 2 = 2 2 = 4
A B 2 = 2 ⇒ AB= √2(cm) ⇒ AC = √2 (cm)
Tam giác AEC vuông tại E. Theo định lí Py-ta-go ta có:
E A 2 + E C 2 = A C 2 , mà EA = EC (gt)
⇒ 2 E A 2 = A C 2 = 2
E A 2 = 1
⇒ EA = 1(cm) ⇒ EC = 1(cm)
Đúng 0
Bình luận (0)
Cho tam giác ABC. Vẽ về phía ngoài tam giác ABC hai tam giác vuông cân ABD và tam giác vuông cân ACE tại E và D. Gọi M là trung điểm của BC. Chứng minh rằng tam giác DME vuông cân tại M.