252. (5n)2=625
Tìm n
Tìm số nguyên dương n biết: 25 ≤ 5 n ≤ 625
Tìm số nguyên dương n, biết: 25< 5n < 625;
Từ đề bài suy ra 52 < 5n < 54, tìm được n = 3
Tìm số tự nhiên n biết :
a.3n= 27
b. 5n= 625
`@` `\text {Ans}`
`\downarrow`
`a.`
`3^n = 27` phải k c?
`3^n = 27`
`=> 3^n = 3^3`
`=> n=3`
Vậy, `n=3`
TH2 (đề):
`3n = 27`
`=> n = 27 \div 3`
`=> n=9`
Vậy, `n=9`
`b.`
TH1:
`5^n = 625`
`=> 5^n = 5^4`
`=> n = 4`
Vậy, `n=4`
TH2:
`5n = 625`
`=> n = 625 \div 5`
`=> n = 125`
Vậy, `n=125`
tìm số tự nhiên n biết rằng
3n=27
2n=625
12n=144
2n.16=128
5n:29=27
(2n+1)=27
3n=27<=>n=27:3=9(TM)
2n=625<=>n=625:2=32,5(KTM VÌ n LÀ SỐ TỰ NHIÊN)
12n=144<=>n=144:12=12(TM)
2n.16=128<=>n=128;16:2=4(TM)
5n:29=27<=>n=27X29:5=156,6((KTM VÌ n LÀ SỐ TỰ NHIÊN)
(2n+1)=27<=>2n=27-1<=>2n=26<=>n=26:2=13
bạn tự kết luân nha
TM:thỏa mãn
KTM không thỏa mãn
ủng hộ mk nha mk bị âm điểm
5n/25=625
5n/25=625
<=>5n/52=54
=>5n=54.52=54+2=56
=>n=6
\(5^n=625.25 \Leftrightarrow 5^n=5^4.5^2 \Leftrightarrow 5^n=5^6 \Leftrightarrow n=6\)
Ta có: \(\dfrac{5^n}{25}=625\)
\(\Leftrightarrow5^n=625\cdot25=5^4\cdot5^2=5^6\)
hay n=6
Đặt tính rồi tính :
426 + 252 625 + 72
749 − 215 618 − 103
Phương pháp giải:
- Đặt tính: Viết phép tính sao cho các chữ số cùng hàng đặt thẳng cột với nhau.
- Tính: Cộng hoặc trừ các số lần lượt theo thứ tự từ phải sang trái.
Lời giải chi tiết:
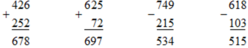
Tìm số tự nhiên n biết:
tìm số tự nhiên n a)625/5n=53; b)(-2n)/-128=4; c)5n=125; d)(3/7)n =81/2401 Cho biết 32<2n<512(n thuộc N) tìm giá trị của n Tìm x biết (x-1)4=161. a) 625/5n=53 => 5n=625/53=54/53=5 =>n=1
b) (-2n)/-128=4 =>-2n=4.(-128)=-2.256 =>n=256
c) (3/7)n=81/2401=(3/7)4 => n=4
2. 32<2n<512
<=> 25<2n<29
=> n=6;7;8
3. (x-1)4=16=24 => x-1=2 =>x=3
Tìm n
A ,5n= 625
B,6^2n = 1296
C,6^2n> 100
Đ, 25 <4n<100
A, \(5n=625\)
\(\Rightarrow n=625:5\)
\(\Rightarrow n=125\)
B, \(6^{2n}=1296\)
\(\Rightarrow6^{2n}=6^4\)
\(\Rightarrow2n=4\)
\(\Rightarrow n=2\)
C, \(6^{2n}>100\)
\(\Rightarrow\left(6^n\right)^2>10^2\)
\(\Rightarrow6^n>10\)
\(\Rightarrow n\ge2\) (mình không biết có đúng không)
Đ, \(25< 4n< 100\)
Vì \(4n⋮4\)
\(\Rightarrow4n\in\left\{28;32;36;...;92;96\right\}\)
\(\Rightarrow n\in\left\{7;8;9;...;23;24\right\}\)
Tìm giới hạn dãy số :
\(a,lim\dfrac{5n+1}{2n}\\ b,lim\dfrac{6n^2+8n+1}{5n^2+3}\\ c,lim\dfrac{3^n+2^n}{4.3^n}\\ d,lim\dfrac{\sqrt{n^2+5n+3}}{6n+2}\)
a: \(\lim\limits\dfrac{5n+1}{2n}=\lim\limits\dfrac{\dfrac{5n}{n}+\dfrac{1}{n}}{\dfrac{2n}{n}}=\lim\limits\dfrac{5+\dfrac{1}{n}}{2}=\dfrac{5+0}{2}=\dfrac{5}{2}\)
b: \(\lim\limits\dfrac{6n^2+8n+1}{5n^2+3}\)
\(=\lim\limits\dfrac{\dfrac{6n^2}{n^2}+\dfrac{8n}{n^2}+\dfrac{1}{n^2}}{\dfrac{5n^2}{n^2}+\dfrac{3}{n^2}}\)
\(=\lim\limits\dfrac{6+\dfrac{8}{n}+\dfrac{1}{n^2}}{5+\dfrac{3}{n^2}}\)
\(=\dfrac{6+0+0}{5+0}=\dfrac{6}{5}\)
c: \(\lim\limits\dfrac{3^n+2^n}{4\cdot3^n}\)
\(=\lim\limits\dfrac{\dfrac{3^n}{3^n}+\left(\dfrac{2}{3}\right)^n}{4\cdot\left(\dfrac{3^n}{3^n}\right)}\)
\(=\lim\limits\dfrac{1+\left(\dfrac{2}{3}\right)^n}{4}=\dfrac{1+0}{4}=\dfrac{1}{4}\)
d: \(\lim\limits\dfrac{\sqrt{n^2+5n+3}}{6n+2}\)
\(=\lim\limits\dfrac{\sqrt{\dfrac{n^2}{n^2}+\dfrac{5n}{n^2}+\dfrac{3}{n^2}}}{\dfrac{6n}{n}+\dfrac{2}{n}}\)
\(=\lim\limits\dfrac{\sqrt{1+\dfrac{5}{n}+\dfrac{3}{n^2}}}{6+\dfrac{2}{n}}\)
\(=\dfrac{\sqrt{1+0+0}}{6}=\dfrac{1}{6}\)
\(a,lim\dfrac{5n+1}{2n}=lim\dfrac{\dfrac{5n}{n}+\dfrac{1}{n}}{\dfrac{2n}{n}}=lim\dfrac{5+\dfrac{1}{n}}{2}=\dfrac{5}{2}\\ b,lim\dfrac{6n^2+8n+1}{5n^2+3}=lim\dfrac{\dfrac{6n^2}{n^2}+\dfrac{8n}{n^2}+\dfrac{1}{n^2}}{\dfrac{5n^2}{n^2}+\dfrac{3}{n^2}}=lim\dfrac{6+\dfrac{8}{n}+\dfrac{1}{n^2}}{5+\dfrac{3}{n^2}}=\dfrac{6}{5}\)
\(c,lim\dfrac{3^n+2^n}{4.3^n}=\dfrac{\dfrac{3^n}{3^n}+\dfrac{2^n}{3^n}}{\dfrac{4.3^n}{3^n}}=\dfrac{1+\left(\dfrac{2}{3}\right)^n}{4}=\dfrac{1}{4}\)
\(d,lim\dfrac{\sqrt{n^2+5n+3}}{6n+2}=lim\dfrac{\sqrt{\dfrac{n^2+5n+3}{n^2}}}{\dfrac{6n}{n}+\dfrac{2}{n}}=lim\dfrac{\sqrt{1+\dfrac{5}{n}+\dfrac{3}{n^2}}}{6+\dfrac{2}{n}}=\dfrac{1}{6}\)
\(a\text{)}lim\dfrac{5n+1}{2n}=lim\dfrac{5}{2}+lim\dfrac{1}{2n}=\dfrac{5}{2}\)
\(b\text{)}lim\dfrac{6n^2+8n+1}{5n^2+3}=lim\dfrac{6+\dfrac{8}{n}+\dfrac{1}{n^2}}{5+\dfrac{3}{n^2}}=\dfrac{6}{5}\)
\(c\text{)}lim\dfrac{3^n+2^n}{4.3^n}=lim\dfrac{\left(\dfrac{3}{3}\right)^n+\left(\dfrac{2}{3}\right)^n}{4}=\dfrac{1}{4}\)
\(d\text{)}lim\dfrac{\sqrt{n^2+5n+3}}{6n+2}=lim\dfrac{n\sqrt{1+\dfrac{5}{n}+\dfrac{3}{n^2}}}{n\left(6+\dfrac{2}{n}\right)}=lim\dfrac{\sqrt{1+\dfrac{5}{n}+\dfrac{3}{n^2}}}{6+\dfrac{2}{n}}=\dfrac{1}{6}\)