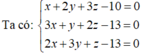tìm các số thực thỏa mãn 2x=3y=5z, x+2y+3z=300

Những câu hỏi liên quan
cho x,y,z là các số thực dương thỏa mãn \(x^2+y^2+z^2\ge\dfrac{1}{3}\)
chứng minh \(\dfrac{x^3}{2x+3y+5z}+\dfrac{y^3}{2y+3z+5x}+\dfrac{z^3}{2z+3x+5y}\ge\dfrac{1}{30}\)
đặt\(A=\dfrac{x^3}{2x+3y+5z}+\dfrac{y^3}{2y+3z+5x}+\dfrac{z^3}{2z+3x+5y}\)
\(=>A=\dfrac{x^4}{2x^2+3xy+5xz}+\dfrac{y^4}{2y^2+3yz+5xy}+\dfrac{z^4}{2z^2+3xz+5yz}\)
BBDT AM-GM
\(=>A\ge\dfrac{\left(x^2+y^2+z^2\right)^2}{2\left(x^2+y^2+z^2\right)+8\left(xy+yz+xz\right)}\)
theo BDT AM -GM ta chứng minh được \(xy+yz+xz\le x^2+y^2+z^2\)
vì \(x^2+y^2\ge2xy\)
\(y^2+z^2\ge2yz\)
\(x^2+z^2\ge2xz\)
\(=>2\left(x^2+y^2+z^2\right)\ge2\left(xy+yz+xz\right)< =>xy+yz+xz\le x^2+y^2+z^2\)
\(=>2\left(x^2+y^2+z^2\right)+8\left(xy+yz+xz\right)\le10\left(x^2+y^2+z^2\right)\)
\(=>A\ge\dfrac{\left(x^2+y^2+z^2\right)^2}{10\left(x^2+y^2+z^2\right)}=\dfrac{x^2+y^2+z^2}{10}=\dfrac{\dfrac{1}{3}}{10}=\dfrac{1}{30}\left(đpcm\right)\)
dấu"=" xảy ra<=>x=y=z=1/3
Đúng 1
Bình luận (0)
Cho x, y, z là các số thực thỏa mãn: 2x= 3y= 5z và |x-2y|= 5
Tìm giá trị lớn nhất của 3x - 2z
Câu hỏi của Phú Hồ Kim - Toán lớp 7 - Học toán với OnlineMath
tham khảo nhé
Đúng 0
Bình luận (0)
Cho các số thực dương x,y,z thỏa mãn:x^2+y^2+z^2≥1/3
CMR: x^3/2x+3y+5z + y^3/2y+3z+5x + z^3/2z+3x+5y ≥1/30
GIÚP GẤP
\(P=\dfrac{x^3}{2x+3y+5z}+\dfrac{y^3}{2y+3z+5x}+\dfrac{z^3}{2z+3x+5y}\)
\(P=\dfrac{x^4}{2x^2+3xy+5xz}+\dfrac{y^4}{2y^2+3yz+5xy}+\dfrac{z^4}{2z^2+3xz+5yz}\)
\(P\ge\dfrac{\left(x^2+y^2+z^2\right)^2}{2\left(x^2+y^2+z^2\right)+8\left(xy+yz+zx\right)}\ge\dfrac{\left(x^2+y^2+z^2\right)^2}{2\left(x^2+y^2+z^2\right)+8\left(x^2+y^2+z^2\right)}\)
\(P\ge\dfrac{x^2+y^2+z^2}{10}\ge\dfrac{1}{30}\)
\(P_{min}=\dfrac{1}{30}\) khi \(x=y=z=\dfrac{1}{3}\)
Đúng 1
Bình luận (0)
Cho x, y, z là các số thực thỏa mãn:
2x = 3y = 5z và |x - 2y| = 5.
Tìm giá trị lớn nhất của 3x – 2z.
Câu hỏi của Phú Hồ Kim - Toán lớp 7 - Học toán với OnlineMath
Tham khảo ơ link này nhé!
Đúng 0
Bình luận (0)
Tìm các số dương x,y,z thỏa mãn: \(\dfrac{3x-2y+z}{x}=\dfrac{3y-2z+x}{y}=\dfrac{3z-2x+y}{z}\)
Tìm các số x, y, z thoả mãn:
4x = 3y; 5z = 7x và x = 2y + 3z + 88
Cho x,y,z là các số thực dương thỏa mãn \(\frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{z+x}=12\)
Tìm GTLN của biểu thức \(P=\frac{1}{2x+3y+3z}+\frac{1}{3x+2y+3z}+\frac{1}{3x+3y+2z}\)
Má mày giúp tao bài tao gửi đii:(
Ta có bất đẳng thức: với \(x,y>0\)
\(\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}\)
Dấu \(=\)khi \(x=y\).
Áp dụng bất đẳng thức trên ta được:
\(\frac{1}{2x+3y+3z}\le\frac{1}{4}\left(\frac{1}{2x+y+z}+\frac{1}{2y+2z}\right)\le\frac{1}{4}\left[\frac{1}{4}\left(\frac{1}{x+y}+\frac{1}{x+z}\right)+\frac{1}{2}\left(\frac{1}{y+z}\right)\right]\)
\(=\frac{1}{16}\left(\frac{1}{x+y}+\frac{1}{x+z}\right)+\frac{1}{8}\left(\frac{1}{y+z}\right)\)
Tương tự với \(\frac{1}{3x+2y+3z},\frac{1}{3x+3y+2z}\)sau đó cộng lại vế với vế ta được:
\(P\le\frac{1}{4}\left(\frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{z+x}\right)=3\)
Dấu \(=\)xảy ra khi \(x=y=z=\frac{1}{8}\)
Cho ba số thực x, y, z thỏa mãn đồng thời các biểu thức:
x
+
2
y
+
3
z
-
10
0
,
3
x
+
y
+
2
z
-
13
0
và
2
x
+
3
y
+
z
-
13
0
. Tính
T
2
(
x
+
y
+
z
)
? A. T 1...
Đọc tiếp
Cho ba số thực x, y, z thỏa mãn đồng thời các biểu thức: x + 2 y + 3 z - 10 = 0 , 3 x + y + 2 z - 13 = 0 và 2 x + 3 y + z - 13 = 0 . Tính T = 2 ( x + y + z ) ?
A. T = 12
B. T = -12
C. T = -6
D. T = 6
Tìm số bộ số ( x;y;z ) thỏa mãn các điều kiện sau:
2
x
+
3
y
+
5
z
10
2
x
+
3
y
+
5
z
30
x
y
z
1
A. 1 B. 5 C. 6 D. 7
Đọc tiếp
Tìm số bộ số ( x;y;z ) thỏa mãn các điều kiện sau:
2 x + 3 y + 5 z = 10 2 x + 3 y + 5 z = 30 x y z = 1
A. 1
B. 5
C. 6
D. 7
Xét các bộ số ( x,y,z ) = log 2 a , log 3 b log 5 c trong đó a, b, c là hoán vị của { 2;3;5 }. Với các bộ số này thì điều kiện thứ ba của bài toán luôn được thỏa mãn.
Ta lại thấy
2 x + 3 y + 5 z = 2 log 2 a + 3 log 3 b + 5 log 5 c = a + b + c = 2 + 3 + 5 = 10
Và
2 x . 3 y . 5 z = 2 log 2 a . 3 log 3 b . 5 log 5 c = a b c = 2 . 3 . 5 = 30
Do đó các bộ xác định như trên luôn thỏa mãn các điều kiện đã cho. Do đó số các hoán vị của { 2;3;5 } là 3! = 6
Đáp án cần chọn là C
Đúng 0
Bình luận (0)