Tìm x, y để :
x2+45=y2
Những câu hỏi liên quan
Tìm các số nguyên tố x, y sao cho x2 + 45 = y2
Tham khảo:https://olm.vn/hoi-dap/detail/81346038854.html
Đúng 1
Bình luận (1)
Cho 2 đại lương tỉ lệ nghịch x và y x1 và x2 là hai giá trị của x y1 y2 là hai giá trị của y
A biết x1 × y1 = 45 x2 = 9 tìm y2
B biết x1=2 ; x2= 4 ; y1 + y2 = 12 tính y1 và y2
C biết x2 = 3 ; x1 + 2y2 = 18 ;y1=12 tìm x1, y2
Giúp với
rút gọn P=2/x-(x2/(x2-xy)+(x2-y2)/xy-y2/(y2-xy)):(x2-xy+y2)/(x-y)
r tìm gt P với |2x-1|=1 ; |y+1|=1/2
Bạn cần viết đề bằng công thức toán để được hỗ trợ tốt hơn.
Đúng 1
Bình luận (0)
Bài 2. Cho biết x và y là hai đại lượng tỉ lệ nghịch và x1 và x2 là hai giá trị bất kì của x; y1 và y2 là hai giá trị tương ứng của y. a)Biết x1y1 -45 và x2 9, tính y2; b)Biết x1 2; x2 4 và y1 + y2 -12, tính y1, y2; c)Biết x2 3, x1 + 2y2 18 và y1 12, tính x1, y2. CÁC BẠN GIÚP MÌNH NHANH VỚI
Đọc tiếp
Bài 2. Cho biết x và y là hai đại lượng tỉ lệ nghịch và x1 và x2 là hai giá trị bất kì của x; y1 và y2 là hai giá trị tương ứng của y.
a)Biết x1y1 = -45 và x2 = 9, tính y2;
b)Biết x1 = 2; x2 = 4 và y1 + y2 = -12, tính y1, y2; c
)Biết x2 = 3, x1 + 2y2 = 18 và y1 =12, tính x1, y2.
CÁC BẠN GIÚP MÌNH NHANH VỚI
Bài 2. Cho biết x và y là hai đại lượng tỉ lệ nghịch và x1 và x2 là hai giá trị bất kì của x; y1 và y2 là hai giá trị tương ứng của y. a)Biết x1y1 -45 và x2 9, tính y2; b)Biết x1 2; x2 4 và y1 + y2 -12, tính y1, y2; c)Biết x2 3, x1 + 2y2 18 và y1 12, tính x1, y2.
Đọc tiếp
Bài 2. Cho biết x và y là hai đại lượng tỉ lệ nghịch và x1 và x2 là hai giá trị bất kì của x; y1 và y2 là hai giá trị tương ứng của y.
a)Biết x1y1 = -45 và x2 = 9, tính y2;
b)Biết x1 = 2; x2 = 4 và y1 + y2 = -12, tính y1, y2;
c)Biết x2 = 3, x1 + 2y2 = 18 và y1 =12, tính x1, y2.
a)xvà y tỷ lệ nghịch với nhau nên ta có: x1 y1=x2.y2
=>x1. 12 = 3 . y 2
= > y 2 = 4 x 1
M à : x 1 + 2 y 2 = 18
= > x 1 + 2 . 4 x 1 = 18
= > 9 x 1 = 18 = > x 1 = 2
= > y 2 = 4 . 2 = 8
v ậ y x 1 = 2 ; y 2 = 8
Đúng 1
Bình luận (4)
cho x,y là hai đại lượng tỉ lệ nghịch.x,y là 2 giá trị khác nhau của x; y1; y2 là 2 giá trị tương ứng của y.
a) tính y2 biết x11y1=-45; x2=9
b) tính x1=2;x2=4;y1+y2=-12. tính y1,y2
c) x2=3;x1+2y2=18; y1=12. tính x1;y2
Cho x; y 0 thỏa mãn log2x + log2y log4( x + y) Tìm x; y để biểu thức P x2 + y2 đạt giá trị nhỏ nhất. A.
x
y
2
3
B.
x
2
3
;
y
2
C. x y 1 D.
y
2
3
;
x
2
2...
Đọc tiếp
Cho x; y > 0 thỏa mãn log2x + log2y = log4( x + y) Tìm x; y để biểu thức P = x2 + y2 đạt giá trị nhỏ nhất.
A. x = y = 2 3
B. x = 2 3 ; y = 2
C. x = y= 1
D. y = 2 3 ; x = 2 2 3
Chọn A.
Theo đầu bài ta có : 2log2xy = log2(x + y) hay x + y = (xy) 2
Đặt u = x + y và v = xy ta có điều kiện u2 - 4v ≥ 0 ; u > 0; v > 0.
Mà u = v2 nên v4 - 4v ≥ 0 suy ra 
Ta có P = v4 - 2v = g(v) với 
Đạo hàm g’(v) = 4v3-2 > 0 với mọi 
nên 
khi 
Đúng 0
Bình luận (0)
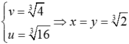
( 3x − y = 2m − 1
(x + 2y = 3m + 2.
hãy tìm m để hệ có nghiệm (x;y) thõa mãn x2 + y2 = 10.
\(\left\{{}\begin{matrix}3x-y=2m-1\\x+2y=3m+2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}6x-2y=4m-2\\x+2y=3m+2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}7x=7m\\x+2y=3m+2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=m\\y=\dfrac{3m+2-x}{2}=\dfrac{3m+2-m}{2}=m+1\end{matrix}\right.\)
\(x^2+y^2=10\)
\(\Leftrightarrow m^2+\left(m+1\right)^2=10\)
\(\Leftrightarrow2m^2+2m-9=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{-1+\sqrt{19}}{2}\\m=\dfrac{-1-\sqrt{19}}{2}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho biết x và y là 2 đại lượng tỉ lệ nghịch và x1,y1 là 2 giá trị bất kì của x ; x2,y2 là 2 giá trị tương ứng của y
a) biết x1×y1=-45 và x2=9. Tính y2
a) biết x1=2; x2=4 và y1+y2=-12. Tính y1,y2
c) biết x2=3; x1+2×y2=18; y1=12. Tính x1,y2
x và y đại lượng tỉ lệ nghịch
x1x2=y2y1hay x1 và x2 ta có:
23=y2y1⇒y13=y22
Mà y12+y22=52
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
y13=y22=y12+y2232+22=5213=4
⇒y13=4⇒y1=12
⇒y22=4⇒y2=8
Cho x; y 0 thỏa mãn log 2x+ log2ylog4(x+y) Tìm x; y để biểu thức P x2+y2 đạt giá trị nhỏ nhất. A.
x
y
2
3
B.
x
2
3
;
y
2
C. xy1 D.
y
2
3
;
x
2
2
3
Đọc tiếp
Cho x; y> 0 thỏa mãn log 2x+ log2y=log4(x+y) Tìm x; y để biểu thức P= x2+y2 đạt giá trị nhỏ nhất.
A. x = y = 2 3
B. x = 2 3 ; y = 2
C. x=y=1
D. y = 2 3 ; x = 2 2 3
Theo đầu bài ta có: log 2x+ log2y=log4(x+y) hay 2 log 2(xy) =log2(x+y)
Suy ra x+y=(xy) 2
Đặt u= x+ y; v= xy ta có điều kiện u2-4v≥0; u>0; v>0 .
Mà 
Ta có
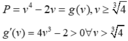
nên minP=
2
4
3
khi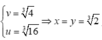 
Chọn A.
Đúng 0
Bình luận (0)