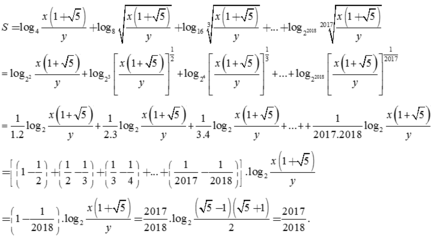Tính giá trị biểu thức C = 2x5 - 5y3 + 2015 tại x, y thỏa mãn |x - 1| + (y + 2)20 = 0

Những câu hỏi liên quan
Tính giá trị của biểu thức
\(C=2x^2-5y^3+2015\) tại x,y thỏa mãn \(|x-1|+\left(y+2\right)^{20}=0\)
Vì \(\left|x-1\right|\ge0\) và \(\left(y+2\right)^{20}\ge0\) nên \(\left|x-1\right|+\left(y+2\right)^{20}\ge0\)
Mà \(\left|x-1\right|+\left(y+2\right)^{20}=0\) ( đề bài cho )
\(\Rightarrow\)\(\left|x-1\right|=\left(y+2\right)^{20}=0\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}\left|x-1\right|=0\\\left(y+2\right)^{20}=0\end{cases}}\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}x-1=0\\y+2=0\end{cases}}\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}x=1\\y=-2\end{cases}}\)
Thay \(x=1;y=-2\) vàp biểu thức \(2x^2-5y^3+2015\) ta được :
\(2.1^2-5.\left(-2\right)^3+2015=2.1-5.\left(-8\right)+2015=2-\left(-40\right)+2015=42+2015=2057\)
Đúng 0
Bình luận (0)
Bài 1: Tính giá trị của biểu thức: x5 - 2009x4 + 2009x3 - 2009x2 + 2009x - 2010 tại x = 2008
Bài 2: Tính giá trị biểu thức 2x5 - 5x3 + 4 tại x, y thỏa mãn: (x - 1)20 + (y + 2)30 = 0
Bài 3: Tìm các cặp số nguyên (x, y) sao cho 2x - 5y + 5xy = 14
Bài 4: Chứng minh rằng đa thức P(x) = x3 - x + 5 không có nghiệm nguyên
Help ._.
cho x,y thỏa mãn đẳng thức 5x^2+5y^2+8xy-2x+2y+2=0
Tính giá trị biểu thức M=(x+y)^2015+(x-2)^2016+(y+1)^2017
kho....................wa..................troi.......................thi.....................ret.................lanh................wa..................tich............................ung.........................ho..............minh......................cho....................do....................lanh
Đúng 0
Bình luận (0)
Ta có: 5x2+5y2+8xy-2x+2y+2=0
=> 4x2+8xy+4y2+x2-2x+1+y2+2y+1=0
=> (2x+2y)2+(x-1)2+(y+1)2=0
=> {2x+2y=0 => x=-y
{x-1 = 0 => x=1
{y+1 =0 => y=-1
=> x=1, y=-1
Thay vào biểu thức M, ta có:
M=(1+-1)2015+(1-2)2016+(-1+1)2017=0+1+0=1 (đpcm)
Đúng 0
Bình luận (0)
cho x,y thỏa mãn đẳng thức 5x^2+5y^2+8xy-2x+2y+2=0
Tính giá trị biểu thức M=(x+y)^2015+(x-2)^2016+(y+1)^2017
giúp mình đi nha mình cần rất rất rất rất ...... gấp đấy !!!!=.='![]()
![]()
Đúng 0
Bình luận (2)
Xem thêm câu trả lời
Cho các số thực dương x,y thỏa mãn
log
9
x
log
12
y
log
16
x
+
y
. Tính giá trị của biểu thức
S
log
4
x
1
+
5...
Đọc tiếp
Cho các số thực dương x,y thỏa mãn log 9 x = log 12 y = log 16 x + y . Tính giá trị của biểu thức S = log 4 x 1 + 5 y + log 8 x 1 + 5 y + log 16 x 1 + 5 y 3 + .... + log 2 2018 x 1 + 5 y 2017
A. S = 2018 2017 .
B. S = 1 2017 .
C. S = 2017 2018 .
D. S = 1 2018 .
Cho các số thực dương x,y thỏa mãn
log
9
x
log
12
y
log
16
x
+
y
. Tính giá trị của biểu thức
S
log
4
x
1
+...
Đọc tiếp
Cho các số thực dương x,y thỏa mãn log 9 x = log 12 y = log 16 x + y . Tính giá trị của biểu thức S = log 4 x 1 + 5 y + log 8 x 1 + 5 y + log 16 x 1 + 5 y 3 + .... + log 2 2018 x 1 + 5 y 2017
A. S = 2018 2017 .
B. S = 1 2017 .
C. S = 2017 2018 .
D. S = 1 2018 .
Đáp án C
Đặt
log 9 x = log 12 y = log 16 x + y = t ⇒ x = 9 t y = 12 t x + y = 16 t ⇒ 9 t + 12 t = 16 t
⇔ 3 t 2 + 3 t .4 t − 4 t 2 = 0 *
Chia cả hai vế của phương trình (*) cho 4 t 2 ta được:
3 t 4 t 2 + 3 t 4 t − 1 = 0 ⇔ 3 t 4 t = 5 − 1 2 3 t 4 t = − 5 − 1 2 L ⇒ x y = 3 t 4 t = 5 − 1 2
Ta có:
S = log 4 x 1 + 5 y + log 8 x 1 + 5 y + log 16 x 1 + 5 y 3 + ... + log 2 2018 x 1 + 5 y 2017
= log 2 2 x 1 + 5 y + log 2 3 x 1 + 5 y 1 2 + log 2 4 x 1 + 5 y 1 3 + ... + log 2 2018 x 1 + 5 y 1 2017
= 1 1.2 log 2 x 1 + 5 y + 1 2.3 log 2 x 1 + 5 y + 1 3.4 log 2 x 1 + 5 y + ... + 1 2017.2018 log 2 x 1 + 5 y
= ( 1 − 1 2 + 1 2 − 1 3 + 1 3 − 1 4 + ... + 1 2017 − 1 2018 ) . log 2 x 1 + 5 y
= 1 − 1 2018 . log 2 x 1 + 5 y = 2017 2018 . log 2 5 − 1 5 + 1 2 = 2017 2018
Đúng 0
Bình luận (0)
Tính giá trị biểu thức : C = 2x5 - 5y3 + 2015 với x,y thõa mãn : |x - 1| + (y+2)20 = 0
|x-1| +(y+2)^20=0
|x-1| \(\ge0\)
(y+2)^20 \(\ge\)0
=> |x-1| +(y+2)^20\(\ge\) 0
"=" xảy ra khi x=1 y=-2
Với x=1 y=-2 thay vào tính C
Đúng 0
Bình luận (0)
1.Tính giá trị biểu thức: 6x^2+5x-2 tại x thõa mãn /x-2/=1
2.Tính giá trị biểu thức: 2x^8-3y^5+2 tại x,y thõa mãn (x+1)^20+(y+2)^26=0
3.Tính giá trị biểu thức: P=6x^3-4x^2y-14y^2+21xy+9 tại x,y thõa mãn 2x^2+7y=0
Mình đang cần gấp lắm ạ, mong mọi người giúp, mình cảm ơn nhiều ạ
Tính giá trị biểu thức 8x^2y+5x^3 tại x,y thỏa mãn:(x+1)^30+(y+2)^50=0
tính giá trị biểu thức sau:
M=3 mũ 2/2*5 + 3 mũ 2/5*8 + 3 mũ 2 /8*11 +....+ 3 mũ 2/98*101
Vì \(\left(x+1\right)^{30}+\left(y+2\right)^{50}\ge0\)mà theo đề bài ta có\(\left(x+1\right)^{30}+(y+2)^{50}=0\)
\(\Rightarrow\hept{\begin{cases}\left(x+1\right)^{30}=0\\\left(y+2\right)^{50}=0\end{cases}}\Rightarrow\hept{\begin{cases}x+1=0\\y+2=0\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=-1\\y=-2\end{cases}}\)
Vậy \(x=-1,y=-2\)