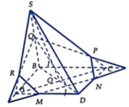
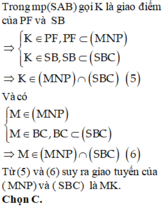Cho chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N là trung điểm AD, CD; I là điểm trên SO. Tìm thiết diện hình chóp với mặt phẳng (MNI) Mng kẻ hình và giải chi tiết giúp e với ạ, e cảm ơn

Những câu hỏi liên quan
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M,N,I lần lượt là trung điểm của AD,CD,SO. Tìm thiết diện của hình chóp S.ABCD với mặt phẳng (MNI)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. gọi M,N,P lần lượt là trung điểm của AD,CD,SB.
a) Tìm giao tuyến của (SAC) và (SBM). Tìm giao điểm I của SO và (MNP)
b) Xác định thiết diện của hình chóp S.ABCD cắt bởi (MNP)
Cho hình chóp S.ABCD đáy là hình bình hành tâm O. Gọi M, N, I là 3 điểm lấy trên AD, CD, SO. Thiết diện của hình chóp với mặt phẳng (MNI) là:
A. Một tam giác
B. Tứ giác
C. Ngũ giác
D. Lục giác
Cho hình chóp S.ABCD đáy là hình bình hành tâm O. Gọi M, N, I là 3 điểm lấy trên AD, CD, SO. Thiết diện của hình chóp với mặt phẳng (MNI) là:
A. Một tam giác
B. Tứ giác
C. Ngũ giác
D. Lục giác
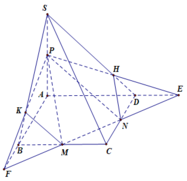
Đáp án C.
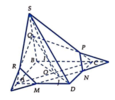
Trong (ABCD) gọi
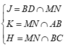
Trong (SBC) gọi: ![]()
Trong (SBD) gọi: Q = IJ ∩ SB
Trong (SBC) gọi: R = KQ ∩ SA
Suy ra, thiết diện là ngũ giác MNPQR.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình thang, AB // CD. Gọi M, N lần lượt là trung điểm của AD và BC; gọi G là trọng tâm tam giác SAB. Thiết diện của hình chóp với mặt phẳng (MNG) là hình bình hành thì A. AB 3CD B. AB 2CD C. CD 3AB D. CD 2AB
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang, AB // CD. Gọi M, N lần lượt là trung điểm của AD và BC; gọi G là trọng tâm tam giác SAB. Thiết diện của hình chóp với mặt phẳng (MNG) là hình bình hành thì
A. AB = 3CD
B. AB = 2CD
C. CD = 3AB
D. CD = 2AB
Cho hình chóp S.ABCD có đáy ABCD là hình thang, AB//CD. Gọi M, N lần lượt là trung điểm của AD và BC; gọi G là trọng tâm tam giác SAB. Thiết diện của hình chóp với mặt phẳng (MNG) là hình bình hành thì A. AB 3CD B. AB 2CD C. CD 3AB D. CD 2AB
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang, AB//CD. Gọi M, N lần lượt là trung điểm của AD và BC; gọi G là trọng tâm tam giác SAB. Thiết diện của hình chóp với mặt phẳng (MNG) là hình bình hành thì
A. AB = 3CD
B. AB = 2CD
C. CD = 3AB
D. CD = 2AB
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M; N’; P lần lượt là trung điểm của các cạnh BC; CD và SA. Gọi E là giao điểm của MN và AD; F là giao điểm của MN và AB. Tìm giao tuyến của (MNP) và (SBC)
A. ME
B. MH trong đó H là giao điểm của SD và PE
C. MK trong đó K là giao điểm của SB và PF
D. đáp án khác
Bài 3 : Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, M, N là trung điểm cạnh SC; SD
a) CMR: MN // (SAB); MM // (ABCD)
b) CMR: MO // (SAB)
Bài 4 :Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, M,N, P là trung điểm cạnh SA, SB, SC.
a) Chứng minh rằng : MN // (SCD).
b) Chứng minh rằng: MO // (SAB)
Giúp vs bạn !!
Cho hình chóp S.ABCD có đáy ABCD là hình thang có cạnh đáy AB và CD. Gọi M, N lần lượt là trung điểm của các cạnh AD, BC. G là trọng tâm của tam giác SAB. Thiết diện của hình chóp S.ABCD cắt bởi (IJG) là một tứ giác. Tìm điều kiện của AB,CD để thiết diện đó là hình bình hành? A. AB 3CD B. AB 2CD C. CD 2AB D. CD 3AB
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang có cạnh đáy AB và CD. Gọi M, N lần lượt là trung điểm của các cạnh AD, BC. G là trọng tâm của tam giác SAB. Thiết diện của hình chóp S.ABCD cắt bởi (IJG) là một tứ giác. Tìm điều kiện của AB,CD để thiết diện đó là hình bình hành?
A. AB = 3CD
B. AB = 2CD
C. CD = 2AB
D. CD = 3AB
Đáp án A
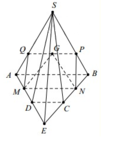
Qua G kẻ đường thẳng d song song với AB và cắt SA, SB lần lượt tại hai điểm Q, P. Vì MN là đường trung bình của ABCD ⇒ MN//AB
Do đó MN//PQ. Vậy giao tuyến của mặt phẳng (MNG) và (SAB) là PQ.
Mặt phẳng (MNG) cắt khối chóp S.ABCD theo thiết diện là tứ giác MNPQ
Vì MN//PQ suy ra MNPQ là hình thang
Để MNPQ là hình bình hành ⇔ MN=PQ (1)
Gọi I là trung điểm của AB, G là trọng tâm tam giác S A B ⇒ S G S I = 2 3
Tam giác SAB có P Q / / A B ⇒ P Q A B = S G S I = 2 3 ⇔ P Q = 2 3 A B (2)
Mà MN là đường trung bình hình thang A B C D ⇒ M N = A B + C D 2 (3)
Từ (1) , (2) và (3) suy ra 2 3 A B = A B + C D 2 ⇔ 4 A B = 3 A B + 3 C D ⇔ A B = 3 C D .
Đúng 1
Bình luận (0)